Study GuidesExam QuestionsPast Papers
AP®MathsCollege BoardCalculus BCStudy GuidesUnit 8: Applications of IntegrationVolumes of RevolutionWasher Method Around the x-Axis

Washer Method Around the x-Axis (College Board AP® Calculus BC): Study Guide

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

College Board Calculus BCCollege Board Calculus AB

Volume with washer method revolving around the x-axis

When should I use the washer method for a volume of revolution around the x-axis?

  • The washer method should be used when there is a gap between a region being rotated and the line it is being rotated around

  • For example, in the following diagram consider rotating the shaded area between the two curves around the x-axis

    • There would be a gap between the x-axis and the curve y subscript 1 equals f open parentheses x close parentheses

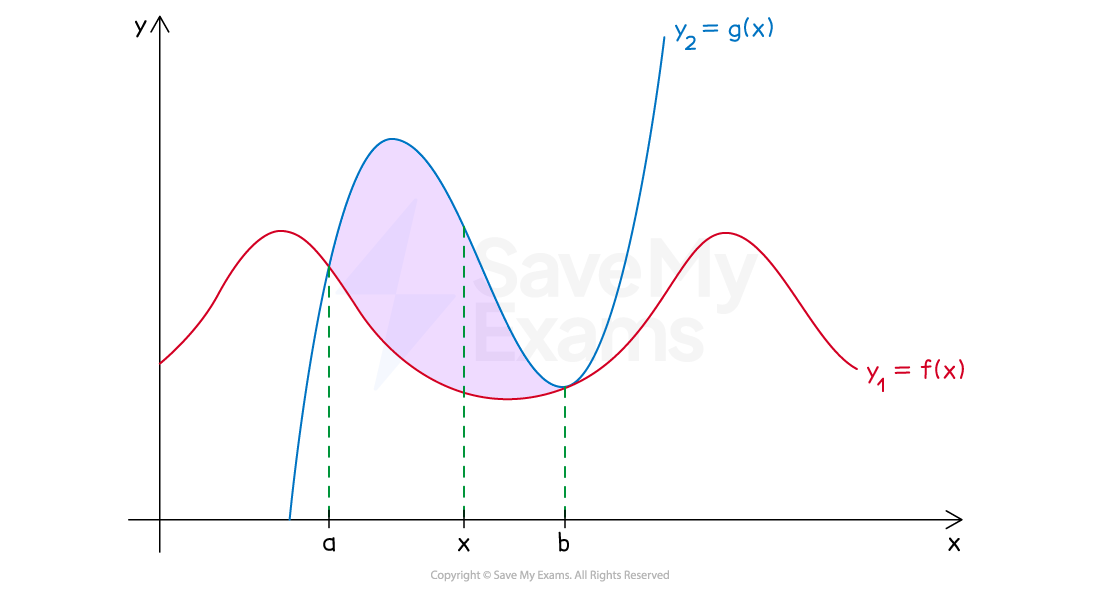
A graph showing a shaded region between the curves y_1=f(x) and y_2=g(x), and the lines x=a and x=b.

  • At a point x between a and b, the cross section of the solid of revolution would look like this:

A cross section of the solid of rotation following from the previous diagram

  • I.e., it would have the shape of a washer, with

    • Area equals pi open parentheses open parentheses g open parentheses x close parentheses close parentheses squared minus open parentheses f open parentheses x close parentheses close parentheses squared close parentheses

How can I use the washer method to calculate a volume of revolution around the x-axis?

  • Let f and g be continuous functions such that open vertical bar f open parentheses x close parentheses close vertical bar less than open vertical bar g open parentheses x close parentheses close vertical bar on the interval open square brackets a comma space b close square brackets

    • I.e. f open parentheses x close parentheses is closer to the x-axis than g open parentheses x close parentheses is on that interval

  • If the region bounded by

    • the curves y subscript 1 equals f open parentheses x close parentheses and y subscript 2 equals g open parentheses x close parentheses

    • between x equals a and x equals b

  • is rotated 2 pi radians left parenthesis 360 degree right parenthesis around the x-axis, then the volume of revolution is

    •  V equals integral subscript a superscript b pi open parentheses y subscript 2 squared minus y subscript 1 squared close parentheses space italic d x equals pi integral subscript a superscript b open parentheses y subscript 2 squared minus y subscript 1 squared close parentheses space italic d x

      • Note that y subscript 1 and y subscript 2 are both functions of x

  • Make sure that y subscript 2 is the curve further away from the x-axis

    • and y subscript 1 is the curve closer to the x-axis

      • If the curves 'swap places' over the interval

        • then split the calculation into separate integrals

  • If x equals a and x equals b are not stated in a question, these boundaries could involve

    • the y-axis (x equals 0)

    • and/or point(s) of intersection of the two curves

  • This method of finding volumes of revolution uses the idea of a definite integral as calculating an accumulation of change

    • It is a special case of 'finding volumes from areas of known cross-sections'

    • pi open parentheses y subscript 2 squared minus y subscript 1 squared close parentheses times increment x is the volume of a washer with

      • inner radius open vertical bar y subscript 1 close vertical bar

      • outer radius open vertical bar y subscript 2 close vertical bar

      • and length increment x

    • pi open parentheses y subscript 2 squared minus y subscript 1 squared close parentheses space d x is the limit of this volume element as increment x rightwards arrow 0

    • The integral integral subscript a superscript b pi open parentheses y subscript 2 squared minus y subscript 1 squared close parentheses space d x sums up all these infinitesimal volume elements between x equals a and x equals b

Examiner Tips and Tricks

Be careful not to confuse open parentheses y subscript 2 squared minus y subscript 1 squared close parentheses with open parentheses y subscript 2 minus y subscript 1 close parentheses squared

  • These are not equal!

    • open parentheses y subscript 2 minus y subscript 1 close parentheses squared equals y subscript 2 squared minus 2 y subscript 1 y subscript 2 plus y subscript 1 squared

Worked Example

Let R be the region enclosed by the graphs of f open parentheses x close parentheses equals 1 fourth x squared and g open parentheses x close parentheses equals x, as shown in the figure below.

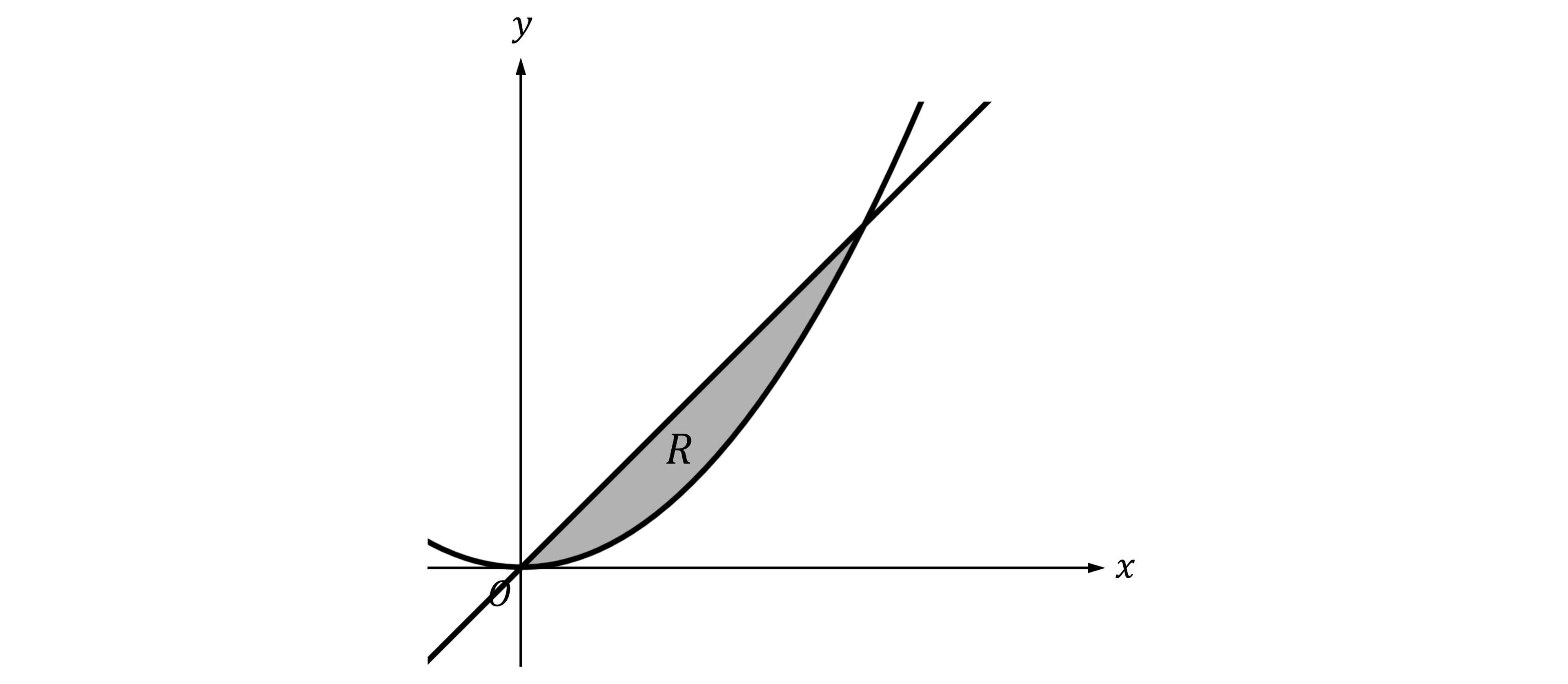
Graph showing a shaded region R enclosed by the curves y=x and y=x^2/4

Find the volume of the solid generated when R is rotated about the x-axis.

Answer:

Use V equals pi integral subscript a superscript b open parentheses y subscript 2 squared minus y subscript 1 squared close parentheses space italic d x

f open parentheses x close parentheses equals 1 fourth x squared is the function closest to the x-axis, so use y subscript 1 equals 1 fourth x squared and y subscript 2 equals x

To find a and b, solve f open parentheses x close parentheses equals g open parentheses x close parentheses to find the x-coordinates of the points of intersection of the two curves

table row cell 1 fourth x squared end cell equals x row cell x squared minus 4 x end cell equals 0 row cell x open parentheses x minus 4 close parentheses end cell equals 0 end table

table row x equals cell 0 space space or space space x equals 4 end cell end table

So a equals 0 and b equals 4

Set up and solve the integral

table row V equals cell pi integral subscript 0 superscript 4 open parentheses open parentheses x close parentheses squared minus open parentheses 1 fourth x squared close parentheses squared close parentheses space italic d x end cell row blank equals cell pi integral subscript 0 superscript 4 open parentheses x squared minus 1 over 16 x to the power of 4 close parentheses space italic d x end cell row blank equals cell pi open square brackets 1 third x cubed minus 1 over 80 x to the power of 5 close square brackets subscript 0 superscript 4 end cell row blank equals cell pi open parentheses open parentheses 1 third open parentheses 4 close parentheses cubed minus 1 over 80 open parentheses 4 close parentheses to the power of 5 close parentheses minus 0 close parentheses end cell row blank equals cell fraction numerator 128 pi over denominator 15 end fraction end cell row blank equals cell 26.808257... end cell end table

The question doesn't specify units, so the units of volume will be units cubed

26.808 units3 (to 3 decimal places)

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Did this page help you?

    Previous:Disc Method Around Other AxesNext:Washer Method Around the y-Axis
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.