Disc Method Around the y-Axis (College Board AP® Calculus BC) : Study Guide
Volume with disc method revolving around the y-axis
What is a volume of revolution around the y-axis?
This is very similar to a volume of revolution around the
-axis
A solid of revolution is formed when an area bounded by a function
(and other boundary equations) is rotatedradians
around the
-axis
The volume of revolution is the volume of this solid
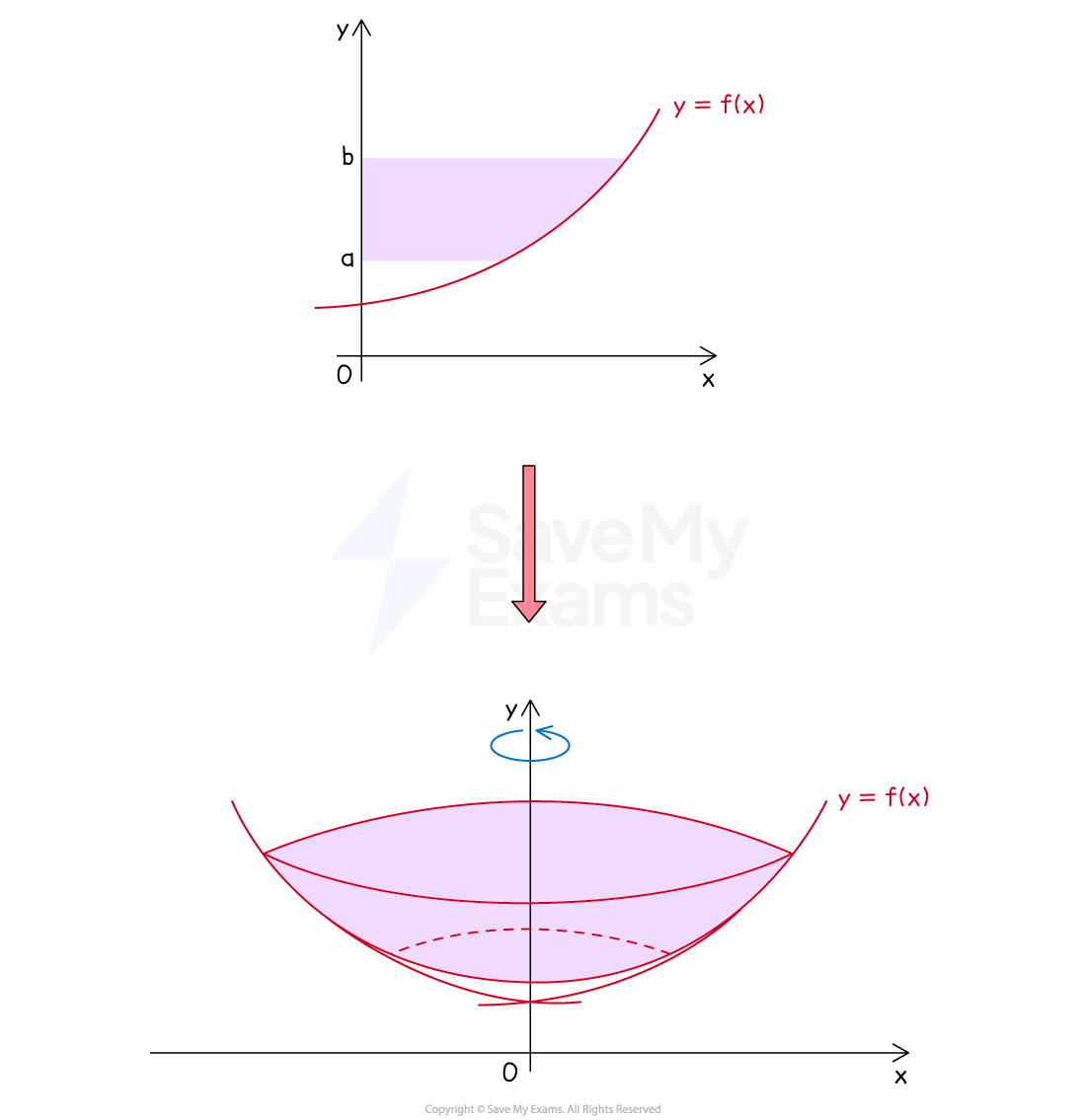
How can I use the disc method to calculate a volume of revolution around the y-axis?
For a continuous function
, if the region bounded by
the curve
and the
-axis
between
and
is rotated
radians
around the
-axis, then the volume of revolution is
Note that
here is a function of
This will mean rewriting
in the form
Also note that the integration is done with respect to
If
and
are not stated in a question, these boundaries could involve
the
-axis (
)
and/or a
-intercept of
Examiner Tips and Tricks
If the given function involves a square root, the problem may seem daunting
But the square root will be 'squared away' when using the Volume of Revolution formula
If a diagram is not provided, sketching the curve, limits, etc. can really help
A graphing calculator can help with this
Worked Example
Let be the region enclosed by the graph of
, the negative
-axis, and the positive
-axis, as shown in the figure below.
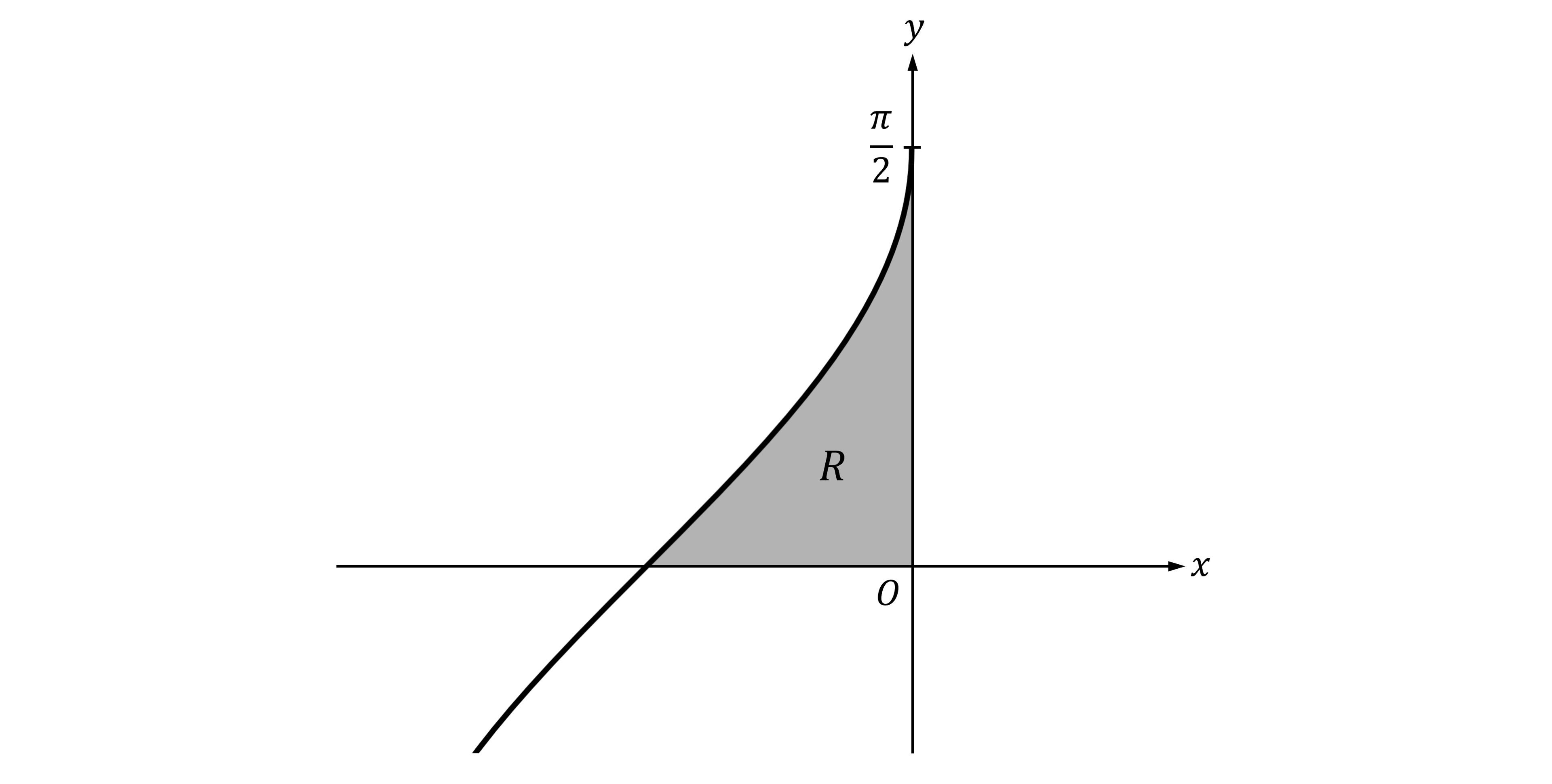
Find the volume of the solid generated when is rotated about the
-axis. Give your answer correct to 3 decimal places.
Answer:
Use
First rewrite the function as a function of
Now that can be put into the integral
Note that the integration will be along the -axis, from
to
The integral can be evaluated using your calculator
The question doesn't specify units, so the units of volume will be
0.280 units3 (to 3 decimal places)

You've read 0 of your 5 free study guides this week
Sign up now. It’s free!
Did this page help you?

