Study GuidesExam QuestionsPast Papers
AP®MathsCollege BoardCalculus BCStudy GuidesUnit 8: Applications of IntegrationVolumes of RevolutionDisc Method Around the x-Axis

Disc Method Around the x-Axis (College Board AP® Calculus BC): Study Guide

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Updated on

College Board Calculus BCCollege Board Calculus AB

Volume with disc method revolving around the x-axis

What is a volume of revolution around the x-axis?

  • A solid of revolution is formed when an area bounded by a function y equals f left parenthesis x right parenthesis
    (and other boundary equations) is rotated 2 pi radians left parenthesis 360 degree right parenthesis around the x-axis

  • The volume of revolution is the volume of this solid

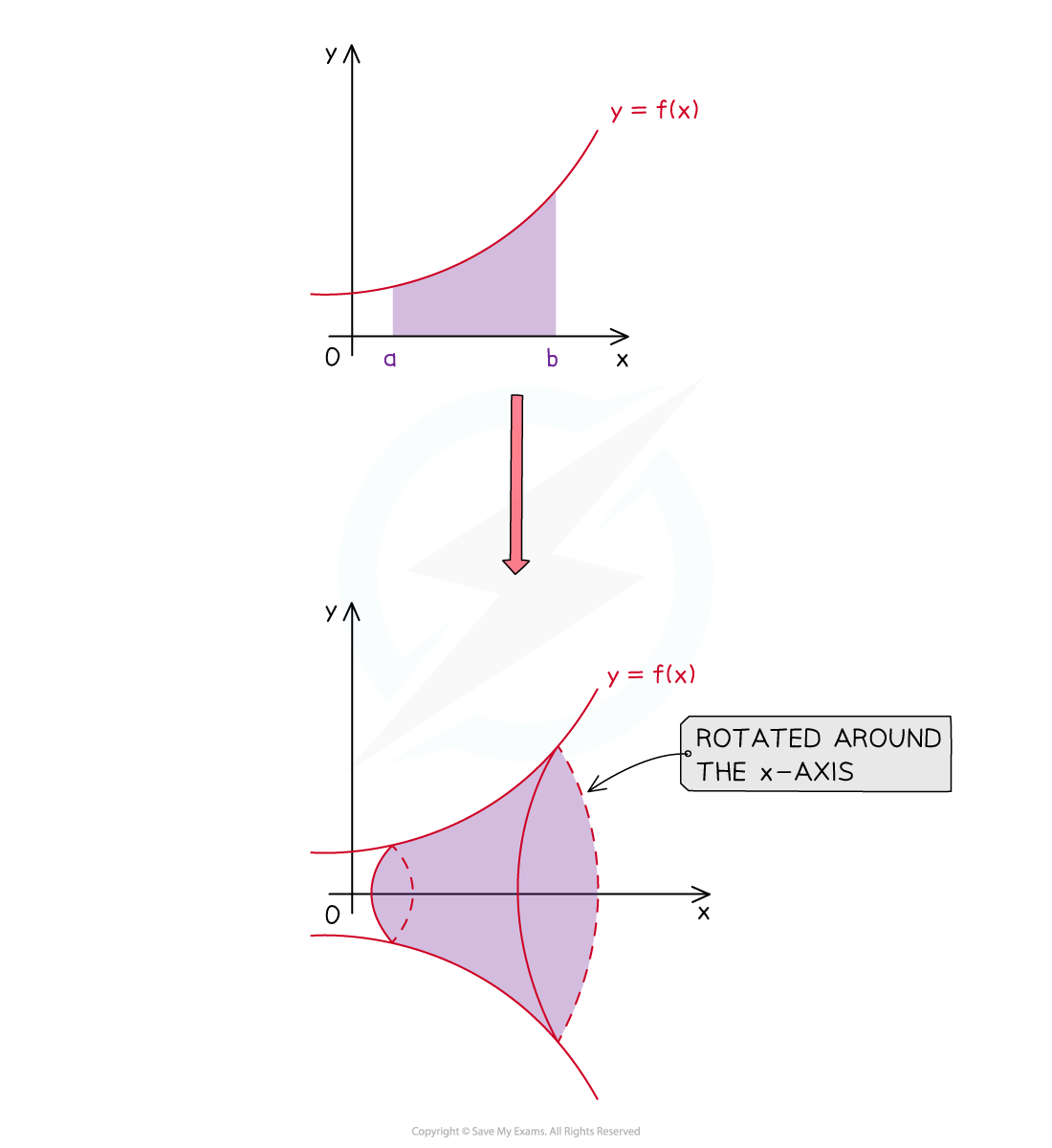
Example of a solid of revolution that is formed by rotating the area bounded by the function y=f(x), the lines x=a and x=b, and the x-axis about the x-axis

  • Be careful – the ’front’ and ‘back’ of this solid are flat

    • they were created from straight (vertical) lines

    • 3D sketches can be misleading

How can I use the disc method to calculate a volume of revolution around the x-axis?

  • For a continuous function f, if the region bounded by

    • the curve y equals f open parentheses x close parentheses and the x-axis

    • between x equals a and x equals b

  • is rotated 2 pi radians left parenthesis 360 degree right parenthesis around the x-axis, then the volume of revolution is

    •  V equals integral subscript a superscript b pi y squared space italic d x equals pi integral subscript a superscript b y squared space italic d x

      • Note that y is a function of x

  • If x equals a and x equals b are not stated in a question, these boundaries could involve

    • the y-axis (x equals 0)

    • and/or an x-intercept of y equals f left parenthesis x right parenthesis

  • This method of finding volumes of revolution uses the idea of a definite integral as calculating an accumulation of change

    • It is a special case of 'finding volumes from areas of known cross-sections'

    • pi y squared times increment x is the volume of a disc with

      • circular cross section of radius open vertical bar y close vertical bar

      • and length increment x

    • pi y squared space d x is the limit of this volume element as increment x rightwards arrow 0

    • The integral integral subscript a superscript b pi y squared space d x sums up all these infinitesimal volume elements between x equals a and x equals b

Examiner Tips and Tricks

If the given function involves a square root, the problem may seem daunting

  • But the square root will be 'squared away' when using the Volume of Revolution formula

If a diagram is not provided, sketching the curve, limits, etc. can really help

  • A graphing calculator can help with this

Worked Example

Let R be the region enclosed by the graph of f open parentheses x close parentheses equals square root of 3 x squared plus 2 end root, the x- and y-axes, and the vertical line x equals 3, as shown in the figure below.

Graph showing a shaded region R bounded by the curve y=sqrt(3x^2+2), the x- and y-axes, and the line x=3.

Find the volume of the solid generated when R is rotated about the x-axis.  Give your answer as an exact value.

Answer:

Use V equals pi integral subscript a superscript b y squared space italic d x

table row V equals cell pi integral subscript 0 superscript 3 open parentheses square root of 3 x squared plus 2 end root close parentheses squared space d x end cell row blank equals cell pi integral subscript 0 superscript 3 open parentheses 3 x squared plus 2 close parentheses space d x end cell row blank equals cell pi open square brackets x cubed plus 2 x close square brackets subscript 0 superscript 3 end cell row blank equals cell pi open square brackets open parentheses open parentheses 3 close parentheses cubed plus 2 open parentheses 3 close parentheses close parentheses minus 0 close square brackets end cell row blank equals cell 33 pi end cell end table

The question doesn't specify units, so the units of volume will be units cubed

33π units3

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Did this page help you?

    Previous:Semicircles as Cross SectionsNext:Disc Method Around the y-Axis
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.