AP®MathsCollege BoardCalculus BCRevision NotesUnit 8: Applications of IntegrationAreas & Arc LengthsArea Between Two Curves

Area Between Two Curves (College Board AP® Calculus BC): Revision Note

Written by: Jamie Wood

Reviewed by: Dan Finlay

Updated on 18 May 2026

Area between two curves in terms of x

How do I find the area between two curves?

Consider the diagram below where
- The area between two curves, $y = f (x)$ and $y = g (x)$ is being found
  - bounded by the lines $x = a$ and $x = b$
- This region is labeled $R$

Graph showing two curves, y = f(x) and y = g(x), with a shaded region R between x = a and x = b. Integral expression for the area R is displayed. — **Example of the area between two curves using vertical lines**

The region $R$ is the difference between the two areas found by:
- Integrating $y = f (x)$ between $x = a$ and $x = b$
- Integrating $y = g (x)$ between $x = a$ and $x = b$
As $f (x) \geq g (x)$ for all of this interval, this area can be calculated as
- $\int_{a}^{b} f (x) d x - \int_{a}^{b} g (x) d x$
This is equivalent to
- $\int_{a}^{b} (f (x) - g (x)) d x$
It is essential to have the function that is "above" the other be first inside the integral
- If the curves overlap and form multiple regions, see the method outlined in the 'Multiple Areas' study guide
Also note that if the graph of $y = f (x)$ is above the graph of $y = g (x)$ on $[a, b]$
- then $f (x) - g (x) \geq 0$ everywhere on that interval
- This means that you don't need to worry about negative integrals when integrating $\int_{a}^{b} (f (x) - g (x)) d x$
  - The integral will give the correct area value whether the area is above or below the $x$ -axis

What if I am not told the limits of integration?

If you are not told the limits, it is likely you are finding the area enclosed by two curves, $f (x)$ and $g (x)$ , which intersect each other
Find the $x$ -values of the points of intersection of the two curves by solving $f (x) = g (x)$
- These will be the limits for the integral

Examiner Tips and Tricks

In an FRQ, make sure you clearly state the integrand and the limits of integration.

Worked Example

Find the area of the region enclosed by the two curves with equations $y = 2 x^{2} - 4 x + 2$ and $y = - 2 x^{2} + 8 x - 6$ .

The curves are shown on the graph below.

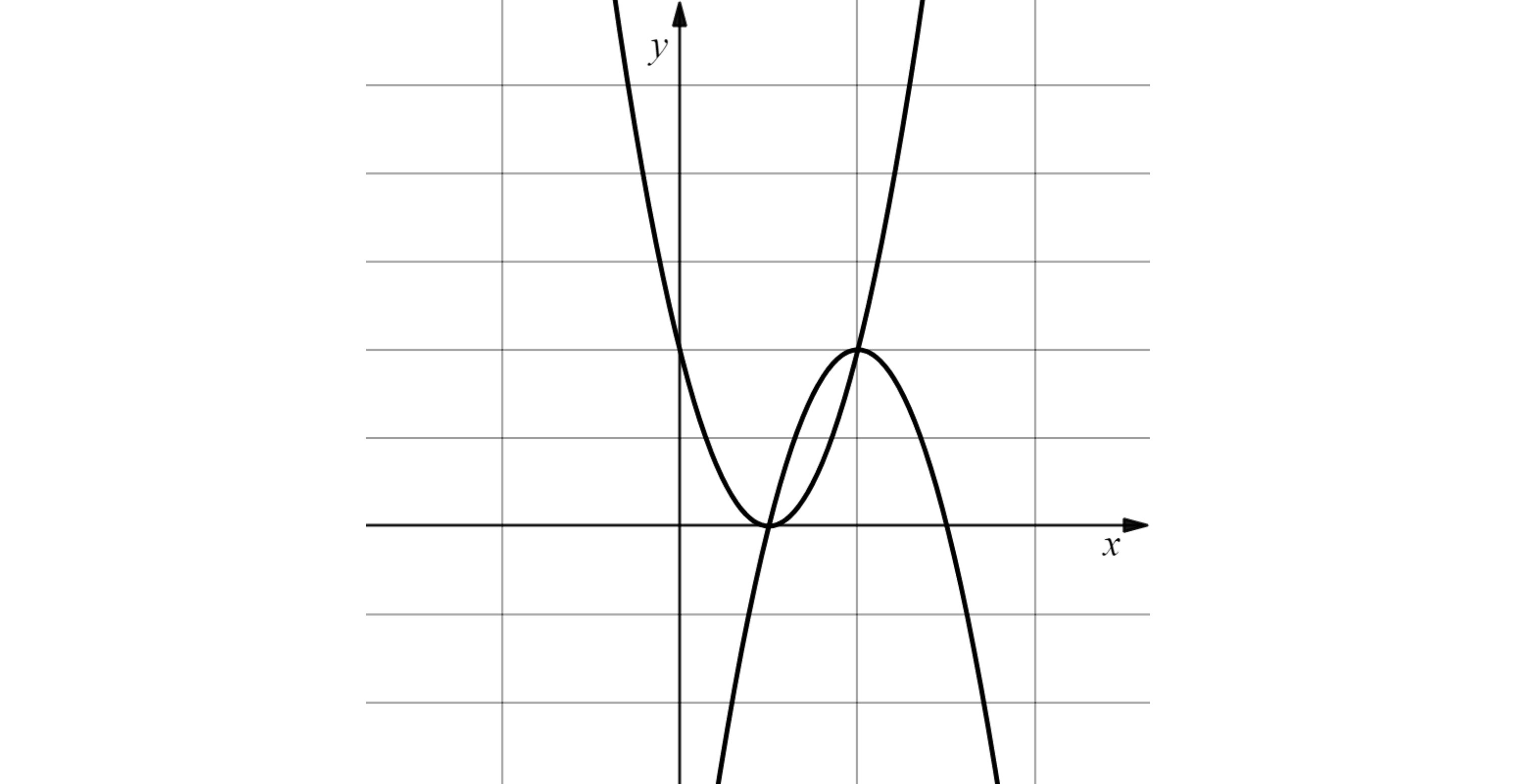
Two intersecting quadratic curves, one a negative quadratic, the other a positive quadratic. They intersect in two places.

Answer:

Find the points where the two curves intersect, by setting their equations equal to one another and solving

$\begin{array}{rcl} 2 x^{2} - 4 x + 2 & = & - 2 x^{2} + 8 x - 6 \\ 4 x^{2} - 12 x + 8 & = & 0 \\ x^{2} - 3 x + 2 & = & 0 \\ (x - 2) (x - 1) & = & 0 \end{array}$

$x = 2$ or $x = 1$

Between the intersections, the n-shaped graph (the negative quadratic) is above the u-shaped graph (the positive quadratic) so the area integral will be of the following form

$\int_{1}^{2} ((- 2 x^{2} + 8 x - 6) - (2 x^{2} - 4 x + 2)) d x$

Simplify and then find the value of the definite integral

$\begin{array}{rcl} \int_{1}^{2} (- 4 x^{2} + 12 x - 8) d x & = & {[- \frac{4}{3} x^{3} + 6 x^{2} - 8 x]}_{1}^{2} \\ = & (- \frac{4}{3} {(2)}^{3} + 6 {(2)}^{2} - 8 (2)) - (- \frac{4}{3} {(1)}^{3} + 6 {(1)}^{2} - 8 (1)) \\ = & (- \frac{8}{3}) - (- \frac{10}{3}) \\ = & \frac{2}{3} \end{array}$

$\frac{2}{3}$ units squared

Area between two curves in terms of y

How do I find the area between two curves when the functions are in terms of y?

The same concepts apply as when the functions are in terms of $x$
- but the process is followed relative to the $y$ -axis instead of the $x$ -axis
Consider the diagram below where
- The area between two curves, $x = f (y)$ and $x = g (y)$ is being found
  - bounded by the lines $y = a$ and $y = b$
- This region is labeled $R$

Graph showing a shaded region R between curves x=f(y) and x=g(y) from y=a to y=b, with an integral formula for R: ∫[a to b] (f(y) - g(y)) dy. — **Example of the area between two curves using horizontal lines**

The region $R$ is the difference between the two areas found by:
- Integrating $x = f (y)$ between $y = a$ and $y = b$
- Integrating $x = g (y)$ between $y = a$ and $y = b$
As $f (y) \geq g (y)$ for all of this interval, this area can be calculated as
- $\int_{a}^{b} f (y) d y - \int_{a}^{b} g (y) d y$
- I.e. $g (y)$ is closer to the $y$ -axis than $f (y)$ is on this interval
This is equivalent to
- $\int_{a}^{b} (f (y) - g (y)) d y$
It is essential to have the function that is further away from the $y$ -axis, be first inside the integral
- If the curves overlap and form multiple regions, see the method outlined in the 'Multiple Areas' study guide
In these scenarios we are integrating an equation for $x$ in terms of $y$
- If you are given an equation for $y$ in terms of $x$
  - you need to rearrange the equation for $x$ in terms of $y$

What if I am not told the limits?

If you are not told the limits, it is likely you are finding the area enclosed by the two curves, $f (y)$ and $g (y)$ , which intersect each other
Find the $y$ -values of the points of intersection of the two curves by solving $f (y) = g (y)$
- These will be the limits for the integral

Worked Example

The graph below shows two curves with the following equations

$y = \frac{1}{8} e^{x}$ and $y = 2 e^{- x}$

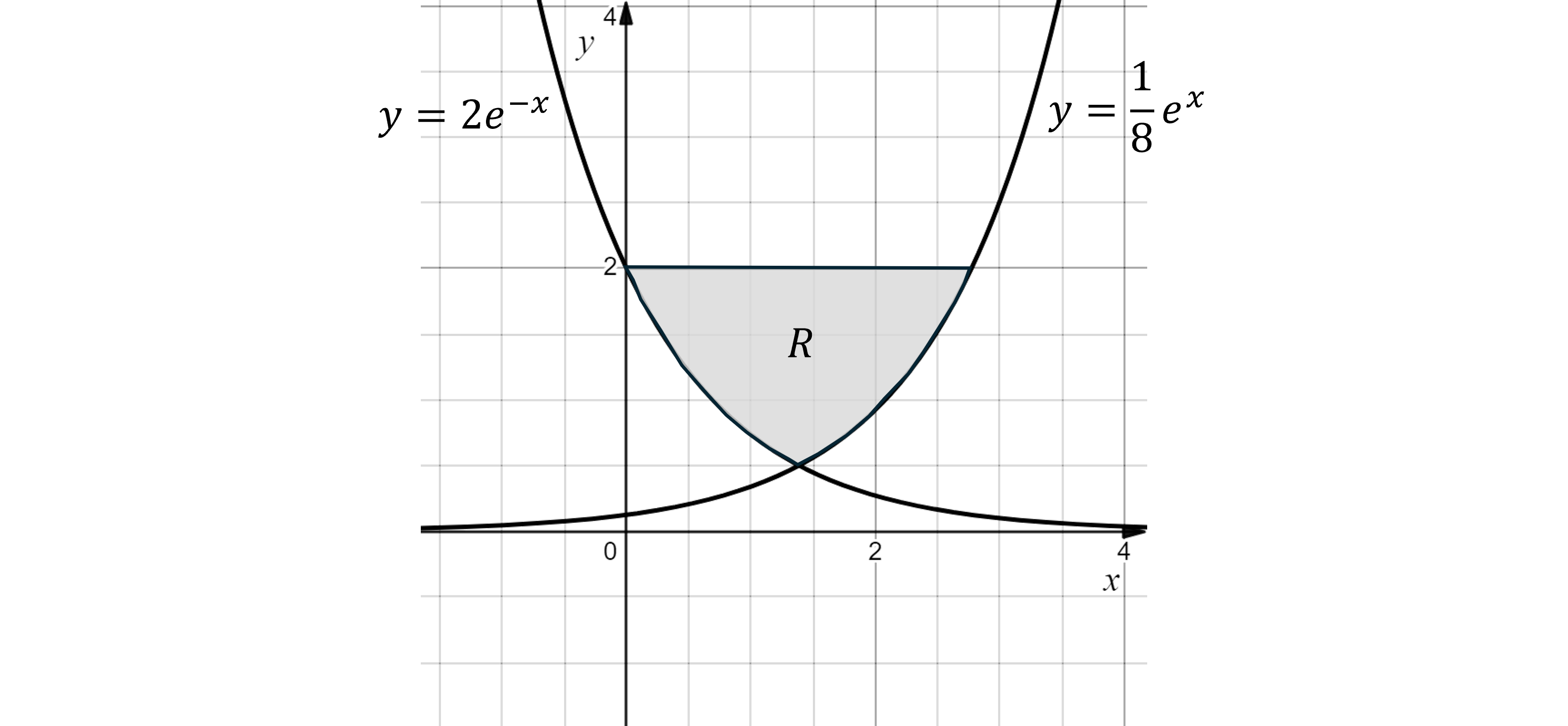
Graph of the functions y = 2e^(-x) and y = (1/8)e^(x) showing the area R bounded by the curves between x = 0 and x = 2, labeled and shaded in gray.

The region $R$ is bounded by the line $y = 2$ and the two curves. Find the area of region $R$ .

Answer:

Start by working out the integral limits

The upper limit is $y = 2$ and the lower limit will be the $y$ value of the point of intersection of the two curves

As we are working in terms of $y$ , rewrite each equation as $x$ in terms of $y$

For $y = \frac{1}{8} e^{x}$

$\begin{array}{rcl} y & = & \frac{1}{8} e^{x} \\ 8 y & = & e^{x} \\ \ln (8 y) & = & x \end{array}$

For $y = 2 e^{- x}$

$\begin{array}{rcl} y & = & 2 e^{- x} \\ \frac{y}{2} & = & e^{- x} \\ \frac{y}{2} & = & \frac{1}{e^{x}} \\ \frac{2}{y} & = & e^{x} \\ \ln (\frac{2}{y}) & = & x \end{array}$

Find the $y$ -value of the point of intersection by setting these equations equal to each other; this will be the lower limit for the integral

You could also use your calculator to find this

$\begin{array}{rcl} \ln (8 y) & = & \ln (\frac{2}{y}) \\ 8 y & = & \frac{2}{y} \\ 8 y^{2} & = & 2 \\ y^{2} & = & \frac{1}{4} \\ y & = & \pm \frac{1}{2} \end{array}$

$y$ must be positive as neither graph has any negative $y$ values

$y = \frac{1}{2}$

Use an integral of the form $\int_{a}^{b} (f (y) - g (y)) d y$

The curve with equation $y = \frac{1}{8} e^{x}$ (or $\ln (8 y) = x$ ) is furthest away from the $y$ -axis, so will come first in the integral

$\int_{\frac{1}{2}}^{2} (\ln (8 y)) - (\ln (\frac{2}{y})) d y$

You could use your calculator at this point to evaluate the integral, or you can simplify first using laws of logarithms

$\begin{array}{rcl} \ln (8 y) - \ln (\frac{2}{y}) & = & \ln (\frac{8 y}{(\frac{2}{y})}) \\ = & \ln (4 y^{2}) \\ = & \ln {(2 y)}^{2} \\ = & 2 \ln (2 y) \end{array}$

Use your calculator to evaluate the integral

$\int_{\frac{1}{2}}^{2} 2 \ln (2 y) d y = 2.54517744 . . .$

Round to 3 decimal places

2.545 units squared

Examiner Tips and Tricks

Note that the area in the example above can also be found by using areas between the curves and the $x$ -axis, and subtracting them from the rectangular area underneath the line forming the upper boundary of region $R$

$\begin{array}{rcl} Area of region R & = & (2 \times \ln 16) - \int_{0}^{\ln 4} 2 e^{- x} d x - \int_{\ln 4}^{\ln 16} \frac{1}{8} e^{x} d x \\ = & 2 \ln 16 - 3 \\ = & 2.54517744 . . . \end{array}$

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

Beth
IGCSE Student

This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

Fathima
A Level Student

Incredible! SO worth my money, the revision notes have everything I need to know and are so easy to understand. I actually enjoy revising! It makes me feel a lot more confident for my GCSEs in a few months.

Kate
GCSE Student

Absolutely brilliant, both my girls used it for A levels and GCSE. It's saves on paper copies, also beneficial exam questions ranked from easy to hard. It's removed a lot of stress from the exams.

Sameera
Parent

Just to say that your resources are the best I have seen and I have been teaching chemistry at different levels for about 40 years

Mark
Chemistry Teacher

Excellent

Area Between Two Curves (College Board AP® Calculus BC): Revision Note

Area between two curves in terms of x

How do I find the area between two curves?

What if I am not told the limits of integration?

Examiner Tips and Tricks

Worked Example

Area between two curves in terms of y

How do I find the area between two curves when the functions are in terms of y?

What if I am not told the limits?

Worked Example

Examiner Tips and Tricks

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Jamie Wood

Reviewer: Dan Finlay