AP®MathsCollege BoardCalculus BCStudy GuidesUnit 5: Analytical Applications of DifferentiationGraphs of Functions & Their DerivativesIncreasing & Decreasing Functions

Increasing & Decreasing Functions (College Board AP® Calculus BC) : Study Guide

Jamie Wood

Written by: Jamie Wood

Reviewed by: Dan Finlay

Updated on

College Board Calculus BCCollege Board Calculus AB

Increasing & decreasing functions

How do I find where a function is increasing and decreasing?

  • The first derivative of a function, f apostrophe open parentheses x close parentheses, describes the rate of change of f open parentheses x close parentheses

    • If the rate of change is positive, the function is increasing

    • If the rate of change is negative, the function is decreasing

  • This means you can determine if a function is increasing or decreasing at a point

    • If f apostrophe open parentheses a close parentheses greater or equal than 0 then f is increasing at x equals a

    • If f apostrophe open parentheses a close parentheses less or equal than 0 then f is decreasing at x equals a

    • If f apostrophe open parentheses a close parentheses equals 0 then there is a critical point at x equals a

  • You can also find an interval where a function is increasing or decreasing

    • To find where the function is increasing,

      • Solve the inequality f apostrophe open parentheses x close parentheses greater or equal than 0

    • To find where the function is decreasing,

      • Solve the inequality f apostrophe open parentheses x close parentheses less or equal than 0

Examiner Tips and Tricks

The definitions for where a function is increasing or decreasing include the endpoints, however the scoring guidelines for exam questions often allow the point to still be awarded if the endpoints are not included.

I.e. " f open parentheses x close parentheses is increasing for 1 less or equal than x less or equal than 5 " would receive the same marks as " f open parentheses x close parentheses is increasing for 1 less than x less than 5 "

  • Sketching a graph of both f open parentheses x close parentheses and f apostrophe open parentheses x close parentheses can help to identify where a function will be increasing or decreasing

    • On the graph of f open parentheses x close parentheses,

      • An upward slope from left to right is where the function is increasing

      • A downward slope from left to right is where the function is decreasing

    • On the graph of f apostrophe open parentheses x close parentheses,

      • The portion of the graph above the x-axis is where the function is increasing

      • The portion of the graph below the x-axis is where the function is decreasing

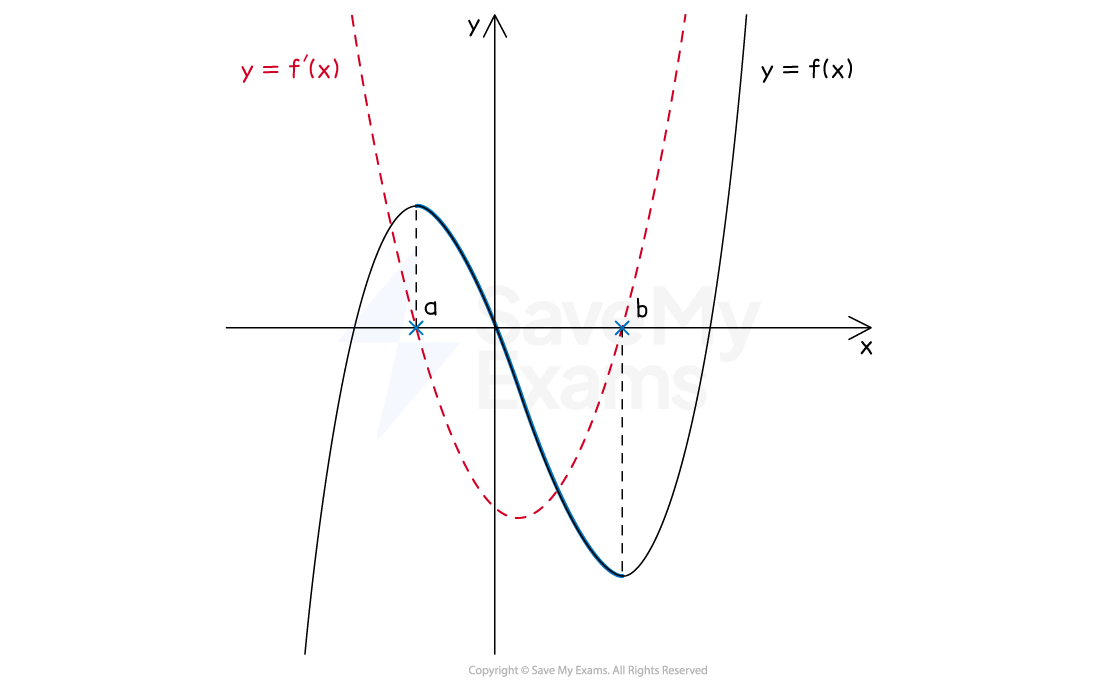
  • The diagram below shows a cubic and its derivative, a quadratic, plotted on the same graph

    • Between the critical points at a and b, the cubic is decreasing

    • Therefore the graph of the derivative is below the x-axis between a and b

Graph showing a black curve y=f(x), a red dashed curve y=f'(x). Points a and b are marked on the x-axis where f(x) changes from increasing to decreasing and vice versa
Graph of a cubic, and its derivative; a quadratic.

Worked Example

Find the interval(s) on which the graph of f open parentheses x close parentheses equals 1 fourth x to the power of 4 plus 1 third x cubed minus 3 x squared plus 4 is decreasing.

Answer:

The function is decreasing where f apostrophe open parentheses x close parentheses less or equal than 0

Find f apostrophe open parentheses x close parentheses

f apostrophe open parentheses x close parentheses equals x cubed plus x squared minus 6 x

Solve the inequality f apostrophe open parentheses x close parentheses less or equal than 0

table row cell x cubed plus x squared minus 6 x end cell less or equal than 0 row cell x open parentheses x squared plus x minus 6 close parentheses end cell less or equal than 0 row cell x open parentheses x plus 3 close parentheses open parentheses x minus 2 close parentheses end cell less or equal than 0 end table

The easiest way to solve a cubic inequality is to graph it, you could use your calculator to help you

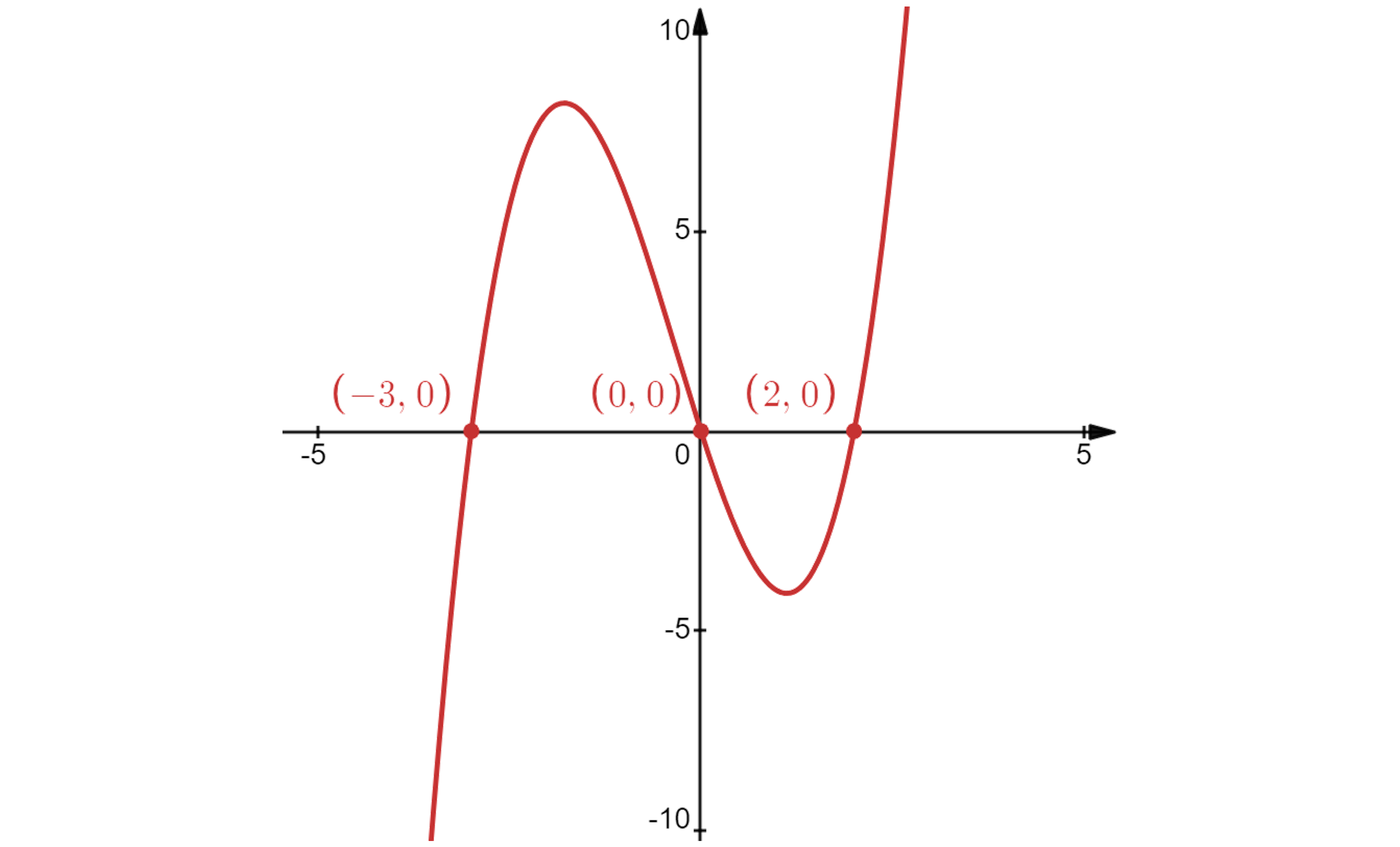
Graph of a cubic function crossing the x-axis at (-3, 0), (0, 0), and (2, 0), and the y-axis at (0, 0), with labeled coordinates.

Use the graph to identify where table row cell x open parentheses x plus 3 close parentheses open parentheses x minus 2 close parentheses end cell less or equal than 0 end table (the parts underneath the x-axis)

x less or equal than negative 3 and 0 less or equal than x less or equal than 2

So these are the regions where f apostrophe open parentheses x close parentheses less or equal than 0, therefore these are the regions where the graph of f open parentheses x close parentheses is decreasing

The question asks for intervals, rather than values of x

Decreasing on the intervals (∞, -3] and [0, 2]

👀 You've read 1 of your 5 free study guides this week
An illustration of students holding their exam resultsUnlock more study guides. It's free!

By signing up you agree to our Terms and Privacy Policy.

Already have an account? Log in

Test yourself

Did this page help you?

Previous:Critical PointsNext:First Derivative Test for Local Extrema
Author
Reviewer
Jamie Wood

Author: Jamie Wood

Expertise: Maths Content Creator

Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

Dan Finlay

Reviewer: Dan Finlay

Expertise: Maths Lead

Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

Download notes on Increasing & Decreasing Functions