AP®MathsCollege BoardCalculus ABStudy GuidesUnit 1: Limits & ContinuityLimitsSqueeze Theorem & Trigonometric Limits

Squeeze Theorem & Trigonometric Limits (College Board AP® Calculus AB)

Study Guide

Test yourself
Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Squeeze theorem

What is the squeeze theorem?

  • The squeeze theorem lets you determine limits for a function that is bounded above and below by two other functions

    • If the two bounding functions have the same limit for some x-value,

      • then the bounded function must also have the same limit at that x-value

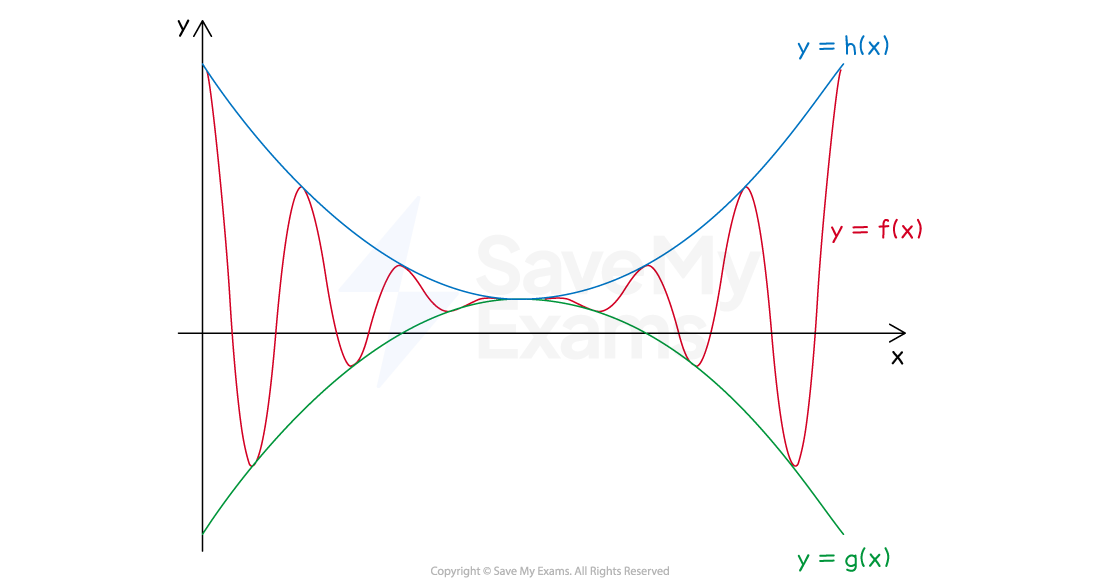
A graph illustrating the squeeze theorem, with the graph of f(x) 'squeezed' between the graphs of g(x) and h(x)

The squeeze theorem

  • Let f, g and h be functions defined on an open interval including a such that

    • g open parentheses x close parentheses less or equal than f open parentheses x close parentheses less or equal than h open parentheses x close parentheses for all x in the interval (except possibly a), and

    • limit as x rightwards arrow a of g open parentheses x close parentheses equals limit as x rightwards arrow a of h open parentheses x close parentheses equals L

  • Then limit as x rightwards arrow a of f open parentheses x close parentheses equals L

Worked Example

Let f and g be the functions defined by f open parentheses x close parentheses equals x squared minus 6 x plus 13 and g open parentheses x close parentheses equals 6 x minus x squared minus 5. It is known that g open parentheses x close parentheses less or equal than f open parentheses x close parentheses for 0 less than x less than 6.

Let h be a function such that g open parentheses x close parentheses less or equal than h open parentheses x close parentheses less or equal than f open parentheses x close parentheses for 0 less than x less than 6.

Find limit as x rightwards arrow 3 of h open parentheses x close parentheses, being sure to justify your answer.

Answer:

First find the limits for f and g

They are continuous in an open interval containing 3, so you can use substitution

limit as x rightwards arrow 3 of f open parentheses x close parentheses equals open parentheses 3 close parentheses squared minus 6 open parentheses 3 close parentheses plus 13 equals 4 limit as x rightwards arrow 3 of g open parentheses x close parentheses equals 6 open parentheses 3 close parentheses minus open parentheses 3 close parentheses squared minus 5 equals 4

Those are equal, so along with all the other given info this means you can use the squeeze theorem

Be sure to justify your answer by mentioning the squeeze theorem

By the squeeze theorem, limit as x rightwards arrow 3 of h open parentheses x close parentheses equals 4.

Trigonometric limits

What trigonometric limit theorems should I know?

  • You should know and be able to use the following two trigonometric limit theorems:

    • limit as x rightwards arrow 0 of fraction numerator sin x over denominator x end fraction equals 1

    • limit as x rightwards arrow 0 of fraction numerator cos x minus 1 over denominator x end fraction equals 0

  • These can be combined with properties of limits and/or algebraic manipulation to find other limits

    • Don't forget the trigonometric identity sin squared x plus cos squared x identical to 1

      • Which can be rearranged to give cos squared x identical to 1 minus sin squared x or sin squared x identical to 1 minus cos squared x

Examiner Tips and Tricks

You can use your graphing calculator to check any limit results that you work out analytically.

Worked Example

Find each of the following limits:

(a) limit as x rightwards arrow 0 of open parentheses fraction numerator 1 minus cos 3 x over denominator x end fraction close parentheses

Answer:

Substitution would give 0 over 0, so instead start with algebraic manipulation

fraction numerator 1 minus cos 3 x over denominator x end fraction equals fraction numerator 1 minus cos 3 x over denominator x end fraction times 3 over 3 equals fraction numerator 3 open parentheses 1 minus cos 3 x close parentheses over denominator 3 x end fraction

Now use properties of limits along with trigonometric limit theorems

We can make use of the result limit as x rightwards arrow 0 of fraction numerator cos x minus 1 over denominator x end fraction equals 0

table row cell limit as x rightwards arrow 0 of fraction numerator 3 open parentheses 1 minus cos 3 x close parentheses over denominator 3 x end fraction end cell equals cell negative 3 times limit as x rightwards arrow 0 of fraction numerator cos 3 x minus 1 over denominator 3 x end fraction end cell row blank equals cell negative 3 times 0 end cell end table

limit as x rightwards arrow 0 of open parentheses fraction numerator 1 minus cos 3 x over denominator x end fraction close parentheses equals 0

(b) limit as x rightwards arrow 0 of open parentheses fraction numerator sin 7 x over denominator sin 4 x end fraction close parentheses

Answer:

Substitution would give 0 over 0, so instead start with algebraic manipulation

table row cell fraction numerator sin 7 x over denominator sin 4 x end fraction end cell equals cell fraction numerator sin 7 x over denominator sin 4 x end fraction times fraction numerator open parentheses 1 over x close parentheses over denominator open parentheses 1 over x close parentheses end fraction times fraction numerator open parentheses 7 over 7 close parentheses over denominator open parentheses 4 over 4 close parentheses end fraction equals fraction numerator open parentheses fraction numerator 7 sin 7 x over denominator 7 x end fraction close parentheses over denominator open parentheses fraction numerator 4 sin 4 x over denominator 4 x end fraction close parentheses end fraction end cell end table

Now use properties of limits along with trigonometric limit theorems

We can make use of the result limit as x rightwards arrow 0 of fraction numerator sin x over denominator x end fraction equals 1

table row cell limit as x rightwards arrow 0 of open square brackets fraction numerator open parentheses fraction numerator 7 sin 7 x over denominator 7 x end fraction close parentheses over denominator open parentheses fraction numerator 4 sin 4 x over denominator 4 x end fraction close parentheses end fraction close square brackets end cell equals cell 7 over 4 times limit as x rightwards arrow 0 of open square brackets fraction numerator open parentheses fraction numerator sin 7 x over denominator 7 x end fraction close parentheses over denominator open parentheses fraction numerator sin 4 x over denominator 4 x end fraction close parentheses end fraction close square brackets end cell row blank equals cell 7 over 4 times fraction numerator limit as x rightwards arrow 0 of fraction numerator sin 7 x over denominator 7 x end fraction over denominator limit as x rightwards arrow 0 of fraction numerator sin 4 x over denominator 4 x end fraction end fraction end cell row blank equals cell 7 over 4 times 1 over 1 end cell end table

limit as x rightwards arrow 0 of open parentheses fraction numerator sin 7 x over denominator sin 4 x end fraction close parentheses equals 7 over 4

(c) limit as x rightwards arrow 0 of open parentheses fraction numerator 1 minus cos x over denominator x squared end fraction close parentheses

Answer:

Substitution would give 0 over 0, so instead start with algebraic manipulation

We can make use of the identity sin squared x identical to 1 minus cos squared x

table row cell fraction numerator 1 minus cos x over denominator x squared end fraction end cell equals cell fraction numerator 1 minus cos x over denominator x squared end fraction times fraction numerator 1 plus cos x over denominator 1 plus cos x end fraction end cell row blank equals cell fraction numerator 1 minus cos squared x over denominator x squared open parentheses 1 plus cos x close parentheses end fraction end cell row blank equals cell fraction numerator sin squared x over denominator x squared open parentheses 1 plus cos x close parentheses end fraction end cell row blank equals cell fraction numerator open parentheses fraction numerator sin x over denominator x end fraction close parentheses squared over denominator 1 plus cos x end fraction end cell end table

Now use properties of limits along with trigonometric limit theorems

We can make use of the results limit as x rightwards arrow 0 of fraction numerator sin x over denominator x end fraction equals 1

table row cell limit as x rightwards arrow 0 of open square brackets fraction numerator open parentheses fraction numerator sin x over denominator x end fraction close parentheses squared over denominator 1 plus cos x end fraction close square brackets end cell equals cell fraction numerator limit as x rightwards arrow 0 of open parentheses fraction numerator sin x over denominator x end fraction close parentheses squared over denominator limit as x rightwards arrow 0 of open parentheses 1 plus cos x close parentheses end fraction end cell row blank equals cell fraction numerator open parentheses limit as x rightwards arrow 0 of open parentheses fraction numerator sin x over denominator x end fraction close parentheses close parentheses squared over denominator limit as x rightwards arrow 0 of open parentheses 1 plus cos x close parentheses end fraction end cell row blank equals cell fraction numerator 1 squared over denominator 1 plus 1 end fraction end cell end table

limit as x rightwards arrow 0 of open parentheses fraction numerator 1 minus cos x over denominator x squared end fraction close parentheses equals 1 half

Last updated:

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Evaluating Limits Numerically & GraphicallyNext:Selecting Procedures for Determining Limits
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.