Evaluating Limits Numerically & Graphically (College Board AP® Calculus AB)

Study Guide

Written by: Roger B

Reviewed by: Dan Finlay

Limits from tables

How can I estimate a limit using values in a table?

Values of a function in a table can show the behavior of a function near a point
- This can allow you to estimate the limit at that point
For example, let $f$ be the function defined by $f (x) = \frac{1 - \cos x}{x^{2}}$
- The table below shows values of the function near $x = 0$
- Note that the function is not defined at $x = 0$ , because $f (0) = \frac{0}{0}$

x	f(x)
-0.1	0.49958347
-0.01	0.49999583
-0.001	0.49999996
0	not defined
0.001	0.49999996
0.01	0.49999583
0.1	0.49958347

From the table we can see that $f (x)$ gets nearer and nearer to 0.5 as $x$ gets nearer and nearer to 0
- Therefore we can estimate that $\lim_{x \to 0} f (x)$ is equal to 0.5
- Analytical methods would need to be used to confirm that this is indeed the limit

Limits from graphs

How can I estimate a limit using a graph?

A graph can show the behavior of a function near a point
- This can allow you to estimate the limit at that point
For example, let $f$ be the function defined by $f (x) = \frac{1 - \cos x}{x^{2}}$
- The graph below shows the behavior the function near $x = 0$
- Note that the function is not defined at $x = 0$ , because $f (0) = \frac{0}{0}$

A graph of the function y=(1-cosx)/x^2 between x=-2 and x=2, showing limiting behavior as x approaches zero

From the graph we can see that $f (x)$ gets nearer and nearer to 0.5 as $x$ gets nearer and nearer to 0
- Therefore we can estimate that $\lim_{x \to 0} f (x)$ is equal to 0.5
- Analytical methods would need to be used to confirm that this is indeed the limit

Examiner Tips and Tricks

You can graph functions on your graphing calculator to check your answers when determining limits analytically.

Horizontal asymptote

What is a horizontal asymptote?

A horizontal asymptote is a horizontal line
- that the graph of a function gets closer and closer to (but never touches or intersects)
- as x becomes unbounded in the positive or negative direction
On the following diagram, the horizontal asymptote is indicated by a dashed line

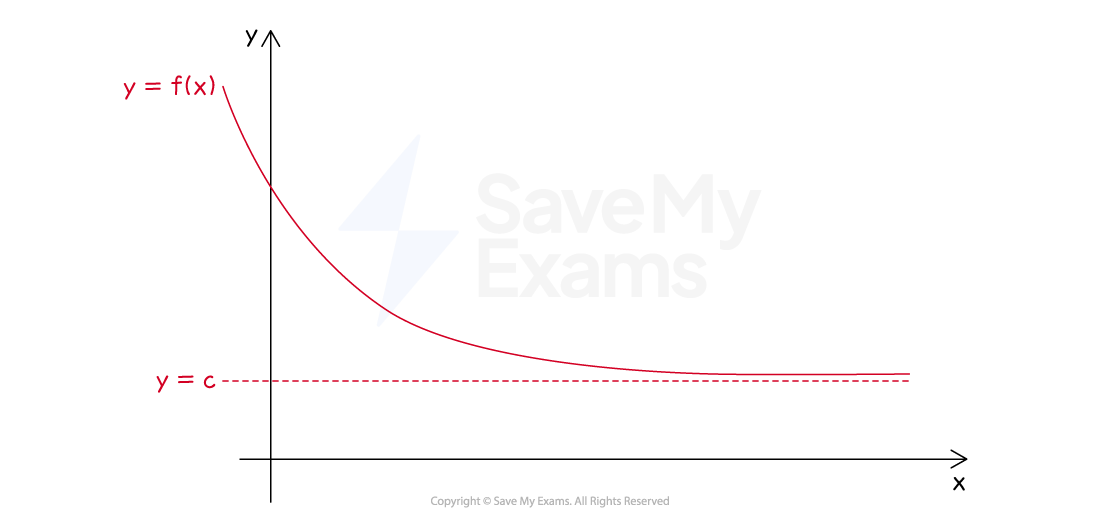
A graph of a function f with a horizontal asymptote at y=c — **An example of a function with a horizontal asymptote at y=c**

How can I identify horizontal asymptotes using limits?

A function will have a horizontal asymptote if it has a finite limit at infinity
- I.e. the line $y = c$ will be a horizontal asymptote for the graph of a function $f$ if
  - $\lim_{x \to \infty} f (x) = c$ , or
  - $\lim_{x \to - \infty} f (x) = c$
Horizontal asymptotes (if any) may therefore be determined by evaluating the limits at infinity

Examiner Tips and Tricks

By graphing a function on your graphing calculator you can:

spot any asymptotic behavior by a function at plus or minus infinity
check limits that you have determined analytically

Vertical asymptote

What is a vertical asymptote?

A vertical asymptote is a vertical line
- that the graph of a function gets closer and closer to (but never touches or intersects)
- as x gets closer and closer to the x-value of the vertical line
On the following diagram, the vertical asymptote is indicated by a dashed line

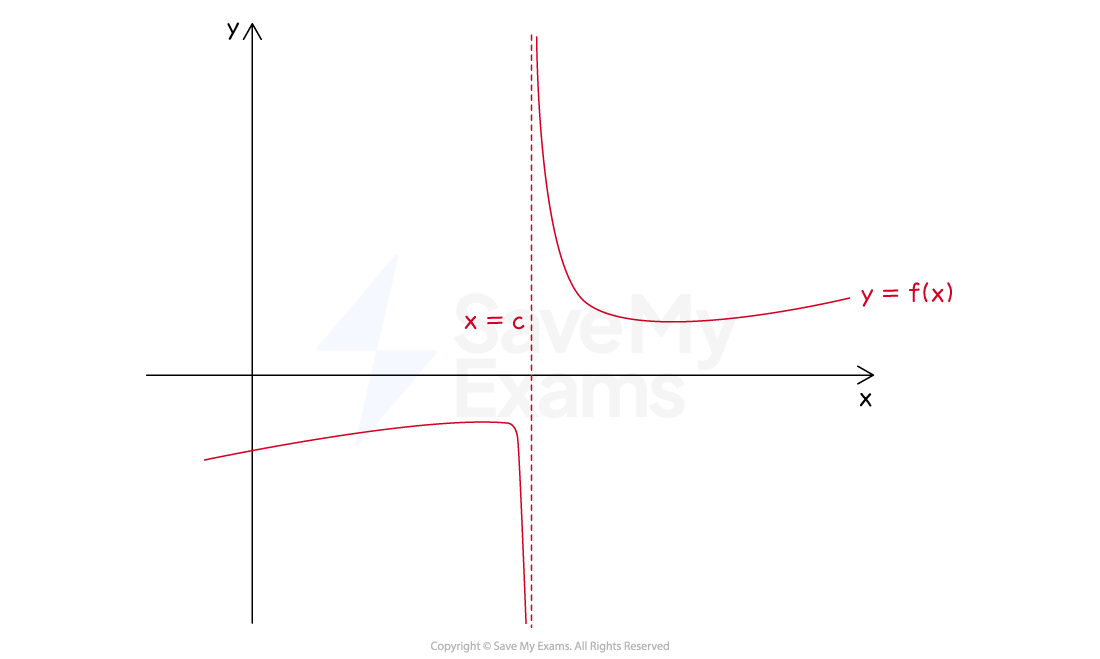
Graph of a function f with a vertical asymptote at x=c — **An example of a function with a vertical asymptote at x=c**

How can I identify vertical asymptotes using limits?

A function will have a vertical asymptote at any x-value where the function becomes unbounded
- I.e. the line $x = c$ will be a vertical asymptote for the graph of a function $f$ if
  - $\lim_{x \to c^{-}} f (x) = \pm \infty$ , or
  - $\lim_{x \to c^{+}} f (x) = \pm \infty$
Vertical asymptotes (if any) may therefore be determined by identifying points where the function becomes unbounded
- Usually this will involve a function in the form of a quotient
  - at points where the denominator becomes zero

Examiner Tips and Tricks

By graphing a function on your graphing calculator you can:

spot any asymptotic (i.e. unbounded) behavior by a function at certain values of x
check that vertical asymptotes you determine analytically are correct

Worked Example

Let $f$ be the function defined by $f (x) = \frac{3 x - 11}{x - 2}$ .

Using limits, identify the vertical and horizontal asymptotes (if any) on the graph of $f$ .

Answer:

The denominator becomes 0 when $x = 2$ , so start by considering the limits there

At 2 the numerator is equal to -5, so zero only occurs in the denominator

Just 'to the left' of 2, $3 x - 11 < 0$ and $x - 2 < 0$ so

$\lim_{x \to 2^{-}} f (x) = \infty$

Just 'to the right' of 2, $3 x - 11 < 0$ and $x - 2 > 0$ so

$\lim_{x \to 2^{+}} f (x) = - \infty$

This confirms that the graph of $f$ has a vertical asymptote at $x = 2$

To identify horizontal asymptotes, start by rearranging to make the behavior of the function more obvious

$\frac{3 x - 11}{x - 2} = \frac{3 (x - 2) - 5}{x - 2} = \frac{3 (x - 2)}{x - 2} - \frac{5}{x - 2} = 3 - \frac{5}{x - 2}$

$\frac{5}{x - 2}$ becomes closer and closer to zero as x increases in the positive or negative directions, so

$\lim_{x \to - \infty} f (x) = \lim_{x \to \infty} f (x) = 3 - 0 = 3$

This means that the graph of $f$ has a horizontal asymptote at $y = 3$

The graph of $f$ has a vertical asymptote at $x = 2$ , and a vertical asymptote at $y = 3$

Last updated: 7 August 2024

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Evaluating Limits AnalyticallyNext:Squeeze Theorem & Trigonometric Limits

Evaluating Limits Numerically & Graphically (College Board AP® Calculus AB)

Study Guide

Limits from tables

How can I estimate a limit using values in a table?

Limits from graphs

How can I estimate a limit using a graph?

Examiner Tips and Tricks

Horizontal asymptote

What is a horizontal asymptote?

How can I identify horizontal asymptotes using limits?

Examiner Tips and Tricks

Vertical asymptote

What is a vertical asymptote?

How can I identify vertical asymptotes using limits?

Examiner Tips and Tricks

Worked Example

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Roger B

Author: Dan Finlay