AP®MathsCollege BoardCalculus ABRevision NotesUnit 1: Limits & ContinuityLimitsDefinition of a Limit

Definition of a Limit (College Board AP® Calculus AB)

Revision Note

Roger B

Author

Roger B

Expertise

Maths

What are limits in mathematics?

  • When we consider a limit in mathematics we look at the tendency of a mathematical process as it approaches, but never quite reaches, an ‘end point’ of some sort

    • Most of the key ideas in calculus rely on limits for their basic definitions

    • In this course you will be usually considering the limits of functions

  • A special limit notation is used to indicate this

    • For example limit as x rightwards arrow c of invisible function application f open parentheses x close parentheses denotes ‘the limit of the function f as x goes to (or approaches) c’

      • I.e., what value (if any) f(x) gets closer and closer to as x takes on values closer and closer to c

        • If the limit exists, we write limit as x rightwards arrow c of invisible function application f open parentheses x close parentheses equals R (where R is a real number)

        • In that case the value of f(x) can be made as close as you want to R, by making x sufficiently close to (but not equal to) c

      • We are not concerned here with what value (if any) f(x) takes when x is equal to c

        • We only care about the behaviour of f(x) as x gets close to c

One-sided limit

What are one-sided limits?

  • A one-sided limit is only concerned with the value of the function as you approach a particular value of x from one side or the other

  • limit as x rightwards arrow c to the power of minus of f open parentheses x close parentheses indicates the one-sided limit from the left (or from below)

    • It is the value that f(x) approaches as x gets closer and closer to c from the x<c side

  • limit as x rightwards arrow c to the power of plus of f open parentheses x close parentheses indicates the one-sided limit from the right (or from above)

    • It is the value that f(x) approaches as x gets closer and closer to c from the x>c side

Worked Example

The figure below shows the graph of the function f defined by f open parentheses x close parentheses equals open curly brackets table row cell x plus 1 comma space space x less or equal than 2 end cell row cell 4 comma space space x greater than 2 end cell end table close.

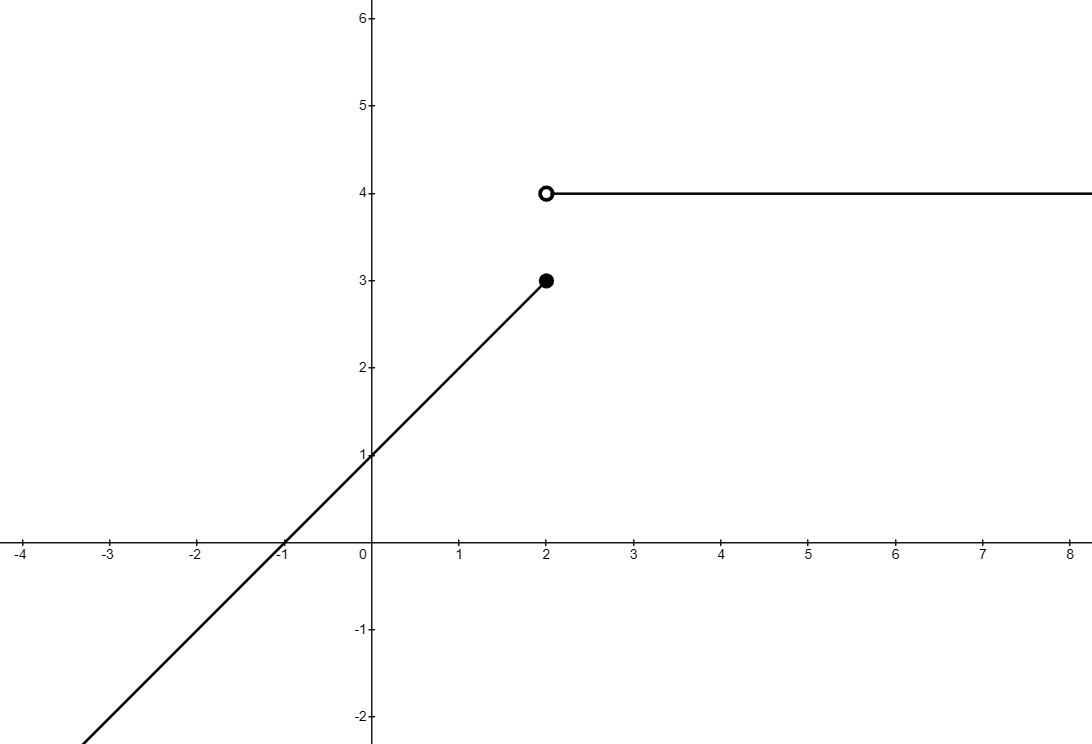
A graph of y=x+1 for x<=2, and y=4 for x>2

Find:

(a) f open parentheses 2 close parentheses

Answer:

This is simply the value of the function when x equals 2

f open parentheses 2 close parentheses equals 3

(b) limit as x rightwards arrow 2 to the power of minus of f open parentheses x close parentheses

Answer:

This is the one-sided limit from the left

From the graph, or from considering the function algebraically, we can see that the value of the function gets closer and closer to 3 as x gets close to 2 from the left

limit as x rightwards arrow 2 to the power of minus of f open parentheses x close parentheses equals 3

(c) limit as x rightwards arrow 2 to the power of plus of f open parentheses x close parentheses

Answer:

This is the one-sided limit from the right

From the graph, or from considering the function algebraically, we can see that the value of the function is always equal to 4 as x gets closer and closer to 2 from the right

Note that it doesn't matter what the value of the function is at x equals 2

limit as x rightwards arrow 2 to the power of plus of f open parentheses x close parentheses equals 4

Two-sided limit

What are two-sided limits?

  • The two-sided limit (or simply the limit) of a function f at the value x=c is denoted by limit as x rightwards arrow c of f open parentheses x close parentheses

  • To find a two-sided limit, consider the one-sided limits from the left and the right

    • If the two one-sided limits are equal, then that is the value of the two-sided limit

    • If the two one-sided limits are not equal, then the two-sided limit for that x value doesn't exist

Worked Example

The figure below shows the graph of the function f defined by f open parentheses x close parentheses equals open curly brackets table row cell x squared plus 1 comma space space x not equal to 0 end cell row cell 0 comma space space x equals 0 end cell end table close.

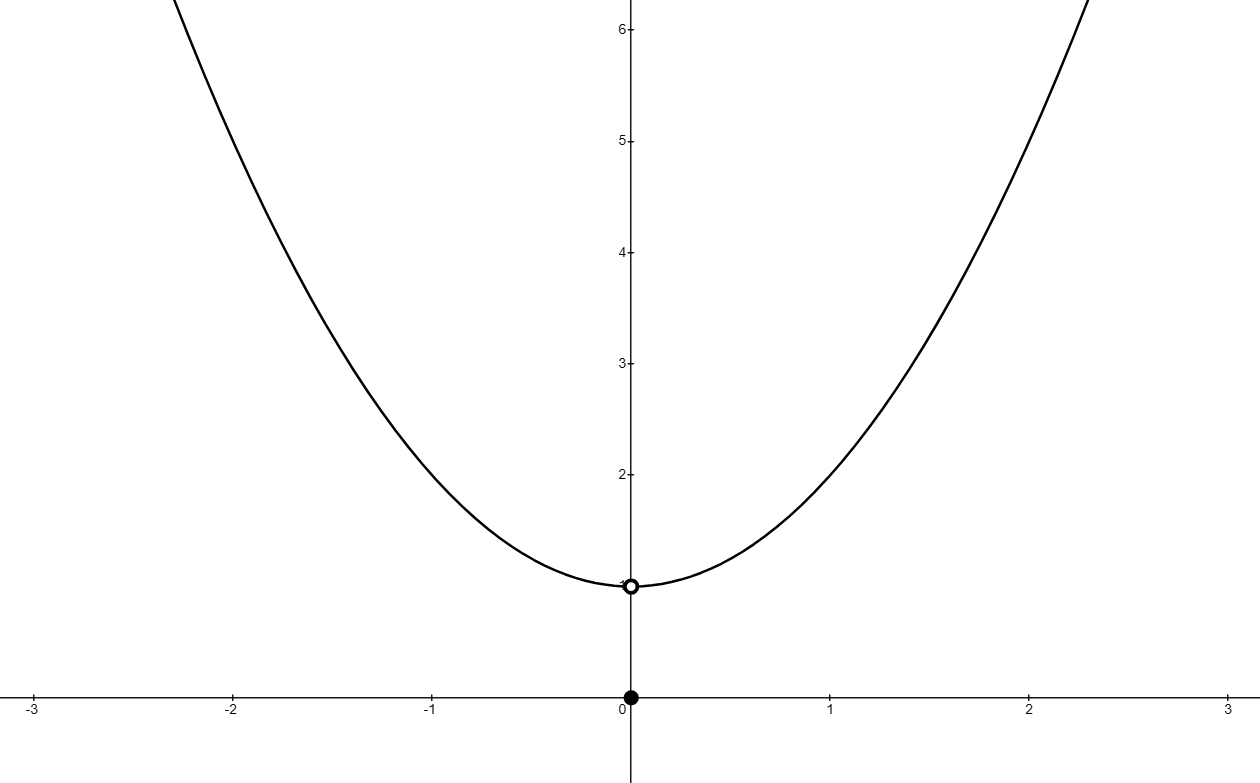
Graph of y=x^2+1 for x not equal to 0, and y=0 for x=0

Find:

(a) f open parentheses 0 close parentheses

Answer:

This is simply the value of the function when x equals 0

f open parentheses 0 close parentheses equals 0

(b) limit as x rightwards arrow 0 of f open parentheses x close parentheses

Answer:

The limit does not care what the value at x equals 0 is; it only cares what happens as x gets close to zero

From the graph, or from considering the function algebraically, we can see that the value of the function gets closer and closer to 1 as x gets close to zero

limit as x rightwards arrow 0 of f open parentheses x close parentheses equals 1

Nonexistent limits

When does the limit of a function at a point not exist?

  • For some functions, a limit might not exist for certain values of x

    • We say that the limit is nonexistent for such cases

  • There are three common ways that a limit may not exist at a point:

Case 1: The function is unbounded near the point in question

  • E.g., consider the function f defined by f open parentheses x close parentheses equals 1 over x

    • limit as x rightwards arrow 0 of f open parentheses x close parentheses does not exist because the function becomes unbounded as x approaches 0

      • It is unbounded in the positive direction as x approaches 0 from the right

      • And in the negative direction as x approaches 0 from the left

Case 2: The function oscillates near the point in question

  • E.g., consider the function g defined by g open parentheses x close parentheses equals cos open parentheses 1 over x close parentheses

    • limit as x rightwards arrow 0 of g open parentheses x close parentheses does not exist because the function oscillates as x approaches 0

      • The function is not unbounded near zero (its values are always between -1 and 1)

      • But it oscillates rapidly between -1 and 1 and never 'settles down' to a single value

Case 3: The one-sided limits are not equal at the point in question

  • E.g., consider the function h defined by h open parentheses x close parentheses equals open curly brackets table row cell 0 comma space space x less than 0 end cell row cell 1 half comma space space x equals 0 end cell row cell 1 comma space space x greater than 0 end cell end table close

    • limit as x rightwards arrow 0 of h open parentheses x close parentheses does not exist because the limit from the left does not equal the limit from the right at 0

      • limit as x rightwards arrow 0 to the power of minus of h open parentheses x close parentheses equals 0 but limit as x rightwards arrow 0 to the power of plus of h open parentheses x close parentheses equals 1

      • It doesn't matter that h open parentheses 0 close parentheses has a well-defined value!

Worked Example

Explain why each of the following limits is nonexistent:

(a) limit as x rightwards arrow negative 1 of sin open parentheses fraction numerator 1 over denominator x squared minus 1 end fraction close parentheses

Answer:

Note that when x equals negative 1, x squared minus 1 equals 0

The function is undefined at x equals negative 1, but that isn't what makes the limit non-existent; rather it's the way the function starts to oscillate as x gets close to negative 1 colon

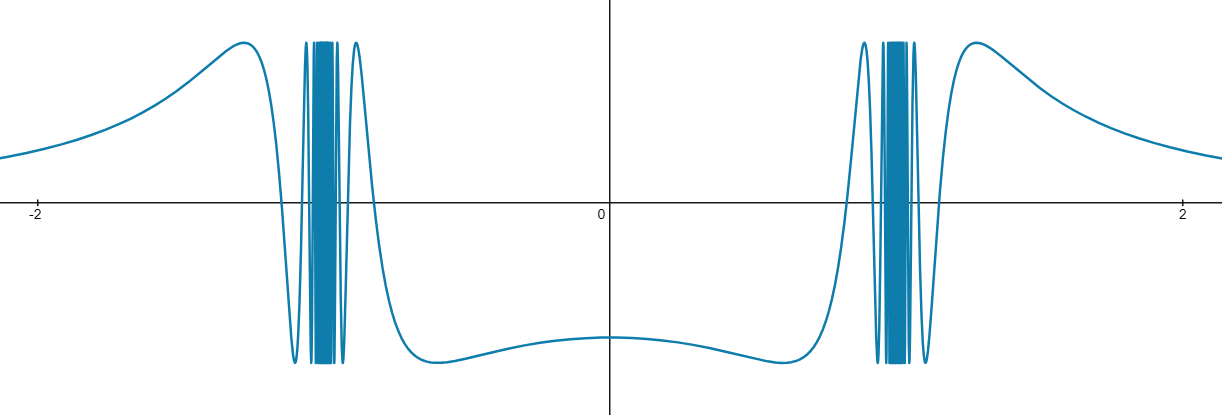
A graph of y=sin(1/(x^2-1)) from x=-2 to x=2

As x gets close to -1, x2-1 gets close to zero. Therefore the function oscillates between -1 and 1 as x approaches -1, which means the limit does not exist.

(b) limit as x rightwards arrow pi over 2 of tan x

Answer:

Remember what happens to the graph of tan x as x gets near to pi over 2:

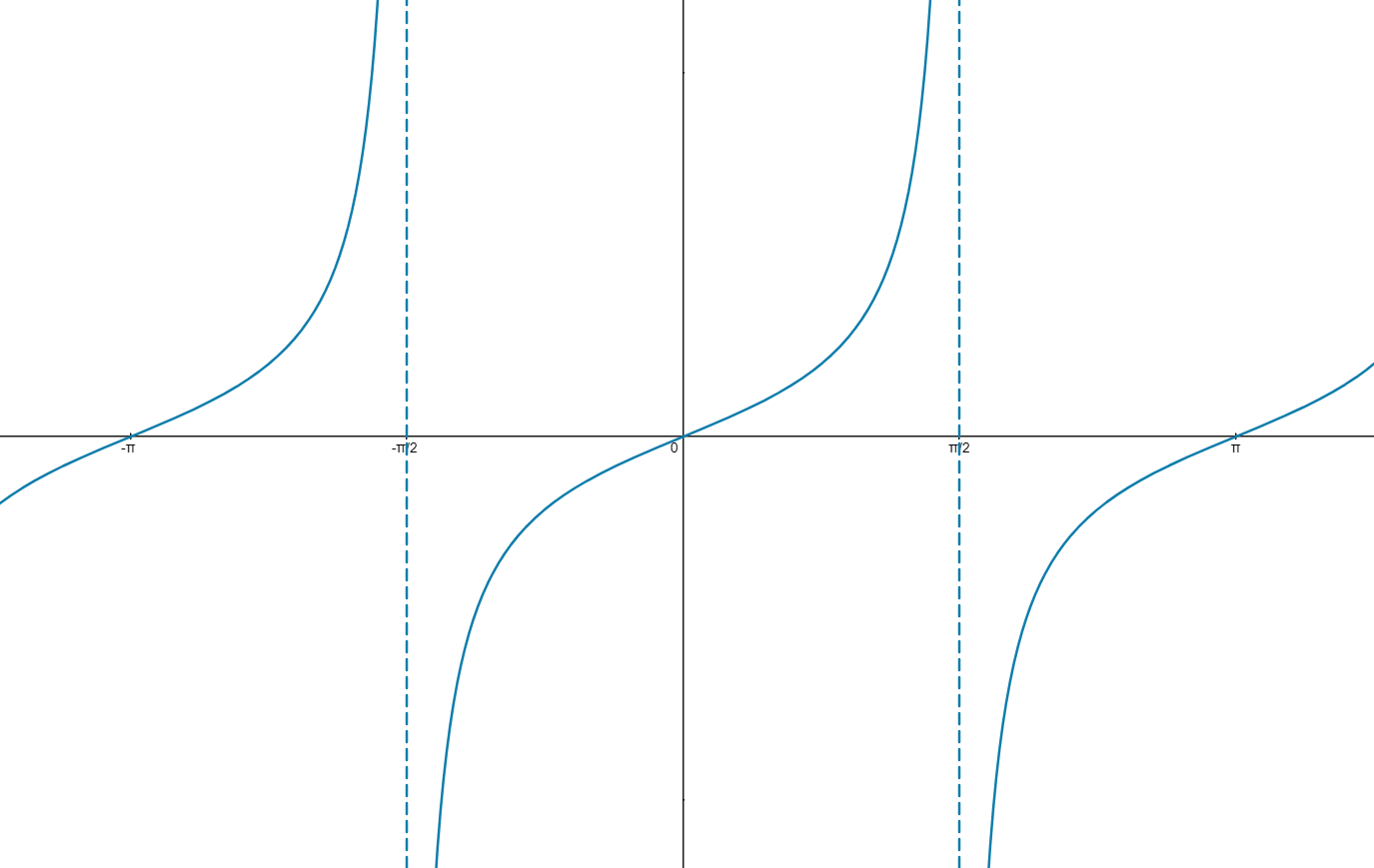
A graph of y=tanx between -π and π, showing asymptotes at -π/2 and π/2

tanx becomes unbounded as x approaches π/2 from the left and right. Therefore the limit does not exist.

(c) limit as x rightwards arrow 0 of f open parentheses x close parentheses, where f is the function defined by f open parentheses x close parentheses equals open curly brackets table row cell negative pi comma space space x less than 0 end cell row cell pi comma space space x greater or equal than 0 end cell end table close

Answer:

The graph of the function can show the problem with the limit here:

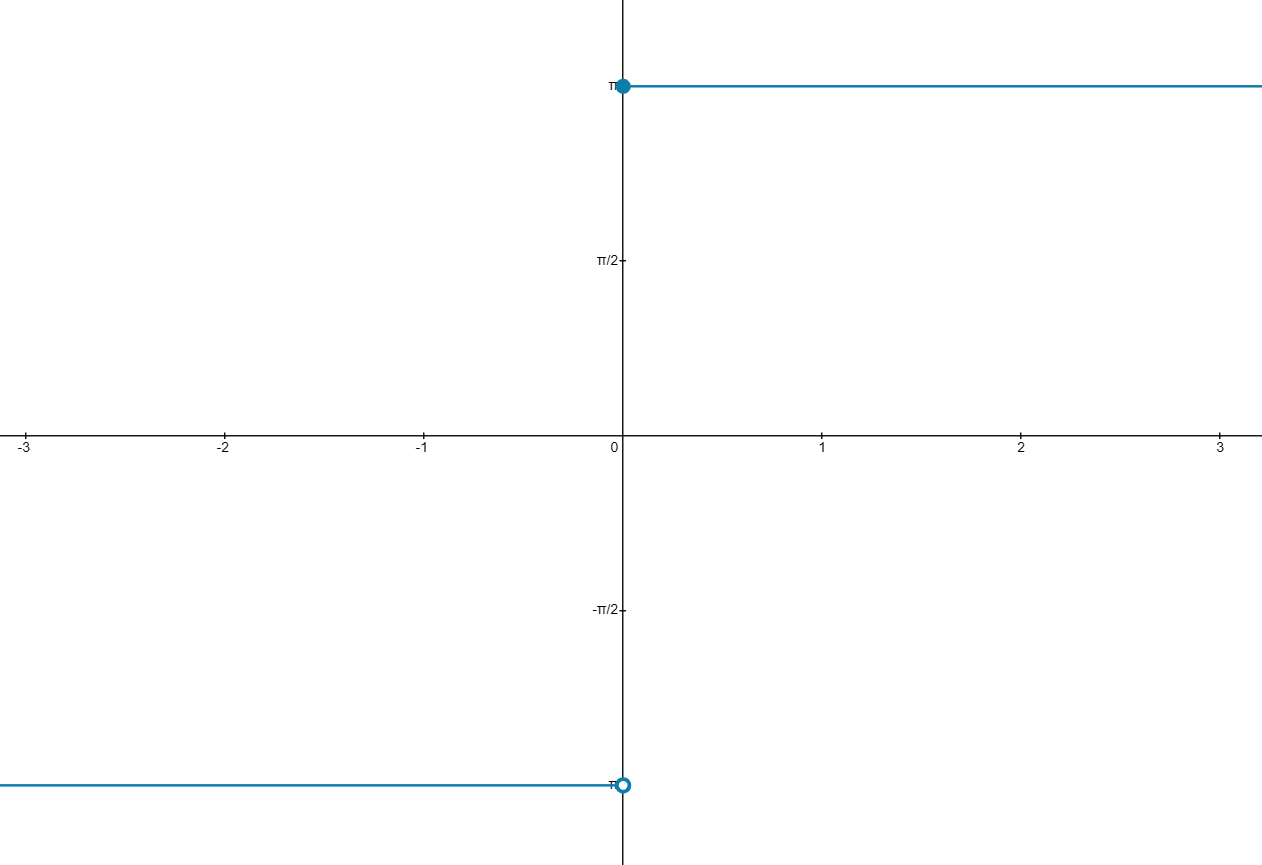
A graph of y=-π for x<0 and y=π for x>=0


limit as x rightwards arrow 0 to the power of minus of f open parentheses x close parentheses equals negative pi

limit as x rightwards arrow 0 to the power of plus of f open parentheses x close parentheses equals pi

The limits from the left and right at x=0 are not equal, therefore the limit does not exist.

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Next topic

    Did this page help you?

    Roger B

    Author: Roger B

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.