AP®MathsCollege BoardCalculus ABRevision NotesUnit 1: Limits & ContinuityContinuityNon-removable Discontinuities

Non-removable Discontinuities (College Board AP® Calculus AB)

Revision Note

Roger B

Author

Roger B

Expertise

Maths

Jump discontinuity

What is a jump discontinuity?

  • A jump continuity occurs at a point where the value of a function makes a sudden 'leap' between two values

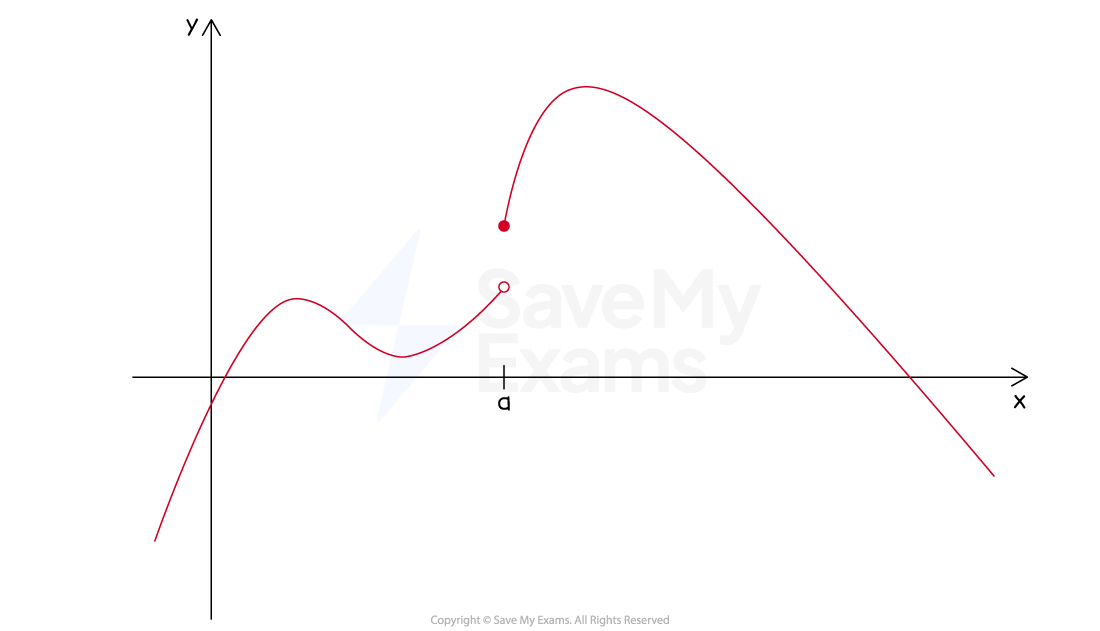
An example of the graph of a function with a jump discontinuity at x=a
Graph of a function with a jump discontinuity at x=a

  • Where there is a jump discontinuity

    • The limit from the left and the limit from the right both exist

    • But they are not equal

  • A jump discontinuity is not a removable discontinuity

  • For example, consider the function f defined by f open parentheses x close parentheses equals open curly brackets table row cell x cubed minus x squared minus 2 x comma space space x less than 1 end cell row cell 8 minus x squared minus 3 x comma space space x greater or equal than 1 end cell end table close

    • limit as x rightwards arrow 1 to the power of minus of f open parentheses x close parentheses equals negative 2

    • limit as x rightwards arrow 1 to the power of plus of f open parentheses x close parentheses equals 4

    • So f has a jump discontinuity at x equals 1

Essential discontinuity

  • A function has an essential (or infinite) discontinuity at a point where

    • the limit from the left or the limit from the right (or both)

      • do not exist

      • or are infinite

  • A common example is where the graph of a function has a vertical asymptote

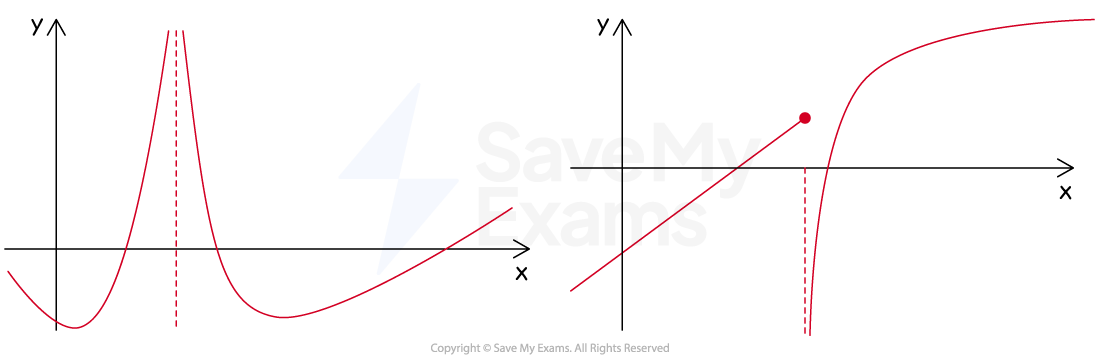
Two examples of graphs of functions with essential discontinuities
Graphs of functions with essential discontinuities

  • An essential discontinuity is not a removable discontinuity

  • For example, consider the function f defined by f open parentheses x close parentheses equals open curly brackets table row cell x minus 3 comma space space x less or equal than 5 end cell row cell 4 minus fraction numerator 1 over denominator x minus 5 end fraction comma space space x greater than 5 end cell end table close

    • limit as x rightwards arrow 5 to the power of minus of f open parentheses x close parentheses equals 2 (and f open parentheses 5 close parentheses equals 2 as well)

    • But limit as x rightwards arrow 5 to the power of plus of f open parentheses x close parentheses equals negative infinity

    • Because the right-hand limit is infinite, f has an essential discontinuity at x equals 5

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Next topic

    Did this page help you?

    Roger B

    Author: Roger B

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.