Study GuidesExam QuestionsPast Papers
AP®MathsCollege BoardCalculus ABStudy GuidesUnit 6: Integration & Accumulation of ChangeRiemann Sums & Definite IntegralsTrapezoidal Sums

Trapezoidal Sums (College Board AP® Calculus AB)

Study Guide

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Trapezoidal sums

What is a trapezoidal sum?

  • A trapezoidal sum is another method for approximating the exact value of an accumulation of change

    • Equivalently, it is a method for approximating the exact value of a definite integral

    • Or the exact area between a curve and the x-axis

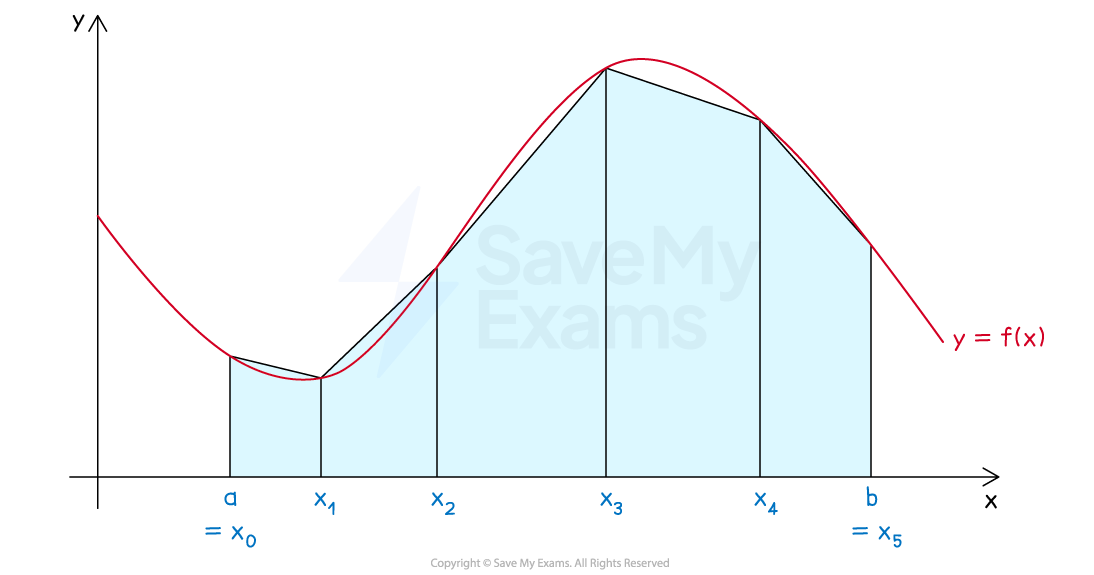
  • The approximation is made by adding up the areas of a number of trapezoids

How do I calculate a trapezoidal sum?

  • To calculate the trapezoidal sum of a function f between x equals a and x equals b (where a less than b):

    • Divide the interval into n subintervals by choosing values x subscript 0 comma space x subscript 1 comma space... comma space x subscript n such that a equals x subscript 0 less than x subscript 1 less than midline horizontal ellipsis less than x subscript n equals b

      • The intervals do not need to be the same size

    • Let this define n trapezoids

      • The ith trapezoid has a width of open parentheses x subscript i minus x subscript i minus 1 end subscript close parentheses

        • This is the distance from the left-hand side of the trapezoid to the right-hand side

      • The parallel sides of the ith trapezoid have heights of f open parentheses x subscript i minus 1 end subscript close parentheses and f open parentheses x subscript i close parentheses

        • These are the values of the function at the left-hand side and right-hand side of the trapezoid

      • The area of the ith trapezoid is space open parentheses x subscript i minus x subscript i minus 1 end subscript close parentheses times space fraction numerator f open parentheses x subscript i minus 1 end subscript close parentheses plus f open parentheses x subscript i close parentheses over denominator 2 end fraction

    • The trapezoidal sum is the sum of the areas of these n trapezoids

      • open parentheses x subscript 1 minus x subscript 0 close parentheses times fraction numerator f open parentheses x subscript 0 close parentheses plus f open parentheses x subscript 1 close parentheses over denominator 2 end fraction plus open parentheses x subscript 2 minus x subscript 1 close parentheses times fraction numerator f open parentheses x subscript 1 close parentheses plus f open parentheses x subscript 2 close parentheses over denominator 2 end fraction plus horizontal ellipsis plus open parentheses x subscript n minus x subscript n minus 1 end subscript close parentheses times fraction numerator f open parentheses x subscript n minus 1 end subscript close parentheses plus f open parentheses x subscript n close parentheses over denominator 2 end fraction

An example of the graph of a curve, showing the trapezoids used to calculate a trapezoidal sum
An example of a trapezoidal sum with n=5

  • In general, increasing the number of trapezoids, n, gives a more accurate approximation

  • On the exam you may just be given values of the function in a table, rather than being given the function explicitly

    • See the Worked Example

What if all the intervals in a trapezoidal sum have the same size?

  • If the intervals used for a trapezoidal sum all have the same size then the formula can be simplified slightly

  • The width of each trapezoid will be fraction numerator b minus a over denominator n end fraction

  • So the trapezoidal sum will become

    • fraction numerator b minus a over denominator n end fraction times fraction numerator f open parentheses x subscript 0 close parentheses plus f open parentheses x subscript 1 close parentheses over denominator 2 end fraction plus fraction numerator b minus a over denominator n end fraction times fraction numerator f open parentheses x subscript 1 close parentheses plus f open parentheses x subscript 2 close parentheses over denominator 2 end fraction plus horizontal ellipsis plus fraction numerator b minus a over denominator n end fraction times fraction numerator f open parentheses x subscript n minus 1 end subscript close parentheses plus f open parentheses x subscript n close parentheses over denominator 2 end fraction

  • By collecting terms and simplifying, this can be rearranged as

    • fraction numerator b minus a over denominator n end fraction times open square brackets fraction numerator f open parentheses x subscript 0 close parentheses plus f open parentheses x subscript n close parentheses over denominator 2 end fraction plus f open parentheses x subscript 1 close parentheses plus horizontal ellipsis plus f open parentheses x subscript n minus 1 end subscript close parentheses close square brackets

    • or space fraction numerator b minus a over denominator 2 n end fraction times open square brackets f open parentheses x subscript 0 close parentheses plus f open parentheses x subscript n close parentheses plus 2 open parentheses f open parentheses x subscript 1 close parentheses plus horizontal ellipsis plus f open parentheses x subscript n minus 1 end subscript close parentheses close parentheses close square brackets

  • It may be easier for you to understand how the trapezoidal sum is calculated

    • than to try and remember that formula

How can I tell if a trapezoidal sum is an underestimate or an overestimate?

  • If a function is concave up over the interval for which a trapezoidal sum is being calculated

    • then the trapezoidal sum will be an overestimate

  • If a function is concave down over the interval for which a trapezoidal sum is being calculated

    • then the trapezoidal sum will be an underestimate

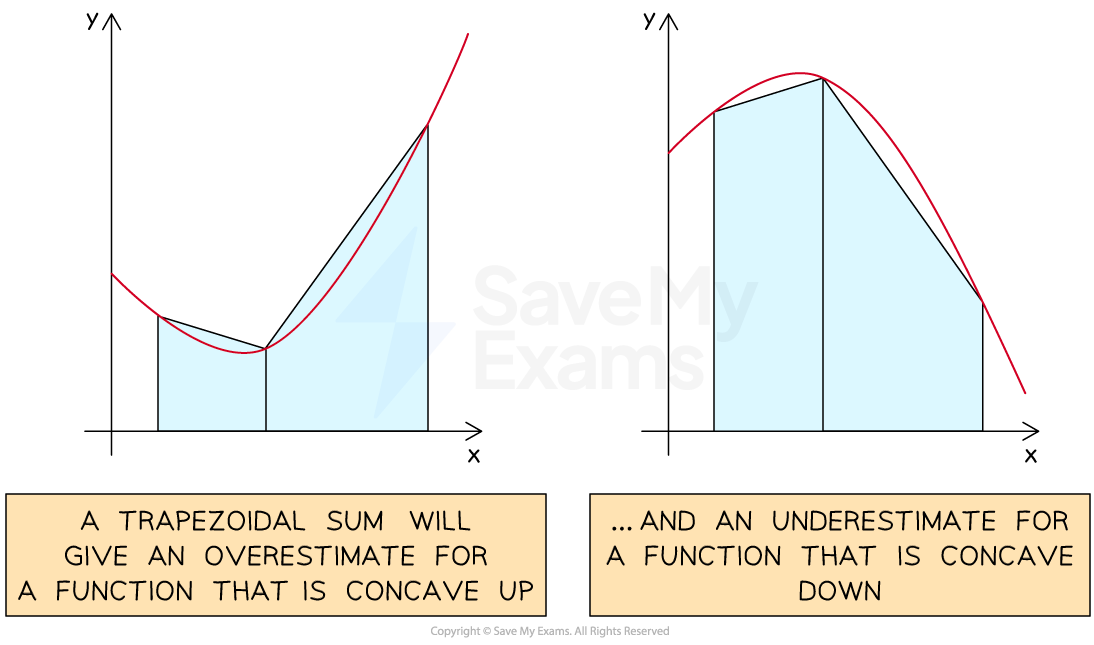
Two graphs with the trapezoids used to calculate a trapezoidal sum, showing that a trapezoidal sum will give an overestimate for a function that is concave up, and an underestimate for a function that is concave down

  • If a function has portions that are both concave up and concave down, then it is not immediately obvious whether a trapezoidal sum will be an underestimate or an overestimate

Worked Example

A social sciences researcher is using a function m to model the total mass of all the garden gnomes appearing on lawns in a particular neighborhood at time t. The function m is twice-differentiable, with m open parentheses t close parentheses measured in kilograms and t measured in days.

The table below gives selected values of m to the power of apostrophe open parentheses t close parentheses, the rate of change of the mass, over the time interval 0 less or equal than t less or equal than 12. At time t equals 0, m open parentheses 0 close parentheses equals 24.9 kilograms.

t

(days)

0

3

7

10

12

m to the power of apostrophe open parentheses t close parentheses

(kilograms per day)

2.6

4.8

12.2

0.7

-1.3

Use a trapezoidal sum with the four subintervals indicated in the table to find an estimate for the total mass of the garden gnomes at t equals 12.

Answer:

The trapezoidal sum will be based on four trapezoids

The first trapezoid will have a width of (3-0) and parallel sides of height m apostrophe open parentheses 0 close parentheses and m apostrophe open parentheses 3 close parentheses
The second trapezoid will have a width of (7-3) and parallel sides of height m apostrophe open parentheses 3 close parentheses and m apostrophe open parentheses 7 close parentheses
The third trapezoid will have a width of (10-7) and parallel sides of height m apostrophe open parentheses 7 close parentheses and m apostrophe open parentheses 10 close parentheses
The fourth trapezoid will have a width of (12-10) and parallel sides of height m apostrophe open parentheses 10 close parentheses and m apostrophe open parentheses 12 close parentheses

open parentheses 3 minus 0 close parentheses times fraction numerator 2.6 plus 4.8 over denominator 2 end fraction plus open parentheses 7 minus 3 close parentheses times fraction numerator 4.8 plus 12.2 over denominator 2 end fraction plus open parentheses 10 minus 7 close parentheses times fraction numerator 12.2 plus 0.7 over denominator 2 end fraction plus open parentheses 12 minus 10 close parentheses times fraction numerator 0.7 plus open parentheses negative 1.3 close parentheses over denominator 2 end fraction equals 63.85

This has units of kilograms, because each term is the product of a 'kg/day' quantity and a 'days' quantity

However that answer only approximates the change in mass

To find the estimate for the total final mass, add the initial mass of 24.9 kilograms

63.85 plus 24.9 equals 88.75

The total mass of garden gnomes at t equals 12 is approximately 88.75 kg

Last updated:

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Riemann SumsNext:Accumulation Functions
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.