AP®MathsCollege BoardCalculus ABStudy GuidesUnit 6: Integration & Accumulation of ChangeRiemann Sums & Definite IntegralsProperties of Definite Integrals

Properties of Definite Integrals (College Board AP® Calculus AB)

Study Guide

Test yourself
Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Definite integrals

What is a definite integral?

  • A definite integral is written in the form

    • integral subscript a superscript b f open parentheses x close parentheses space d x

      • f open parentheses x close parentheses is the function being integrated (also known as the integrand)

      • d x indicates that the function is being integrated with respect to x

      • a and bare the integration limits

        • the function is integrated 'from a to b'

      • You'll most often see definite integrals with a less or equal than b

        • But integrals with a greater than b are also valid

  • A definite integral can be interpreted in a number of ways

    • It is a mathematical operation that outputs a number

      • based on f open parentheses x close parentheses and the values of a and b

    • If f open parentheses x close parentheses is interpreted as a rate of change function

      • then the definite integral is the accumulation of change as x goes from a to b

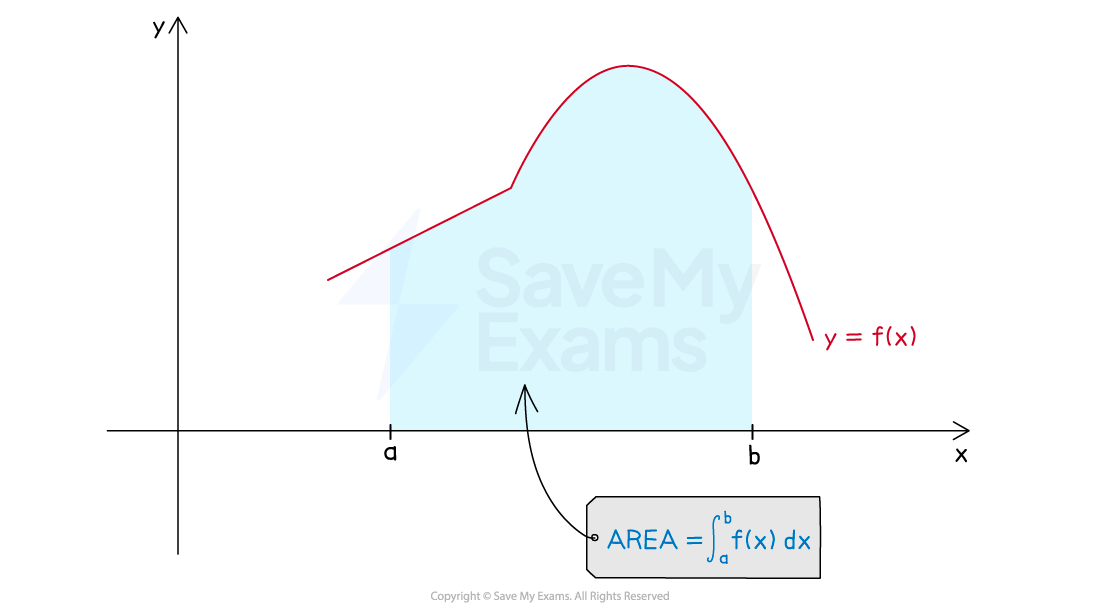
    • On the graph of y equals f open parentheses x close parentheses, where f open parentheses x close parentheses greater or equal than 0 on the interval open square brackets a comma space b close square brackets

      • the definite integral gives the area between y equals f open parentheses x close parenthesesand the x-axis, between x equals a and x equals b

A graph of a function y=f(x), showing the area under the curve between x=a and x=b as a definite integral

How is a definite integral defined as a limit of Riemann sums?

  • The value of a definite integral can be defined as a limit of Riemann sums:

    • Error converting from MathML to accessible text.

      • n is the number of subintervals used for the sum

        • This is the same as the number of rectangles

      • x subscript i superscript italic ∗ is a value of x in the ith subinterval

        • note that this is any value in the ith subinterval

      • straight capital delta x subscript i is the width of the ith subinterval

        • i.e. the width of the ith rectangle

      • limit as max space straight capital delta x subscript i rightwards arrow 0 of means the limit as the width of the largest subinterval (and hence of all subintervals) approaches zero

    • As the subintervals (and rectangles) get narrower and narrower

      • the area of the approximating rectangles gets closer and closer to the exact area under the curve

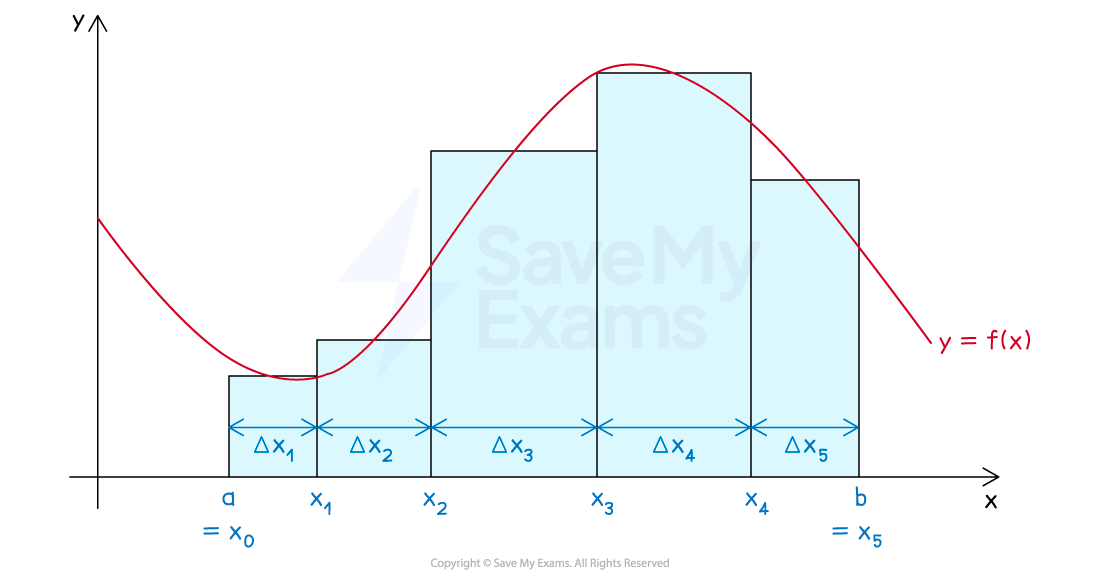
A graph of a function y=f(x) showing some of the quantities used when defining a definite integral as a limit of Riemann sums

  • Note that having the width of the largest subinterval approach zero

    • is equivalent to having the number of subintervals approach infinity

  • Therefore the Riemann sum limit for a definite integral can also be written with n as the limit index

    • Error converting from MathML to accessible text.

      • If the subintervals are assumed to be of equal width, then expressions for Error converting from MathML to accessible text. and straight capital delta x subscript i can be written in terms of a, b and n

      • See the Worked Example

Examiner Tips and Tricks

You are not expected to work out the value of a definite integral using the limit of Riemann sums!

  • See the 'Evaluating Definite Integrals' study guide for the method that is usually used

But you should be able to recognise limit and definite integral expressions that are equivalent

Worked Example

Evaluate the following limit

Error converting from MathML to accessible text.

Answer:

The trick here is recognizing this as a limit of Riemann sums

The key term is 5 over n

  • For a Riemann sum with equal subintervals and a total interval width of 5, this is the width of the ith subinterval

    • I.e.space b minus a equals x subscript n minus x subscript 0 equals 5

    • andspace straight capital delta x subscript i equals 5 over n

  • If the total interval starts at -3, then space x subscript 0 equals negative 3, space x subscript 1 equals negative 3 plus 5 over n,space x subscript 2 equals negative 3 plus 5 over n times 2, etc.

    • I.e.space a equals negative 3

    • b equals negative 3 plus 5 equals 2

    • and space x subscript i superscript italic ∗ equals negative 3 plus 5 over n i

  • This means Error converting from MathML to accessible text. can be interpreted as Error converting from MathML to accessible text.

    • I.e. f open parentheses x close parentheses equals x squared plus 1

  • Note that the sum is set up in the form of a right Riemann sum

    • I.e. with x subscript i superscript italic ∗ equals x subscript i

    • But as space straight capital delta x subscript i rightwards arrow 0 the type of Riemann sum used becomes insignificant

Recognizing all of this means the limit can be rewritten as a definite integral

Error converting from MathML to accessible text.

The value can be worked out by evaluating the definite integral

table row cell integral subscript negative 3 end subscript superscript 2 open parentheses x squared plus 1 close parentheses space d x end cell equals cell open square brackets x cubed over 3 plus x close square brackets subscript negative 3 end subscript superscript 2 end cell row blank equals cell open parentheses 2 close parentheses cubed over 3 plus open parentheses 2 close parentheses minus open parentheses open parentheses negative 3 close parentheses cubed over 3 plus open parentheses negative 3 close parentheses close parentheses end cell row blank equals cell 14 over 3 minus open parentheses negative 12 close parentheses end cell row blank equals cell 50 over 3 end cell end table

Error converting from MathML to accessible text.

Definite Integrals of sums, differences and constant multiples

What are the properties of sums, differences and constant multiples of definite integrals?

  • These are related to the equivalent properties for indefinite integrals

Definite integral of a constant times a function

  • If k is a constant, then

    • integral subscript a superscript b k f open parentheses x close parentheses space d x equals k integral subscript a superscript b f open parentheses x close parentheses space d x

      • I.e. the constant can be brought out in front of the integral as a multiplier

Definite integral of a sum or difference of functions

  • If f and g are two functions being integrated over the same interval, then

    • integral subscript a superscript b open parentheses f open parentheses x close parentheses plus-or-minus g open parentheses x close parentheses close parentheses space d x equals integral subscript a superscript b f open parentheses x close parentheses space d x plus-or-minus integral subscript a superscript b g open parentheses x close parentheses space d x

      • I.e. the integral of a sum (or difference) is equal to the sum (or difference) of integrals

Changing limits of integration

What are the definite integral properties involving integration limits?

  • There are three properties you should know here

Definite integral of a zero-length interval

  • For any function f

    • integral subscript a superscript a f open parentheses x close parentheses space d x equals 0

      • I.e. if the top and bottom integration limits are equal, the definite integral is equal to zero

Reversing the limits of integration

  • For a function f

    • integral subscript b superscript a f open parentheses x close parentheses space d x equals negative integral subscript a superscript b f open parentheses x close parentheses space d x

      • I.e. reversing the integration limits 'flips' the sign of the value of the definite integral

Definite integrals on adjacent intervals

  • For a function f, and for c such that a less or equal than c less or equal than b

    • integral subscript a superscript b f open parentheses x close parentheses space d x equals integral subscript a superscript c f open parentheses x close parentheses space d x plus integral subscript c superscript b f open parentheses x close parentheses space d x

      • I.e. the sum of definite integrals over adjacent subintervals of

        open square brackets a comma space b close square brackets is equal to the total definite integral from a to b

Worked Example

f is a function such that integral subscript 2 superscript 5 f open parentheses x close parentheses space d x equals negative 3 and integral subscript 2 superscript 7 f open parentheses x close parentheses space d x equals 12.

g is a function such that integral subscript 5 superscript 7 g open parentheses x close parentheses space d x equals 2.

Find the value of integral subscript 7 superscript 5 open parentheses f open parentheses x close parentheses minus 3 g open parentheses x close parentheses close parentheses space d x.

Answer:

First use the sum, difference and constant multiple properties

integral subscript 7 superscript 5 open parentheses f open parentheses x close parentheses minus 3 g open parentheses x close parentheses close parentheses space d x equals integral subscript 7 superscript 5 f open parentheses x close parentheses space d x minus 3 integral subscript 7 superscript 5 g open parentheses x close parentheses space d x

From the reversing the limits of integration property, we know that integral subscript 7 superscript 5 f open parentheses x close parentheses space d x equals negative integral subscript 5 superscript 7 f open parentheses x close parentheses space d x and integral subscript 7 superscript 5 g open parentheses x close parentheses space d x equals negative integral subscript 5 superscript 7 g open parentheses x close parentheses space d x

integral subscript 7 superscript 5 open parentheses f open parentheses x close parentheses minus 3 g open parentheses x close parentheses close parentheses space d x equals negative integral subscript 5 superscript 7 f open parentheses x close parentheses space d x plus 3 integral subscript 5 superscript 7 g open parentheses x close parentheses space d x

Use the adjacent intervals property to find integral subscript 5 superscript 7 f open parentheses x close parentheses space d x

table row cell integral subscript 2 superscript 7 f open parentheses x close parentheses space d x end cell equals cell integral subscript 2 superscript 5 f open parentheses x close parentheses space d x plus integral subscript 5 superscript 7 f open parentheses x close parentheses space d x end cell row blank blank blank row 12 equals cell negative 3 plus integral subscript 5 superscript 7 f open parentheses x close parentheses space d x end cell row blank blank blank row blank blank cell integral subscript 5 superscript 7 f open parentheses x close parentheses space d x equals 15 end cell end table

Now we have all the values we need

table row cell integral subscript 7 superscript 5 open parentheses f open parentheses x close parentheses minus 3 g open parentheses x close parentheses close parentheses space d x end cell equals cell negative integral subscript 5 superscript 7 f open parentheses x close parentheses space d x plus 3 integral subscript 5 superscript 7 g open parentheses x close parentheses space d x end cell row blank equals cell negative open parentheses 15 close parentheses plus 3 open parentheses 2 close parentheses end cell row blank equals cell negative 9 end cell end table

integral subscript 7 superscript 5 open parentheses f open parentheses x close parentheses minus 3 g open parentheses x close parentheses close parentheses space d x equals negative 9

Worked Example

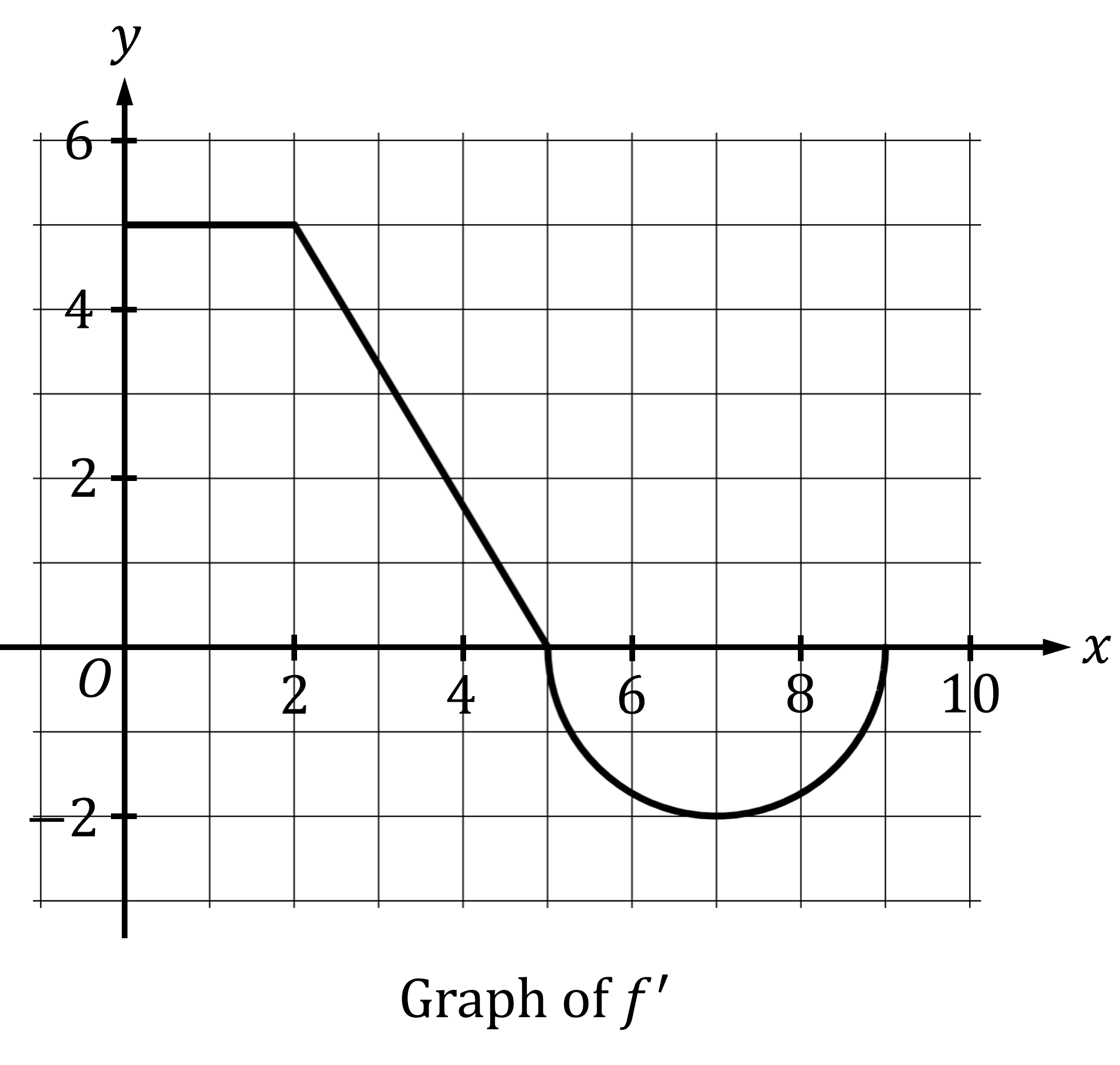
The graph of f', consisting of two straight line segments and a semicircle

The function f is defined on the closed interval open square brackets 0 comma space 9 close square brackets and satisfies f open parentheses 5 close parentheses equals negative 2. The graph of f to the power of apostrophe, the derivative of f, consists of two line segments and a semicircle, as shown in the figure.

Find

(a) space f open parentheses 9 close parentheses

Answer:

The value of f at 9 will be the value at 5, plus the accumulation of change between 5 and 9

f open parentheses 9 close parentheses equals f open parentheses 5 close parentheses plus integral subscript 5 superscript 9 f to the power of apostrophe open parentheses x close parentheses space d x

The integral of f to the power of apostrophe from 5 to 9 is the area of a semicircle of radius 2; but because f to the power of apostrophe is below the x-axis the value of the definite integral will be negative

table row cell f open parentheses 9 close parentheses end cell equals cell negative 2 plus open parentheses negative 1 half times pi open parentheses 2 close parentheses squared close parentheses end cell row blank equals cell negative 2 minus 2 pi end cell end table

f open parentheses 9 close parentheses equals negative 2 minus 2 pi

(b) space f open parentheses 0 close parentheses

Answer:

The value of f at 0 will be the value at 5, plus the accumulation of change between 5 and 0; i.e. going 'backwards' along the x-axis

f open parentheses 0 close parentheses equals f open parentheses 5 close parentheses plus integral subscript 5 superscript 0 f to the power of apostrophe open parentheses x close parentheses space d x

Use the 'reversing the limits of integration' property

f open parentheses 0 close parentheses equals f open parentheses 5 close parentheses minus integral subscript 0 superscript 5 f to the power of apostrophe open parentheses x close parentheses space d x

The integral of f to the power of apostrophe from 0 to 5 is the area of a rectangle of width 2 and height 5, and a right triangle of base 3 and height 5

table row cell f open parentheses 0 close parentheses end cell equals cell negative 2 minus open parentheses 2 times 5 plus 1 half times 3 times 5 close parentheses end cell row blank equals cell negative 2 minus 35 over 2 end cell row blank equals cell negative 39 over 2 end cell end table

f open parentheses 0 close parentheses equals negative 39 over 2

Last updated:

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Fundamental Theorem of CalculusNext:Evaluating Definite Integrals
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.