AP®MathsCollege BoardCalculus ABStudy GuidesUnit 6: Integration & Accumulation of ChangeRiemann Sums & Definite IntegralsFundamental Theorem of Calculus

Fundamental Theorem of Calculus (College Board AP® Calculus AB)

Study Guide

Test yourself
Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Fundamental theorem of calculus

What is the fundamental theorem of calculus?

  • The fundamental theorem of calculus is a key result in the study of calculus

    • It formalizes the idea that 'integration and differentiation are inverse operations'

    • and expresses several useful facts that follow on from this basic idea

  • There are two parts of the fundamental theorem that you should be familiar with and be able to use

    • The first fundamental theorem of calculus

    • and the second fundamental theorem of calculus

What is the first fundamental theorem of calculus?

  • The first fundamental theorem of calculus connects antiderivatives with the value of definite integrals

    • It provides a simple way to find the value of definite integrals

The first fundamental theorem of calculus

  • If

    • f is a function that is continuous on the closed interval open square brackets a comma space b close square brackets

    • and F is an antiderivative of f on open square brackets a comma space b close square brackets

  • Then

    • integral subscript a superscript b f open parentheses x close parentheses space d x equals F open parentheses b close parentheses minus F open parentheses a close parentheses

  • See the 'Evaluating Definite Integrals' study guide for details on how this is used

What is the second fundamental theorem of calculus?

  • The second fundamental theorem of calculus allows an antiderivative to be expressed in the form of an accumulation function

    • Recall that an accumulation function is a function of x where the variable x occurs as an integration limit:

      • E.g. space g open parentheses x close parentheses equals integral subscript a superscript x f open parentheses t close parentheses space d t

The second fundamental theorem of calculus

  • If

    • f is a function that is continuous on an interval containing a

  • Then for values of x in that interval

    • The function F defined by F open parentheses x close parentheses equals integral subscript a superscript x f open parentheses t close parentheses space d t is an antiderivative of f

    • and fraction numerator d over denominator d x end fraction open parentheses integral subscript a superscript x f open parentheses t close parentheses space d t close parentheses equals f open parentheses x close parentheses

Examiner Tips and Tricks

Be sure you are familiar with the implications of the second fundamental theorem!

Exam questions will probably not refer explicitly to the theorem, but they will expect you to recognize that:

  • integral subscript a superscript x f open parentheses t close parentheses space d t is an antiderivative of f

  • and especially that fraction numerator d over denominator d x end fraction open parentheses integral subscript a superscript x f open parentheses t close parentheses space d t close parentheses equals f open parentheses x close parentheses

Worked Example

The graph of a differentiable function f is shown below.

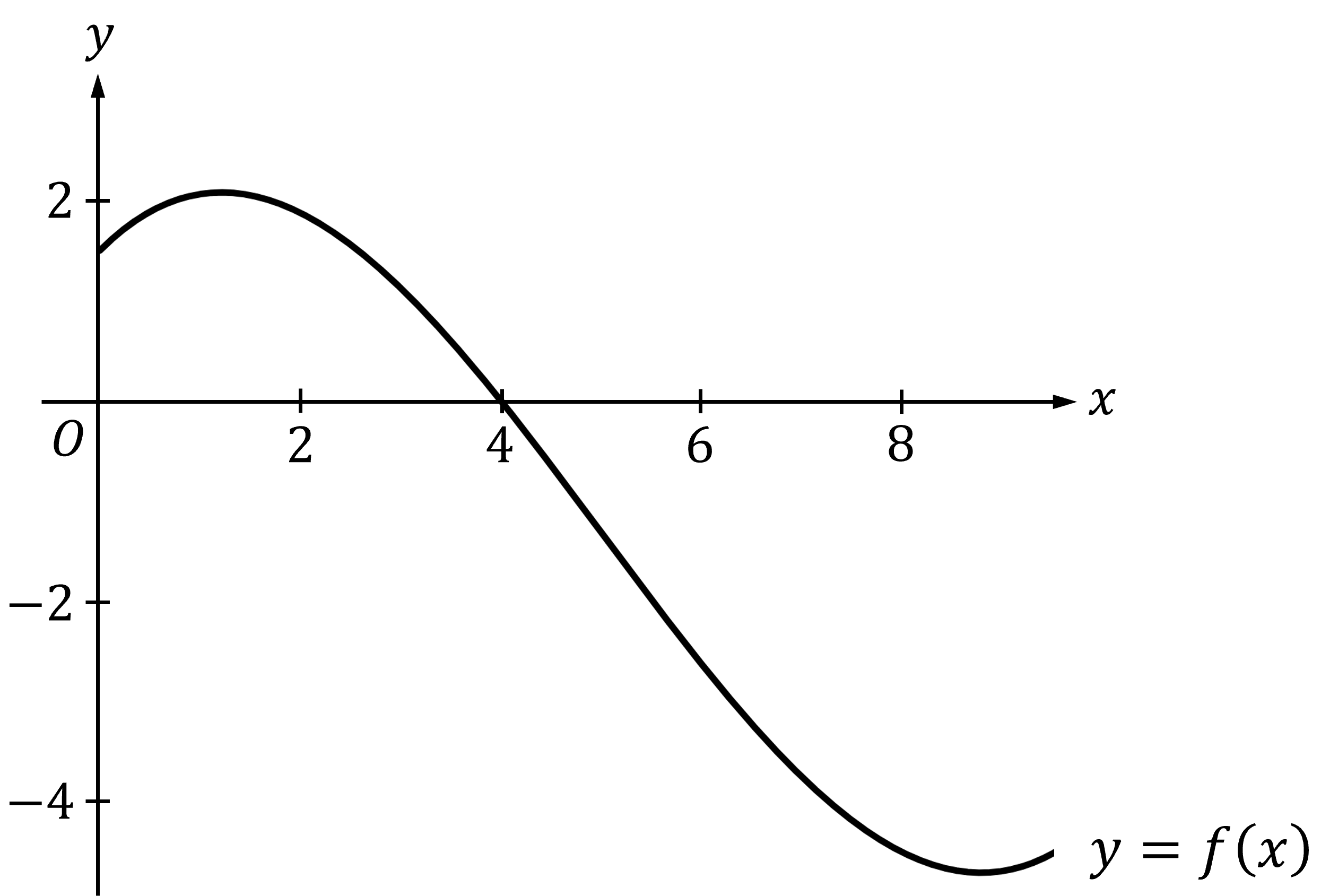
A graph of a function f(x), that is above the x-axis for x less than 4, crosses the x-axis at x=4, and then is below the x-axis for x greater than 4

If h open parentheses x close parentheses equals integral subscript 0 superscript x f open parentheses t close parentheses space d t, which of the following is true?

(A) space h open parentheses 4 close parentheses less than h to the power of apostrophe open parentheses 4 close parentheses less than h to the power of apostrophe apostrophe end exponent open parentheses 4 close parentheses

(B) space h open parentheses 4 close parentheses less than h to the power of apostrophe apostrophe end exponent open parentheses 4 close parentheses less than h to the power of apostrophe open parentheses 4 close parentheses

(C) space h to the power of apostrophe open parentheses 4 close parentheses less than h open parentheses 4 close parentheses less than h to the power of apostrophe apostrophe end exponent open parentheses 4 close parentheses

(D) space h to the power of apostrophe apostrophe end exponent open parentheses 4 close parentheses less than h open parentheses 4 close parentheses less than h to the power of apostrophe open parentheses 4 close parentheses

(E) space h to the power of apostrophe apostrophe end exponent open parentheses 4 close parentheses less than h to the power of apostrophe open parentheses 4 close parentheses less than h open parentheses 4 close parentheses

Answer:

We need to see what information we can deduce about h open parentheses 4 close parentheses, h to the power of apostrophe open parentheses 4 close parentheses and h to the power of apostrophe apostrophe end exponent open parentheses 4 close parentheses

h open parentheses 4 close parentheses equals integral subscript 0 superscript 4 f open parentheses t close parentheses space d t, which is calculating the accumulated change between 0 and 4

  • For those values, we can see from the graph that f is positive (i.e. above the x-axis)

  • So that means that space h open parentheses 4 close parentheses equals integral subscript 0 superscript 4 f open parentheses t close parentheses space d t greater than 0

h to the power of apostrophe open parentheses x close parentheses equals fraction numerator d over denominator d x end fraction open parentheses h open parentheses x close parentheses close parentheses equals fraction numerator d over denominator d x end fraction open parentheses integral subscript 0 superscript x f open parentheses t close parentheses space d t close parentheses

  • We are told that f is differentiable

    • Therefore f is continuous and the second fundamental theorem of calculus is valid

  • By the second fundamental theorem of calculus, fraction numerator d over denominator d x end fraction open parentheses integral subscript a superscript x f open parentheses t close parentheses space d t close parentheses equals f open parentheses x close parentheses

  • Therefore space h to the power of apostrophe open parentheses x close parentheses equals f open parentheses x close parentheses

  • So space h to the power of apostrophe open parentheses 4 close parentheses equals f open parentheses 4 close parentheses equals 0, as we can see from the graph

h to the power of apostrophe apostrophe end exponent open parentheses x close parentheses equals fraction numerator d over denominator d x end fraction open parentheses h to the power of apostrophe open parentheses x close parentheses close parentheses equals fraction numerator d over denominator d x end fraction open parentheses f open parentheses x close parentheses close parentheses equals f to the power of apostrophe open parentheses x close parentheses

  • From the graph we can see that f is a decreasing function in the vicinity of 4

  • Therefore space h to the power of apostrophe apostrophe end exponent open parentheses 4 close parentheses equals f to the power of apostrophe open parentheses 4 close parentheses less than 0

It follows that h to the power of apostrophe apostrophe end exponent open parentheses 4 close parentheses less than h to the power of apostrophe open parentheses 4 close parentheses less than h open parentheses 4 close parentheses

Option (E)

Last updated:

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Accumulation FunctionsNext:Properties of Definite Integrals
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.