AP®MathsCollege BoardCalculus ABStudy GuidesUnit 2: Differentiation Definition & Fundamental PropertiesDefinition of DifferentiationInstantaneous Rate of Change

Instantaneous Rate of Change (College Board AP® Calculus AB) : Study Guide

Jamie Wood

Written by: Jamie Wood

Reviewed by: Dan Finlay

Updated on

College Board Calculus ABCollege Board Calculus BC

Instantaneous rate of change

What is the instantaneous rate of change?

  • The instantaneous rate of change is the slope of a graph at a specific point, rather than between two points

  • Consider the graph of a function f with two points on the graph, A and B

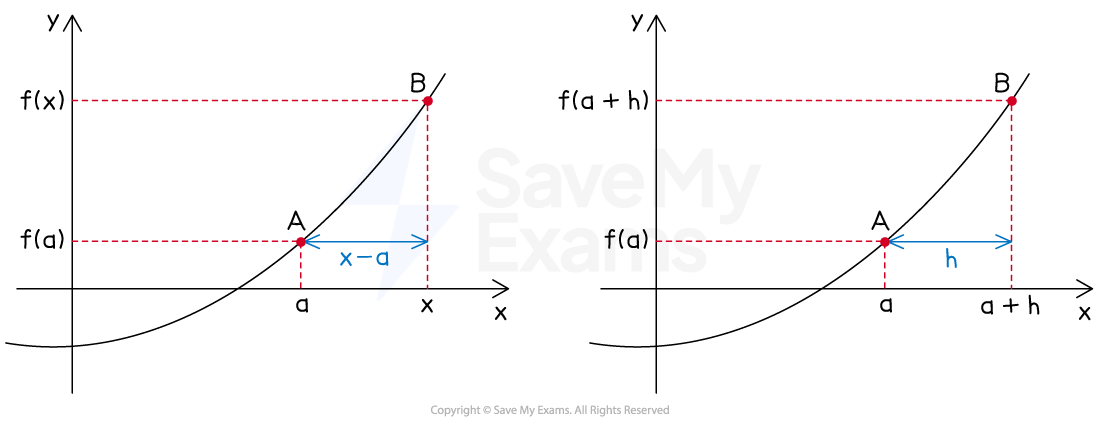
Two graphs showing a positive gradient curve with two points A and B. The left graph shows distance x-a; the right shows distance h between a and a+h.

  • Using the labeling on the left,

    • the average rate of change from A to B can be written as fraction numerator f open parentheses x close parentheses minus f open parentheses a close parentheses over denominator x minus a end fraction

  • Using the labeling on the right,

    • the average rate of change from A to B can be written as fraction numerator f open parentheses a plus h close parentheses minus f open parentheses a close parentheses over denominator h end fraction

  • To find the instantaneous rate of change, consider finding the slope between A and B as point B moves closer to point A

    • As the distance between the two points becomes smaller, the slope will become a more accurate estimate for the instantaneous rate of change at x equals a

    • Therefore the instantaneous rate of change will be the limit as this distance tends to zero

  • The instantaneous rate of change at x equals a can be written as

    • limit as x rightwards arrow a of fraction numerator f open parentheses x close parentheses minus f open parentheses a close parentheses over denominator x minus a end fraction or

    • limit as h rightwards arrow 0 of fraction numerator f open parentheses a plus h close parentheses minus f open parentheses a close parentheses over denominator h end fraction

  • These only give a valid answer if the relevant limit exists

  • They are both equivalent forms of the definition of the derivative of the function at x equals a, denoted by f to the power of apostrophe open parentheses a close parentheses

Worked Example

A function f open parentheses x close parentheses is defined by f open parentheses x close parentheses equals x squared.

Using the equation below, find the instantaneous rate of change of f open parentheses x close parentheses at the point where x equals 2.

f to the power of apostrophe open parentheses x close parentheses equals limit as h rightwards arrow 0 of fraction numerator f open parentheses x plus h close parentheses minus f open parentheses x close parentheses over denominator h end fraction

Answer:

Substitute x equals 2 into the given formula

f to the power of apostrophe open parentheses 2 close parentheses equals limit as h rightwards arrow 0 of fraction numerator f open parentheses 2 plus h close parentheses minus f open parentheses 2 close parentheses over denominator h end fraction

Evaluate the function, f open parentheses x close parentheses equals x squared, at x equals 2 plus h and x equals 2

f to the power of apostrophe open parentheses 2 close parentheses equals limit as h rightwards arrow 0 of fraction numerator open parentheses 2 plus h close parentheses squared minus open parentheses 2 close parentheses squared over denominator h end fraction

Expand and simplify the numerator

f to the power of apostrophe open parentheses 2 close parentheses equals limit as h rightwards arrow 0 of fraction numerator 4 plus 4 h plus h squared minus 4 over denominator h end fraction f to the power of apostrophe open parentheses 2 close parentheses equals limit as h rightwards arrow 0 of fraction numerator 4 h plus h squared over denominator h end fraction

Simplify the fraction by cancelling terms

f to the power of apostrophe open parentheses 2 close parentheses equals limit as h rightwards arrow 0 of open parentheses 4 plus h close parentheses

Evaluate the limit

f to the power of apostrophe open parentheses 2 close parentheses equals 4

👀 You've read 1 of your 5 free study guides this week
An illustration of students holding their exam resultsUnlock more study guides. It's free!

By signing up you agree to our Terms and Privacy Policy.

Already have an account? Log in

Test yourself

Did this page help you?

Previous:Average Rate of ChangeNext:Derivatives & Tangents
Author
Reviewer
Jamie Wood

Author: Jamie Wood

Expertise: Maths Content Creator

Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

Dan Finlay

Reviewer: Dan Finlay

Expertise: Maths Lead

Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

Download notes on Instantaneous Rate of Change