AP®MathsCollege BoardCalculus ABStudy GuidesUnit 2: Differentiation Definition & Fundamental PropertiesDefinition of DifferentiationDerivatives & Tangents

Derivatives & Tangents (College Board AP® Calculus AB)

Study Guide

Test yourself
Jamie Wood

Written by: Jamie Wood

Reviewed by: Dan Finlay

Derivatives and tangents

What is the derivative of a function?

  • The derivative of a function describes the instantaneous rate of change of a function at any given point

    • It is equal to the slope of the curve at that point

  • The derivative of the function f is defined by

    • f to the power of apostrophe open parentheses x close parentheses equals limit as h rightwards arrow 0 of fraction numerator f open parentheses x plus h close parentheses minus f open parentheses x close parentheses over denominator h end fraction

    • This is only valid for values of x where this limit exists

    • Note that the derivative is also a function of x

  • There are several ways to denote the derivative of f open parentheses x close parentheses

    • f to the power of apostrophe open parentheses x close parentheses

    • fraction numerator d y over denominator d x end fraction

    • y to the power of apostrophe

  • You may also see "the derivative of ..." written as " ... differentiated"

    • They mean the same thing

  • The value of the derivative of a function at a point is equal to the slope of the tangent to the graph at that point

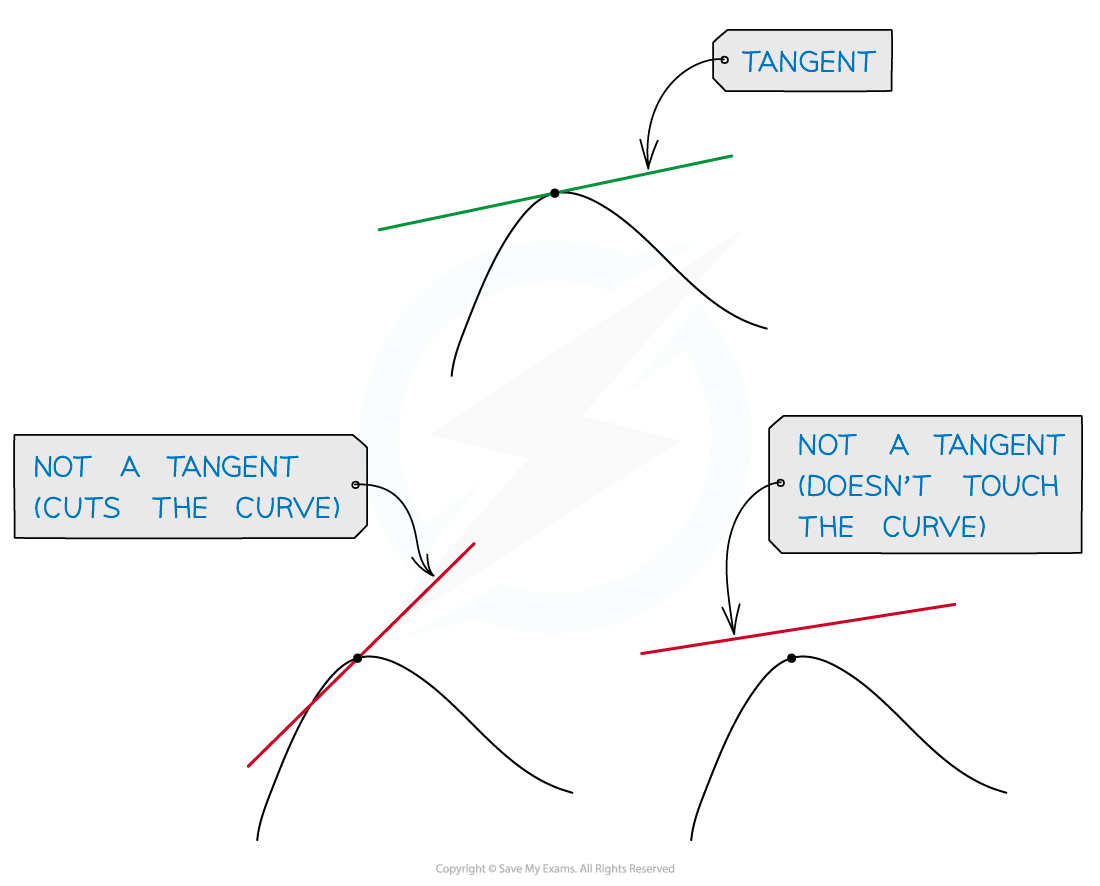
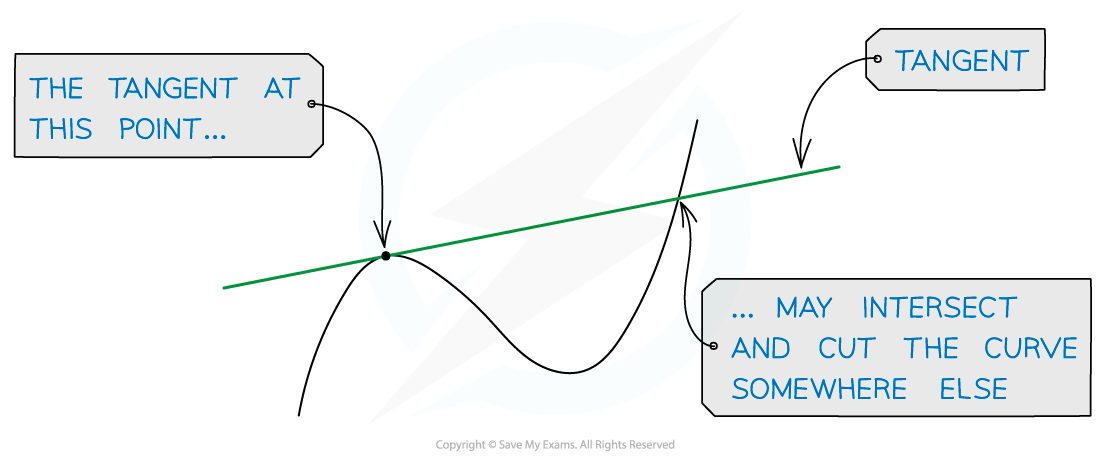
    • A tangent to a curve is a line that just touches the curve at one point but doesn't cut it at or near that point

      • However it may cut the curve somewhere else

Diagram showing examples of tangent lines to curves. Green line is a tangent touching the curve at one point. Red lines are not tangents; one cuts the curve, the other does not touch.
A graph showing a curve and a tangent line touching the curve at one point with labels explaining that the tangent may intersect and cut the curve elsewhere.

How do I find the equation of a tangent to a curve using a derivative?

  • To find the equation of a tangent line to the graph of a function f at the point open parentheses a comma b close parentheses using a derivative:

    • Represent the equation of the tangent using the general form for the equation of a straight line with slope m that goes through point open parentheses x subscript 1 comma space y subscript 1 close parentheses

      • y minus y subscript 1 equals m open parentheses x minus x subscript 1 close parentheses

    • Substitute in open parentheses a comma space b close parentheses as the point open parentheses x subscript 1 comma space y subscript 1 close parentheses

      • This is the point the tangent touches on the curve

    • Find the value of the derivative of f open parentheses x close parentheses at the point open parentheses a comma space b close parentheses if it is not given; this is f to the power of apostrophe open parentheses a close parentheses

      • The value of the derivative of f open parentheses x close parentheses at open parentheses a comma space b close parentheses is equal to the slope of the tangent at open parentheses a comma space b close parentheses

    • Substitute in f to the power of apostrophe open parentheses a close parentheses as the value of m in the equation of the tangent

    • The equation of the tangent will be of the form

      • y minus b equals f to the power of apostrophe open parentheses a close parentheses space open parentheses x minus a close parentheses

    • This equation can then be rearranged to another desired form if needed

      • For example, y equals b plus f to the power of apostrophe open parentheses a close parentheses space open parentheses x minus a close parentheses

When will tangent lines be horizontal or vertical?

  • The tangent line to the graph of a function f will be horizontal when f to the power of apostrophe open parentheses x close parentheses equals 0

    • Horizontal lines have a slope of zero

  • The tangent line to the graph of a function f will be vertical when f to the power of apostrophe open parentheses x close parentheses is undefined because of dividing a constant by zero

    • E.g. f open parentheses x close parentheses equals x to the power of 1 third end exponent with derivative f to the power of apostrophe open parentheses x close parentheses equals fraction numerator 1 over denominator 3 x to the power of 2 over 3 end exponent end fraction

      • f to the power of apostrophe open parentheses 0 close parentheses equals 1 over 0, which is undefined, even though f open parentheses x close parentheses is defined at x equals 0

      • Therefore the graph of f has a vertical tangent at x equals 0

    • But be careful, as there are other reasons a derivative might not be defined at a point

      • E.g. the derivative of g open parentheses x close parentheses equals open vertical bar x close vertical bar is undefined at x equals 0, because the left- and right-hand limits defining the derivative at that point are not equal

      • The graph of g does not have a vertical tangent (or any tangent) at that point

    • Also don't confuse vertical tangents with vertical asymptotes

      • Tangents and curves intersect, but curves only approach asymptotes without ever intersecting with them

      • E.g. h open parentheses x close parentheses equals 1 over x has a vertical asymptote at x equals 0

      • But the function is not defined when x equals 0, so it has no tangent at that point

Worked Example

Let the function f be defined by f open parentheses x close parentheses equals x squared minus 3 x minus 4. It is known that at the point where x equals 4, the instantaneous rate of change of f open parentheses x close parentheses is 5.

Find the equation of the line that is tangent to the graph of f at the point where x equals 4.

Answer:

The tangent is a straight line of the form y minus y subscript 1 equals m open parentheses x minus x subscript 1 close parentheses

The question states that the instantaneous rate of change (the slope) of the curve when x equals 4, is 5

f apostrophe open parentheses 4 close parentheses equals 5

This means the slope of the tangent, m, will also be 5 at this point

The x-coordinate of the point is known, but not the y value

open parentheses 4 comma space y subscript 1 close parentheses

Find the y value by substituting x equals 4 into f open parentheses x close parentheses

y subscript 1 equals f open parentheses 4 close parentheses equals 4 squared minus 3 open parentheses 4 close parentheses minus 4 equals 0

So the point where the tangent touches the curve is open parentheses 4 comma space 0 close parentheses

Substitute the point, and the slope at this point, into the equation of the tangent

y minus 0 equals 5 open parentheses x minus 4 close parentheses

Simplify

y equals 5 open parentheses x minus 4 close parentheses or y equals 5 x minus 20

Last updated:

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Instantaneous Rate of ChangeNext:Estimating the Derivative at a Point
    Author
    Reviewer
    Jamie Wood

    Author: Jamie Wood

    Expertise: Maths

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.