Average Rate of Change (College Board AP® Calculus AB)

Study Guide

Written by: Jamie Wood

Reviewed by: Dan Finlay

The average rate of change between two points on a graph, is the slope of the line segment joining the two points
The slope is equal to the change in $y$ -values, divided by the change in $x$ -values
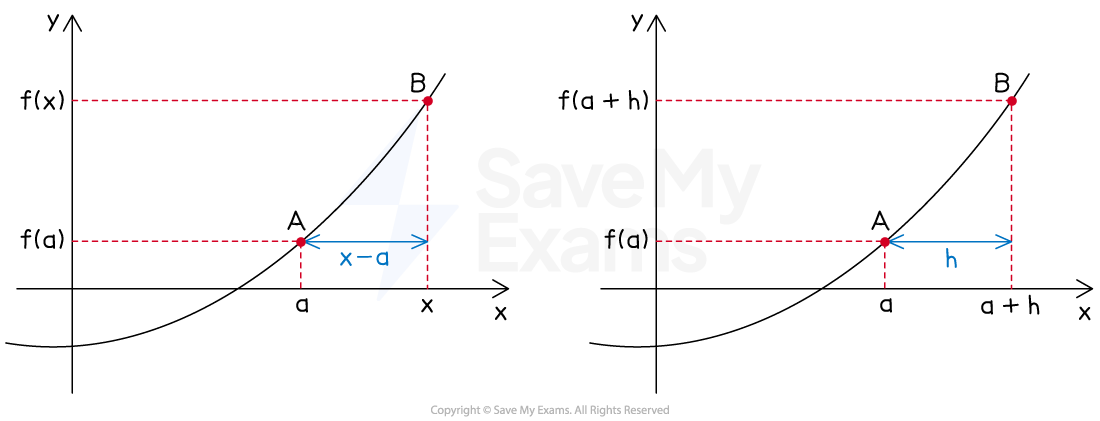
The average rate of change between $(x_{1}, y_{1})$ and $(x_{2}, y_{2})$ is therefore
- $\frac{y_{2} - y_{1}}{x_{2} - x_{1}}$
This means that the average rate of change is undefined at a point where the change in $x$ is zero for a given change in $y$

For a function $f$ ,
- a point with $x$ -coordinate $x$ will have $y$ -coordinate $f (x)$
- a point with $x$ -coordinate $a$ will have $y$ -coordinate $f (a)$
The average rate of change can therefore be written as
- $\frac{f (x) - f (a)}{x - a}$
If an $x$ -coordinate of $a$ is used for the first point, and the second point lies $h$ units to the right,
- the second point will have an $x$ -coordinate of $x + h$
The average rate of change can therefore also be written as
- $\frac{f (a + h) - f (a)}{h}$

Let $f$ be the function defined by $f (x) = 3 x^{3} + 2 x - 8$ .

Find the average rate of change between the point with an $x$ -coordinate of -1 and the point with an $x$ -coordinate of 2.

Answer:

The average rate of change between two points can found using $\frac{f (x) - f (a)}{x - a}$

$\frac{f (2) - f (- 1)}{2 - - 1}$

Evaluate the function at the two points and simplify

$\frac{(3 {(2)}^{3} + 2 (2) - 8) - (3 {(- 1)}^{3} + 2 (- 1) - 8)}{3}$

$\frac{(20) - (- 13)}{3}$

$\frac{33}{3}$

Simplify

Average rate of change = 11

Last updated: 6 August 2024

the (exam) results speak for themselves:

Did this page help you?