Introduction to Differential Equations (College Board AP® Calculus AB)

Revision Note

Author

Roger B

Expertise

Maths

Modeling with differential equations

What is a differential equation?

A differential equation is simply an equation that contains derivatives
- For example $\frac{d y}{d x} = 12 x y^{2}$ is a differential equation
- And so is $\frac{d^{2} x}{d t^{2}} - 5 \frac{d x}{d t} + 7 x = 5 \sin t$
It is an equation that includes both variables and rates of change of those variables

What is a first order differential equation?

A first order differential equation is a differential equation that contains first derivatives but no second (or higher) derivatives
- For example $\frac{d y}{d x} = 12 x y^{2}$ is a first order differential equation
- But $\frac{d^{2} x}{d t^{2}} - 5 \frac{d x}{d t} + 7 x = 5 \sin t$ is not a first order differential equation
  - because it contains the second derivative $\frac{d^{2} x}{d t^{2}}$

Why are differential equations useful for modeling?

Many quantities of interest in the real world involve rates of change
- For example:
  - The rate of change of a population of animals in a geographic area
  - The rate of change of the number of people infected by a particular disease
  - The rate of change of the amount of medication in a person's bloodstream at different times after ingestion
  - The rate of change of velocity for a falling object
  - The rate of change of voltage across a component in an electrical circuit
If the relationship between quantities and their rates of change can be written as a differential equation
- then solving the equation can allow us to predict the behavior of the quantities in the real world

General and particular solutions to differential equations

What is the difference between general and particular solutions for a differential equation?

The general solution to a differential equation may be thought of as 'every possible solution' to the differential equation
- E.g. $y^{2} = \frac{C - x^{2}}{4}$ is the general solution to $\frac{d y}{d x} = - \frac{x}{4 y}$
  - $C$ is an arbitrary constant (like a constant of integration)
- The general solution is actually an infinite family of solutions
  - Each one corresponding to a different value of $C$
- The graph of the solution will change depending on the value of $C$
  - This is shown in the diagram below:

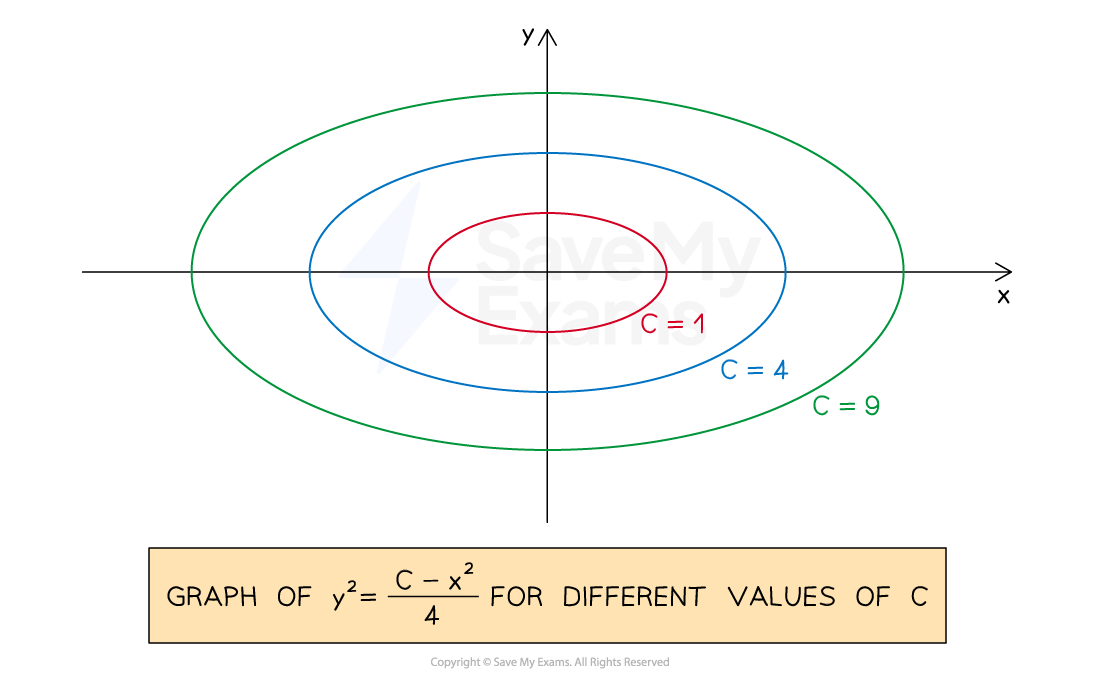
A graph shows nested ellipses corresponding to the equation y² = (C - x²)/4 with different values of C (1, 4, 9), centered at the origin, with labeled x and y axes.

The particular solution to a differential equation is
- the specific member of the general family of solutions
  - that satisfies the equation under a particular set of conditions
- E.g. if we know that $y = 1$ when $x = 0$
  - then $y^{2} = \frac{4 - x^{2}}{4}$ is the only solution that satisfies the differential equation with that set of conditions
- A condition like " $y = 1$ when $x = 0$ " is known as an initial condition (or boundary condition)
  - Finding a particular solution requires knowing an initial condition

Verifying solutions to differential equations

How can I use differentiation to verify solutions for a differential equation?

You can differentiate an answer to a differential equation to verify that it is indeed a solution
- E.g. verify that $y = 1 - x - \cos x$ is a solution to the differential equation $\frac{d y}{d x} = \sin x - 1$
  - Differentiate the proposed answer with respect to $x$
    - $\frac{d y}{d x} = \frac{d}{d x} (1 - x - \cos x) = - 1 + \sin x = \sin x - 1$
  - This matches the original differential equation
    - So the solution has been verified
For more complicated answers this may require the use of additional techniques
- E.g. implicit differentiation and/or substitution
- See the Worked Example

Worked Example

Verify that $y^{2} = \frac{1}{x^{2} + C}$ , where $C$ is an arbitrary constant, is a solution to the differential equation $\frac{d y}{d x} = - x y^{3}$ .

Answer:

Start by differentiating both sides of the proposed solution with respect to $x$ , using implicit differentiation

$\begin{array}{rcl} y^{2} & = & {(x^{2} + C)}^{- 1} \\ \frac{d}{d x} (y^{2}) & = & \frac{d}{d x} ({(x^{2} + C)}^{- 1}) \\ 2 y \frac{d y}{d x} & = & - {(x^{2} + C)}^{- 2} \cdot 2 x \\ 2 y \frac{d y}{d x} & = & - \frac{2 x}{{(x^{2} + C)}^{2}} \end{array}$

Rearrange to make $\frac{d y}{d x}$ the subject

$\begin{array}{rcl} \frac{d y}{d x} & = & - \frac{x}{y {(x^{2} + C)}^{2}} \end{array}$

This may not look like $\frac{d y}{d x} = - x y^{3}$

But remember that $y^{2} = \frac{1}{x^{2} + C}$

$\begin{array}{rcl} \frac{d y}{d x} & = & - \frac{x}{y} \cdot \frac{1}{{(x^{2} + C)}^{2}} \\ = & - \frac{x}{y} \cdot {(\frac{1}{x^{2} + C})}^{2} \\ = & - \frac{x}{y} \cdot {(y^{2})}^{2} \\ = & - \frac{x}{y} \cdot y^{4} \\ = & - x y^{3} \end{array}$

This confirms that $y^{2} = \frac{1}{x^{2} + C}$ is a solution

$y^{2} = \frac{1}{x^{2} + C}$ is a solution to the differential equation $\frac{d y}{d x} = - x y^{3}$

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Next topic

Did this page help you?