Related Rates (College Board AP® Calculus AB)

Study Guide

Test yourself

Written by: Jamie Wood

Reviewed by: Dan Finlay

Several rates of change can be linked together using the chain rule
The chain rule states that $\frac{d y}{d x} = \frac{d y}{d u} \times \frac{d u}{d x}$
This can be adapted or extended to other variables depending on the context

The most important part is forming an equation linking several rates together
Consider:
- Which rate are you trying to find?
- Which rates do you know?
- Which rates could you find (by differentiating)?
Remember that if you know, for example, $\frac{d y}{d x}$ , you can easily find $\frac{d x}{d y}$ by finding the reciprocal
- $\frac{d y}{d x} = \frac{1}{(\frac{d x}{d y})}$
Once you have formed the equation linking several rates, you should be able to substitute in known values to find an answer

How do I form an equation linking several rates?

Consider which rate you are trying to find
- E.g. "The rate of change of volume with respect to time" would be $\frac{d v}{d t}$
Consider the rates you know
- E.g. you may know the rate of change of height with respect to time, $\frac{d h}{d t}$
Consider the rates you can work out by differentiating
- E.g. you can work out the rate of change of volume with respect to height, $\frac{d v}{d h}$ , using a formula that links volume with height
It can help to list out all the rates
- $\frac{d v}{d t}, \frac{d h}{d t}, \frac{d v}{d h}$
Start with the rate you want to find, and leave blank spaces for rates that may help you find it
- $\frac{d v}{d t} = \frac{}{} \times \frac{}{}$
Fill in the numerator you are looking for in one of the blank numerators, and do the same for the denominator
- $\frac{d v}{d t} = \frac{d v}{} \times \frac{}{d t}$
Remember that all the terms other than these two, should cancel each other out
- This should give you some clues about which rates link together
In this example the related rates equation would be
- $\frac{d v}{d t} = \frac{d v}{d h} \times \frac{d h}{d t}$

An alternative method is to differentiate a known equation with respect to the variable you are interested in
For example if you have the equation $V = \frac{1}{3} π r^{3}$ ,
- and you need to find a rate linked with time, differentiate with respect to time as you would when using implicit differentiation
- $\frac{d V}{d t} = π r^{2} \frac{d r}{d t}$
Then substitute in the information you know to find the desired rate of change

Worked Example

The volume of a particular shape is given by $V = \frac{1}{3} π r^{3}$ , where $V$ is measured in meters cubed and $r$ is measured in meters.

Given that the rate of change of volume with respect to time is 7 meters cubed per minute, find the exact rate of change of $r$ with respect to time in meters per minute, at the time when $r$ is 2 meters.

Answer:

Identify the rate we are trying to find: the rate of change of $r$ with respect to $t$

$\frac{d r}{d t}$

Identify any rates we know

$\frac{d V}{d t} = 7$

Identify any rates we can work out, and find them
In this case we have a formula for $V$ in terms of $r$ , so we can find $\frac{d V}{d r}$

$V = \frac{1}{3} π r^{3}$

$\frac{d V}{d r} = π r^{2}$

Find an equation linking the rates

Start by writing down the rate we are trying to find, and fill in the numerator and denominator on the right hand side

$\frac{d r}{d t} = \frac{d r}{} \times \frac{}{d t}$

This structure should give you a clue as to how to arrange the other rates

We have $\frac{d V}{d t}$ , and we have $\frac{d V}{d r}$ so we therefore also have $\frac{d r}{d V}$ by finding the reciprocal

$\begin{array}{rcl} \frac{d r}{d t} & = & \frac{d r}{d V} \times \frac{d V}{d t} \\ = & \frac{1}{(\frac{d V}{d r})} \times \frac{d V}{d t} \end{array}$

Fill in the information we know

$\frac{d r}{d t} = \frac{1}{π r^{2}} \times 7$

We are asked to find the rate when $r = 2$ , so substitute this in to find the answer

$\frac{d r}{d t} = \frac{1}{π {(2)}^{2}} \times 7 = \frac{7}{4 π}$

The question asks for the rate as an exact value, so leave it in terms of $π$

$\frac{d r}{d t} = \frac{7}{4 π}$ meters per minute

An alternative method for this question is starting with the equation for the volume

$V = \frac{1}{3} π r^{3}$

Differentiate implicitly with respect to $t$ instead

$\frac{d V}{d t} = π r^{2} \frac{d r}{d t}$

And then substitute in the values of $\frac{d V}{d t}$ and $r$

$\begin{array}{rcl} 7 & = & π {(2)}^{2} \cdot \frac{d r}{d t} \\ \frac{d r}{d t} & = & \frac{7}{4 π} \end{array}$

$\frac{d r}{d t} = \frac{7}{4 π}$ meters per minute

The related rates equation may contain more than three terms
- E.g. $\frac{d v}{d t} = \frac{d v}{d r} \times \frac{d r}{d u} \times \frac{d u}{d t}$
- Just remember that all terms except the numerator and denominator you are looking for will cancel out
Any differentiating you need to do could involve
- Chain rule
- Product rule or quotient rule
- Implicit differentiation
- Known results e.g. Trigonometric functions or exponentials
Be careful with which variables are constant, and which are changing in a problem
- E.g. If a cone is shrinking, such as when liquid is leaking from a container,
  - then both the height of the cone, and the radius of the cone will be changing
- This means if you had to differentiate $V = \frac{1}{3} π r^{2} h$ with respect to either $r$ or $h$ ,
  - you would need to use the product rule and implicit differentiation
Drawing a diagram can help
- In particular look out for similar shapes
- E.g. When a cone shrinks, but retains its cone-shape, the ratio of the radius to the height will remain constant
- For a cone of height 20 and radius 5, the ratio of the radius to the height will always be 5:20
  - So if you know the height after a certain time, you can also work out the radius

Worked Example

A ladder is sliding down a long vertical wall. The ladder is 17 meters long, and the top is slipping down the wall at a rate of 6 meters per second. Find how fast the bottom of the ladder is moving along the ground when the bottom is 15 meters away from the wall.

Answer:

Label the change in height as $\frac{d y}{d t}$ , and note it will be negative as it is moving downwards

The hypotenuse will always remain as 17, as this is the length of the ladder

The speed at which the bottom of the ladder is moving away from the wall is $\frac{d x}{d t}$

Draw a diagram with this information

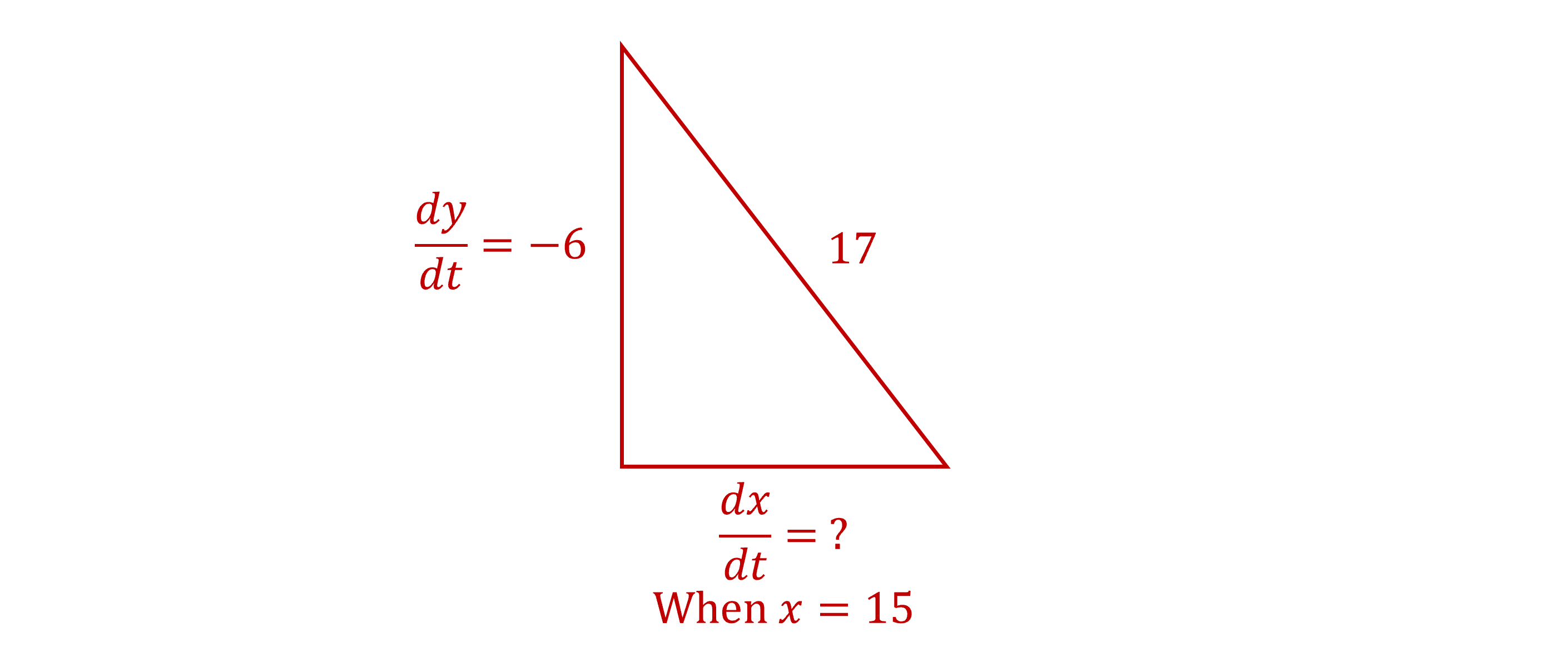
Right triangle with a hypotenuse of 17 units. Given dy/dt = -6, find dx/dt when x = 15.

Form an equation for $\frac{d x}{d t}$

$\frac{d x}{d t} = \frac{d x}{} \times \frac{}{d t} \frac{d x}{d t} = \frac{d x}{d y} \times \frac{d y}{d t}$

We already know $\frac{d y}{d t} = - 6$ , so we just need an expression for $\frac{d x}{d y}$

An expression linking $x$ and $y$ can be found by applying Pythagoras' theorem to the lengths in the diagram, as they form a right-angled triangle

$x^{2} + y^{2} = 17^{2} x^{2} + y^{2} = 289$

We can differentiate this to find an expression for $\frac{d x}{d y}$

Because $x$ and $y$ are both variable, implicit differentiation must be used to differentiate each term with respect to $y$

$\begin{array}{rcl} \frac{d}{d y} (x^{2}) + \frac{d}{d y} (y^{2}) & = & \frac{d}{d y} (289) \\ 2 x \cdot \frac{d x}{d y} + 2 y & = & 0 \\ \frac{d x}{d y} & = & \frac{- 2 y}{2 x} = - \frac{y}{x} \end{array}$

So we can now rewrite the equation linking the rates

$\frac{d x}{d t} = - \frac{y}{x} \times \frac{d y}{d t}$

We can also use Pythagoras to find $y$ when $x$ is 15

$\begin{array}{rcl} 15^{2} + y^{2} & = & 289 \\ y & = & 8 \end{array}$

When $x = 15$ , we now know that $y = 8$ , and we were told in the question that $\frac{d y}{d t} = - 6$

$\frac{d x}{d t} = - \frac{8}{15} \times - 6 \frac{d x}{d t} = \frac{16}{5} = 3.2$

3.2 metres per second

An alternative method for this question is starting with the equation linking the sides of the ladder

$x^{2} + y^{2} = 289$

Differentiate implicitly with respect to $t$ instead

$2 x \cdot \frac{d x}{d t} + 2 y \cdot \frac{d y}{d t} = 0$

And then substitute in the values of $x$ , $y$ , and $\frac{d y}{d t}$

$\begin{array}{rcl} 2 (15) \cdot \frac{d x}{d t} + 2 (8) \cdot (- 6) & = & 0 \\ \frac{d x}{d t} & = & 3.2 \end{array}$

3.2 metres per second

Last updated: 19 September 2024

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Motion in a Straight LineNext:Approximating Values of a Function

Related Rates (College Board AP® Calculus AB)

Study Guide

How do I form an equation linking several rates?

Worked Example

Worked Example

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Jamie Wood

Author: Dan Finlay

Related Rates (College Board AP® Calculus AB)

Study Guide

Solving related rates problems

What are related rates?

How do I solve a related rates problem?

How do I form an equation linking several rates?

How can I use implicit differentiation to solve a related rates problem?

What else should I be aware of in related rates questions?

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Jamie Wood

Author: Dan Finlay