Triangles as Cross Sections (College Board AP® Calculus AB)

Study Guide

Test yourself

Written by: Roger B

Reviewed by: Dan Finlay

Volumes with cross sections as triangles

How can I find the volume of a solid with a triangular cross section?

Use the basic concept
- If the area of the cross section of a solid is given by $A (x)$
  - and $A (x)$ is continuous on $[a, b]$
- Then the volume of the corresponding solid from $x = a$ to $x = b$ is
  - $Volume = \int_{a}^{b} A (x) d x$
You may need to create the cross sectional area function $A (x)$ based on information provided
- For example $A (x)$ may depend on the values of another function (or functions) given to you in the question
Remember that the area of a triangle is
- $Area = \frac{1}{2} \times base \times perpendicular height$

Worked Example

Let $R$ be the region enclosed by the graph of $f (x) = \sqrt{4 - x}$ and the $x$ - and $y$ -axes, as shown in the figure below.

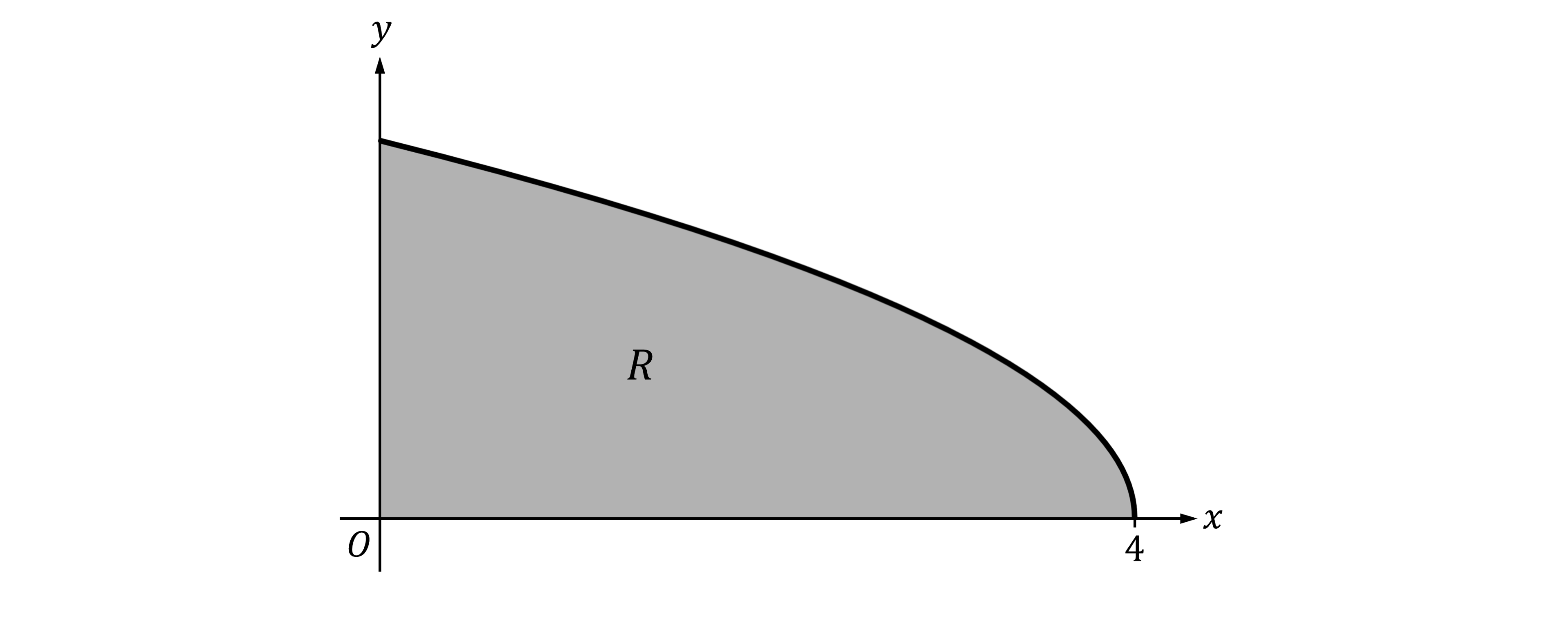
A shaded region labeled "R" is enclosed by the x-axis, the y-axis and the curve y=sqrt(4-x) from x=0 to x=4

Region $R$ is the base of a solid. For the solid, at each $x$ the cross section perpendicular to the $x$ -axis is an equilateral triangle. Find the volume of the solid.

Answer:

Use $Volume = \int_{a}^{b} A (x) d x$

Use Pythagoras' theorem to work out the relevant lengths in the cross section

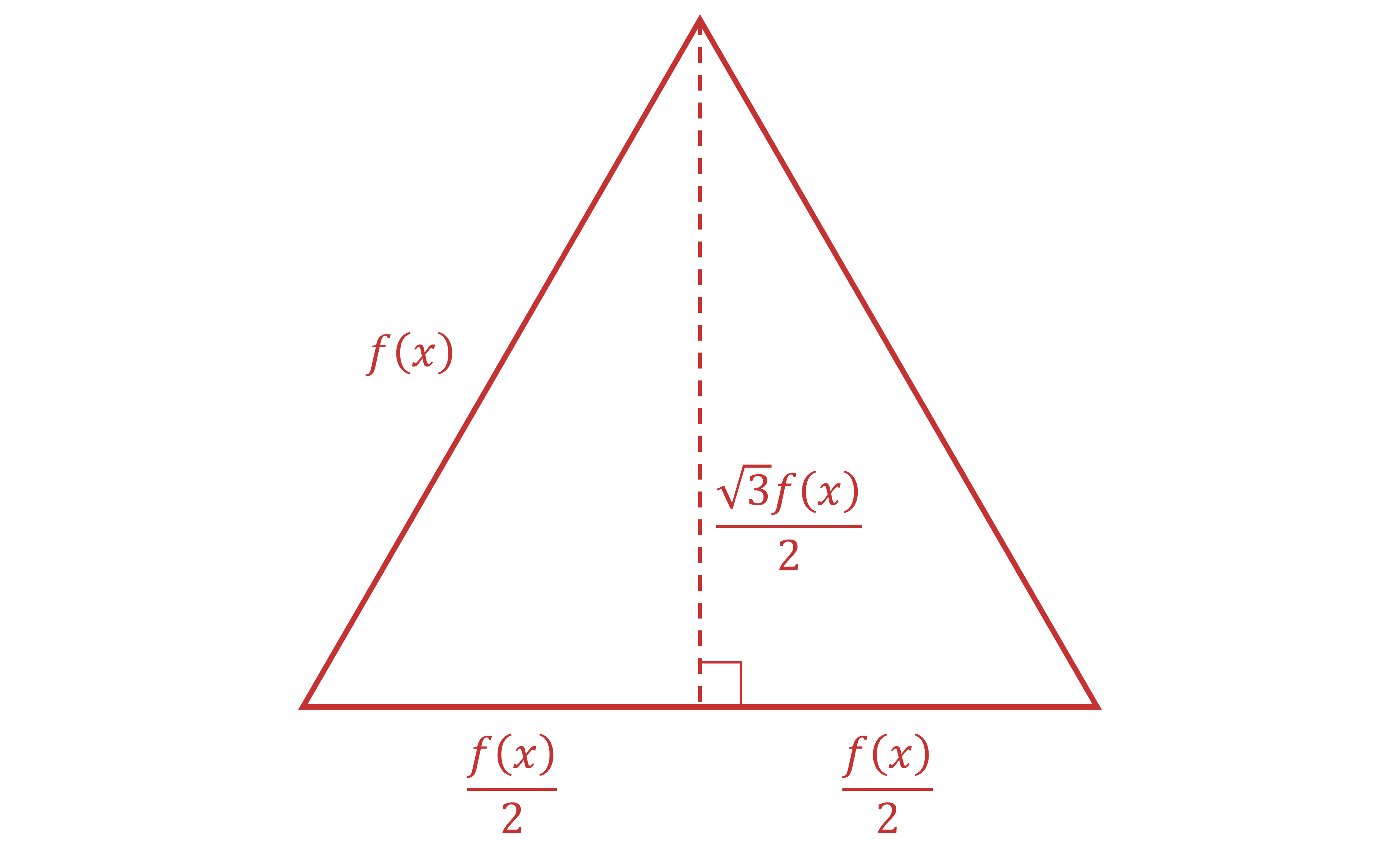
Equilateral triangle with side lengths of f(x), showing that the perpendicular height of the triangle is (sqrt(3)/2) * f(x)

$height = \sqrt{{(f (x))}^{2} - {(\frac{f (x)}{2})}^{2}} = \frac{\sqrt{3}}{2} f (x)$

At each $x$ the cross-sectional area is $\frac{1}{2} \times base \times height$

$A (x) = \frac{1}{2} \cdot f (x) \cdot \frac{\sqrt{3}}{2} f (x) = \frac{\sqrt{3}}{4} {(f (x))}^{2}$

Now the volume integral can be used

$\begin{array}{rcl} Volume & = & \int_{0}^{4} \frac{\sqrt{3}}{4} {(\sqrt{4 - x})}^{2} d x \\ = & \frac{\sqrt{3}}{4} \int_{0}^{4} (4 - x) d x \\ = & \frac{\sqrt{3}}{4} {[4 x - \frac{1}{2} x^{2}]}_{0}^{4} \\ = & \frac{\sqrt{3}}{4} ((4 (4) - \frac{1}{2} {(4)}^{2}) - (0)) \\ = & 2 \sqrt{3} \\ = & 3.464101 . . . \end{array}$

The question doesn't specify units, so the units of volume will be ${units}^{3}$

3.464 units³ (to 3 decimal places)

Last updated: 22 August 2024

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Rectangles as Cross SectionsNext:Semicircles as Cross Sections