AP®MathsCollege BoardCalculus ABRevision NotesUnit 8: Applications of IntegrationVolumes of RevolutionDisc Method Around Other Axes

Disc Method Around Other Axes (College Board AP® Calculus AB)

Revision Note

Roger B

Author

Roger B

Expertise

Maths

Volume with disc method revolving around other axes

How can I use the disc method to calculate volumes of revolution around axes parallel to the x-axis?

  • For a continuous function f, if the region bounded by

    • the curve y equals f open parentheses x close parentheses and the line y equals k

    • between x equals a and x equals b

  • is rotated 2 pi radians left parenthesis 360 degree right parenthesis around the line y equals k, then the volume of revolution is

    •  V equals pi integral subscript a superscript b open parentheses y minus k close parentheses squared space italic d x

      • Note that x here is a function of y

  • Thinking of this as an accumulation of change

    • pi open parentheses y minus k close parentheses squared times increment x is the volume of a disc with

      • circular cross section of radius open vertical bar y minus k close vertical bar

      • and length increment x

    • pi open parentheses y minus k close parentheses squared space d x is the limit of this volume element as increment x rightwards arrow 0

    • The integral integral subscript a superscript b pi open parentheses y minus k close parentheses squared space d x sums up all these infinitesimal volume elements between x equals a and x equals b

Worked Example

Let R be the region enclosed by the graph of f open parentheses x close parentheses equals 1 plus e to the power of negative x end exponent, the lines x equals 1 and x equals 3, and the line y equals negative 2, as shown in the figure below.

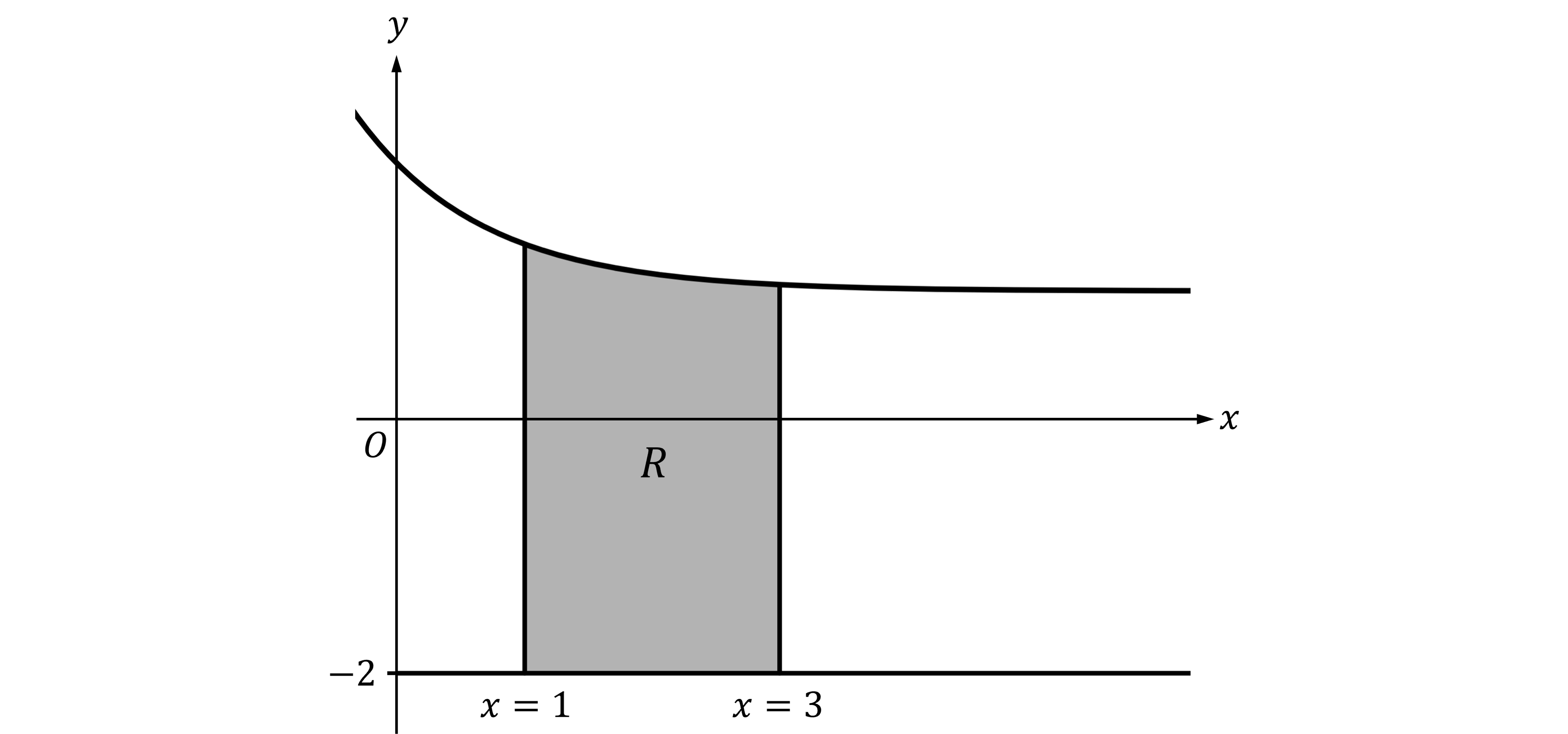
Graph showing a shaded region R bounded by the curve y=1+e^(-x) and the lines x=1, x=3, and y=-2

Find the volume of the solid generated when R is rotated about the horizontal line y equals negative 2.

Answer:

Use V equals pi integral subscript a superscript b open parentheses y minus k close parentheses squared space italic d x

table row V equals cell pi integral subscript 1 superscript 3 open parentheses open parentheses 1 plus e to the power of negative x end exponent close parentheses minus open parentheses negative 2 close parentheses close parentheses squared space italic d x end cell row blank equals cell pi integral subscript 1 superscript 3 open parentheses 3 plus e to the power of negative x end exponent close parentheses squared space italic d x end cell row blank equals cell pi integral subscript 1 superscript 3 open parentheses 9 plus 6 e to the power of negative x end exponent plus e to the power of negative 2 x end exponent close parentheses space italic d x end cell row blank equals cell pi open square brackets 9 x minus 6 e to the power of negative x end exponent minus 1 half e to the power of negative 2 x end exponent close square brackets subscript 1 superscript 3 end cell row blank equals cell pi open parentheses 18 minus 6 e to the power of negative 3 end exponent minus 1 half e to the power of negative 6 end exponent plus 6 e to the power of negative 1 end exponent plus 1 half e to the power of negative 2 end exponent close parentheses end cell row blank equals cell 62.753258... end cell end table

The question doesn't specify units, so the units of volume will be units cubed

62.753 units3 (to 3 decimal places)

How can I use the disc method to calculate volumes of revolution around axes parallel to the y-axis?

  • This is similar to finding volumes of revolution around axes parallel to the x-axis

  • For a continuous function f, if the region bounded by

    • the curve y equals f open parentheses x close parentheses and the line x equals k

    • between y equals a and y equals b

  • is rotated 2 pi radians left parenthesis 360 degree right parenthesis around the line x equals k, then the volume of revolution is

    •  V equals pi integral subscript a superscript b open parentheses x minus k close parentheses squared space italic d y

      • Note that x here is a function of y

        • This will mean rewriting y equals f open parentheses x close parentheses in the form x equals g open parentheses y close parentheses

      • Also note that the integration is done with respect to y

Worked Example

Let R be the region enclosed by the graph of f open parentheses x close parentheses equals ln open parentheses x minus 3 close parentheses, the lines y equals negative 2 and y equals 1, and the line x equals 1, as shown in the figure below.

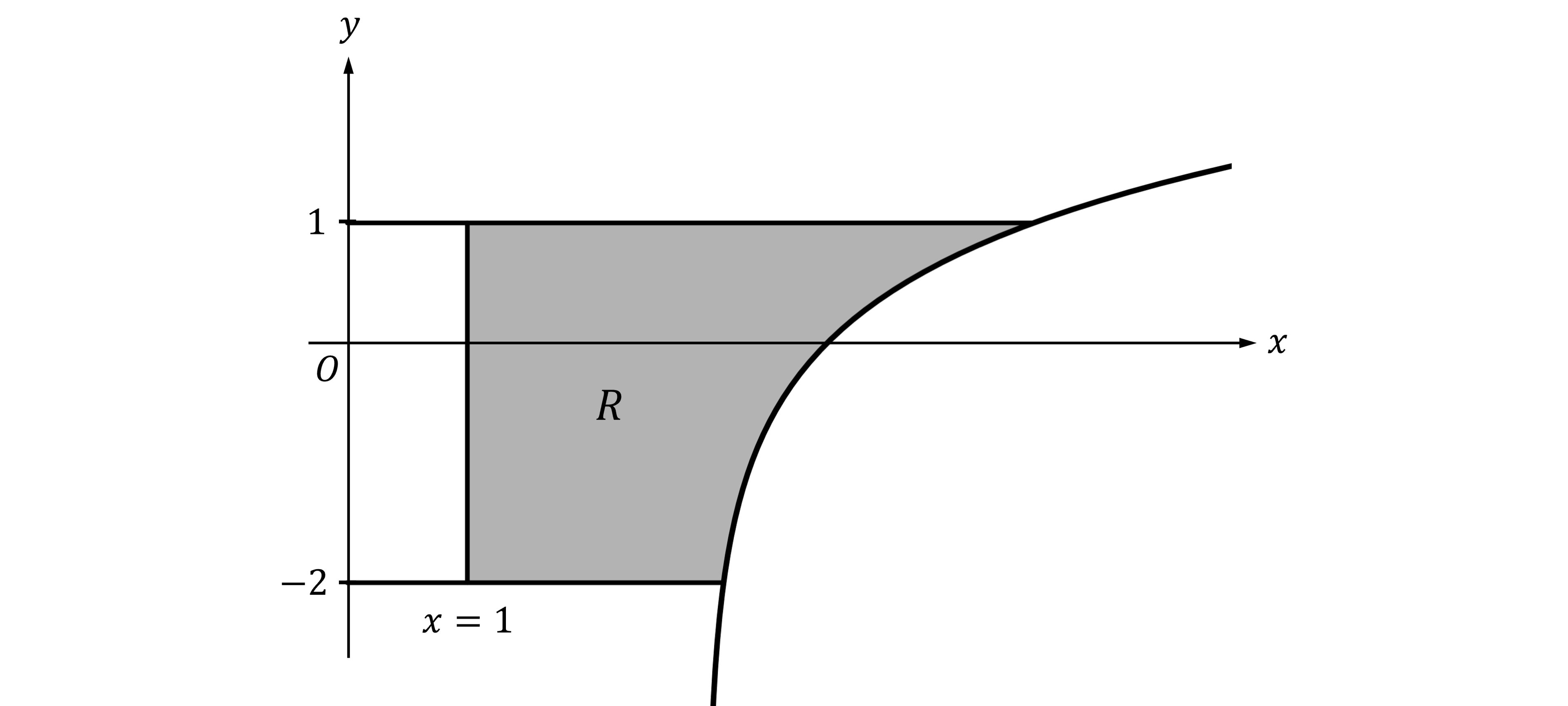
Graph depicting a shaded region R bounded by the curve y=ln(x-3), the lines y=-2 and y=-1, and the line x=1.

Find the volume of the solid generated when R is rotated about the vertical line x equals 1.

Answer:

Use V equals pi integral subscript a superscript b open parentheses x minus k close parentheses squared space italic d y

First rewrite the function as a function of y

table row y equals cell ln open parentheses x minus 3 close parentheses end cell row cell e to the power of y end cell equals cell x minus 3 end cell row x equals cell 3 plus e to the power of y end cell end table

Now that can be put into the integral

Note that the integration will be along the y-axis, from y equals negative 2 to y equals 1

table row V equals cell pi integral subscript negative 2 end subscript superscript 1 open parentheses open parentheses 3 plus e to the power of y close parentheses minus 1 close parentheses squared space italic d y end cell row blank equals cell pi integral subscript negative 2 end subscript superscript 1 open parentheses 2 plus e to the power of y close parentheses squared space italic d y end cell row blank equals cell pi integral subscript negative 2 end subscript superscript 1 open parentheses 4 plus 4 e to the power of y plus e to the power of 2 y end exponent close parentheses space italic d y end cell row blank equals cell pi open square brackets 4 x plus 4 e to the power of y plus 1 half e to the power of 2 y end exponent close square brackets subscript negative 2 end subscript superscript 1 end cell row blank equals cell pi open parentheses 12 plus 4 e plus 1 half e squared minus 4 e to the power of negative 2 end exponent minus 1 half e to the power of negative 4 end exponent close parentheses end cell row blank equals cell 81.735307...... end cell end table

The question doesn't specify units, so the units of volume will be units cubed

81.735 units3 (to 3 decimal places)

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Next topic

    Did this page help you?

    Roger B

    Author: Roger B

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.