Distance & Speed (College Board AP® Calculus AB)

Revision Note

Author

Jamie Wood

Expertise

Maths

Distance & speed as integrals

How are distance and speed different from displacement and velocity?

Distance is the magnitude of displacement, $|s|$
- Travelling 3 meters forwards and 3 meters backwards is a distance of 6 meters traveled
- But the displacement after this motion would be zero
Speed is the magnitude of velocity, $|v|$
- Travelling at 10 meters per second forward is a velocity of +10 meters per second
- Travelling at 10 meters per second backwards is a velocity of -10 meters per second
- In both these cases however, the speed is 10 meters per second

How do I find a distance using integration?

The total distance traveled between times $t_{1}$ and $t_{2}$ is given by $\int_{t_{1}}^{t_{2}} |v (t)| d t$
- This is because even when the object is moving backwards (negative velocity), the distance traveled is increasing (whilst the displacement is decreasing)
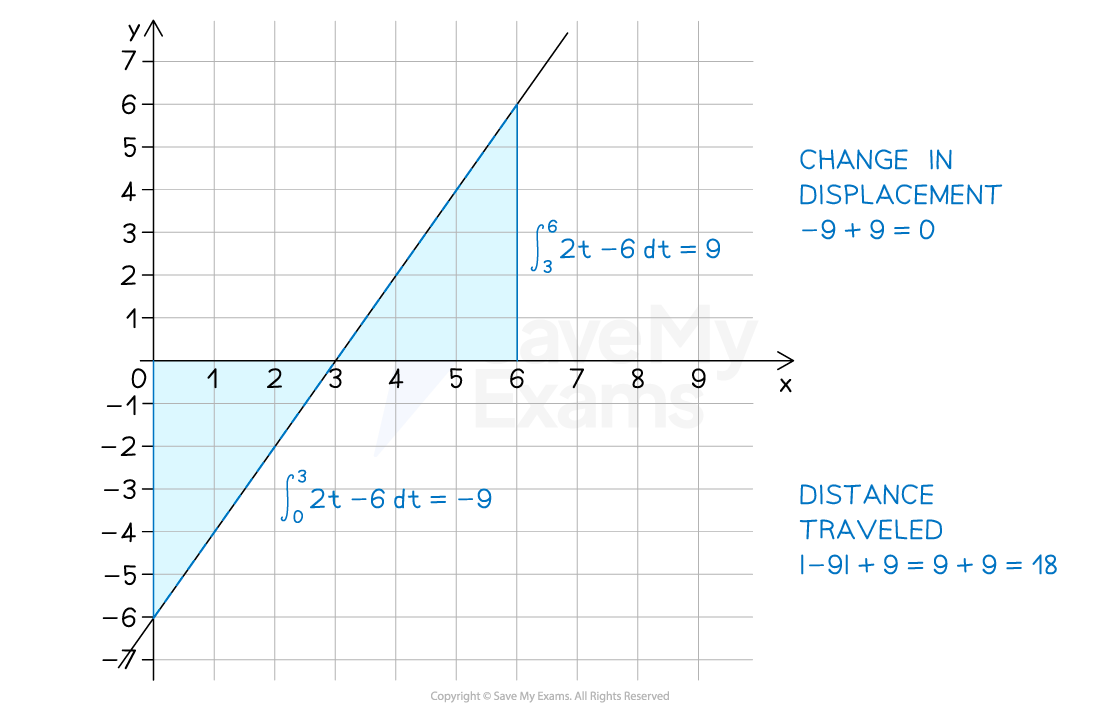
Consider a simple example, where $v = 2 t - 6$
- To find the change in displacement between $t = 0$ and $t = 6$ we would calculate
  - $\int_{0}^{6} 2 t - 6 d t$ , which has a value of zero
  - This is because $\int_{0}^{3} 2 t - 6 d t = - 9$ and $\int_{3}^{6} 2 t - 6 d t = + 9$
- To find the distance traveled between $t = 0$ and $t = 6$ we would calculate
  - $\int_{0}^{6} |2 t - 6| d t$ , which has a value of 18
  - You could find this on your calculator directly, using the "absolute" (i.e. absolute value or modulus) function
  - Alternatively you can sketch a velocity-time graph to find where the area under the graph would be negative and positive, and split the calculation into two integrals
  - Then make any negative integrals positive
    - $\int_{0}^{6} |2 t - 6| d t = |\int_{0}^{3} 2 t - 6 d t| + \int_{3}^{6} 2 t - 6 d t = |- 9| + 9 = 18$

Graph of velocity (v) versus time (t) with shaded areas representing integrals from 0 to 3 and 3 to 6. Text: Change in displacement is 0, Distance traveled is 18.

How does using speed rather than velocity affect calculations?

Pay close attention to whether a question refers to speed or velocity
This is important when a calculation involving velocity "goes through zero"
E.g. If a particle with velocity 5 meters per second decreases its velocity by 20 meters per second
- Its new velocity is -15 meters per second
- However its new speed is 15 meters per second
If a particle with velocity -8 meters per second, increases its velocity by 10 meters per second
- Its new velocity is 2 meters per second
- Its new speed is also 2 meters per second
- But, it has changed from a speed of 8 meters per second, to a speed of 2 meters per second
  - So it is true to say its speed has decreased by 6 meters per second
To find a change in velocity, leading to a calculation similar to above, you may need to integrate an expression for acceleration

Worked Example

The acceleration of a particle over the interval $0 \leq t \leq 6 π$ is described by the function $a (t) = \frac{3}{2} \cos (\frac{t}{2})$ where $v$ is measured in feet per second and $t$ is measured in seconds.

At $t = 0$ , the particle is at rest.

(a) Calculate the change in speed between $t = \frac{3 π}{2}$ and $t = 3 π$ . State if this is an increase or decrease.

Answer

Start by finding an expression for the velocity by integrating the expression for the acceleration

$\begin{array}{rcl} v (t) & = & \int a (t) d t = \int \frac{3}{2} \cos (\frac{t}{2}) d t \\ v (t) & = & 3 \sin \frac{t}{2} + C \end{array}$

To find the constant of integration, substitute in a known velocity at a point in time

We were told in the question the initial velocity is zero, so $v = 0$ when $t = 0$

$\begin{array}{rcl} 0 & = & 3 \sin (0) + C \\ 0 & = & 0 + C \\ C & = & 0 \end{array}$

$\begin{array}{rcl} v (t) & = & 3 \sin \frac{t}{2} \end{array}$

Find the velocities at $t = \frac{3 π}{2}$ and $t = 3 π$

$\begin{array}{rcl} v (\frac{3 π}{2}) & = & 3 \sin \frac{3 π}{4} = 2.12132034 . . . \end{array}$

$\begin{array}{rcl} v (3 π) & = & 3 \sin \frac{3 π}{2} = - 3 \end{array}$

Consider these results in terms of speeds rather than velocities

Speed at $t = \frac{3 π}{2}$ is $2.121320344 . . .$

Speed at $t = 3 π$ is 3

Therefore the speed has increased

Increase in speed = $3 - 2.12132034 . . . = 0.878679656 . . .$

Round to 3 decimal places

The speed has increased by 0.879 feet per second

(b) Find the total distance traveled by the particle between $t = π$ and $t = 4 π$ .

Answer:

Distance traveled will be $\int_{π}^{4 π} |v (t)| d t = \int_{π}^{4 π} |3 \sin \frac{t}{2}| d t$

On a calculator question you could use your calculator to evaluate this

If doing it by hand, you have to be careful with negative areas (i.e. intervals where $v (t) < 0$ )

The graph of $v = 3 \sin \frac{t}{2}$ will intersect the horizontal axis at $0, 2 π, 4 π, 6 π, . . .$ , so the area between $π$ and $4 π$ will have a positive and a negative portion

Split the integral into multiple parts, with the horizontal axis intercepts as the boundaries

$\begin{array}{rcl} \int_{π}^{2 π} 3 \sin \frac{t}{2} d t & = & {[- 6 \cos \frac{t}{2}]}_{π}^{2 π} \\ = & - 6 \cos π - (- 6 \cos \frac{π}{2}) \\ = & - 6 (- 1) - (0) \\ = & 6 \end{array}$

$\begin{array}{rcl} \int_{2 π}^{4 π} 3 \sin \frac{t}{2} d t & = & {[- 6 \cos \frac{t}{2}]}_{2 π}^{4 π} \\ = & - 6 \cos 2 π - (- 6 \cos π) \\ = & - 6 (1) - (- 6 (- 1)) \\ = & - 6 - 6 \\ = & - 12 \end{array}$

Find the total distance travelled by considering the absolute values of the changes in displacement

I.e. $distance traveled = \int_{π}^{4 π} |3 \sin \frac{t}{2}| d t = \int_{π}^{2 π} 3 \sin \frac{t}{2} d t + |\int_{2 π}^{4 π} 3 \sin \frac{t}{2} d t|$

6 + 12 = 18

Distance of 18 feet traveled between $t = π$ and $t = 4 π$

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Next topic

Did this page help you?