Multiple Areas (College Board AP® Calculus AB)

Study Guide

Test yourself

Written by: Roger B

Reviewed by: Dan Finlay

Using multiple definite integrals to find multiple areas

How do I find areas of enclosed regions partly above and partly below the x-axis using multiple integrals?

If an area between a curve and the $x$ -axis is partly above and partly below the $x$ -axis
- then you need to be careful when calculating areas
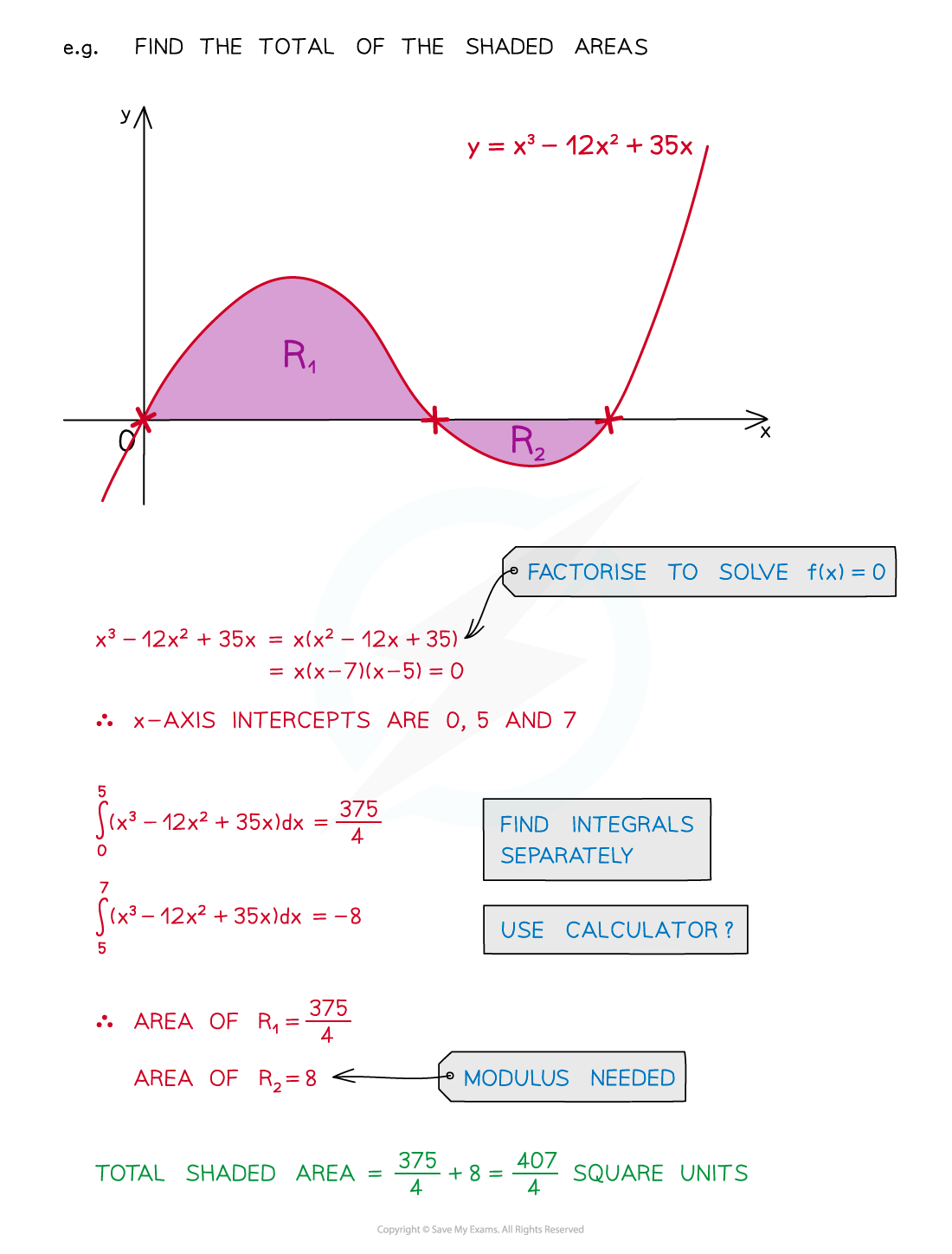
Consider the diagram below

Graph of the function f(x) with areas R1 and R2 shaded between points a, b, and c on the x-axis. R1 is above the x-axis and R2 is below the x-axis. Includes a mathematical explanation in a grey box of how to calculate the areas using definite integrals.

The total area cannot be found using $\int_{a}^{c} f (x) d x$
- Instead find $\int_{a}^{b} f (x) d x$
- and add the modulus (absolute value) of $\int_{b}^{c} f (x) d x$
  - I.e. $total area = \int_{a}^{b} f (x) d x + |\int_{b}^{c} f (x) d x|$
In general, calculate areas above and below the axis separately
- Add together the integrals for the areas above
- and the modulus of the integrals for the areas below
For example, to find the total area of the regions enclosed by the $x$ -axis and the curve $y = x^{3} - 12 x^{2} + 35 x$ :

An example of using integrals to work out the area between the x-axis and the curve y=x^3-12x^2+35x. The area is broken into two regions: region R1 above the x-axis, and region R2 below the x-axis.

How do I find total areas between two curves using multiple integrals?

If curves intersect at more than two points
- then you need to be careful when calculating the total area they enclose

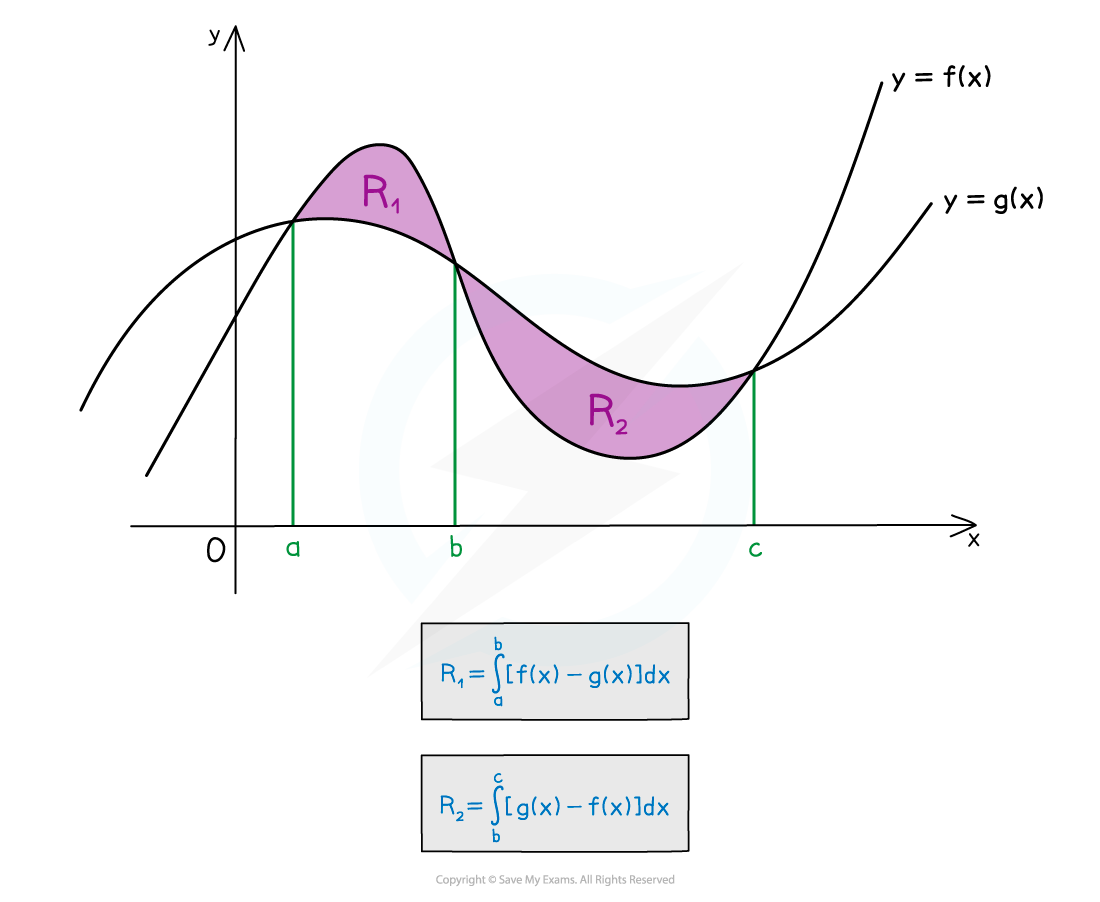
Graph showing areas between curves f(x) and g(x) from a to b (labeled region R1) and b to c (labeled region R2). Integrals for R1 and R2 are given below the graph.

Calculate areas of different regions separately
- In the integral for each region
  - make sure the 'bottom' function (closer to the $x$ -axis)
  - is being subtracted from the 'top' function (further from the $x$ -axis)

Worked Example

The shaded region in the diagram below is the region enclosed by the curves with equations $y = f (x)$ and $y = g (x)$ where

$f (x) = (x - 2) {(x - 3)}^{2}$

$g (x) = x^{2} - 5 x + 6$

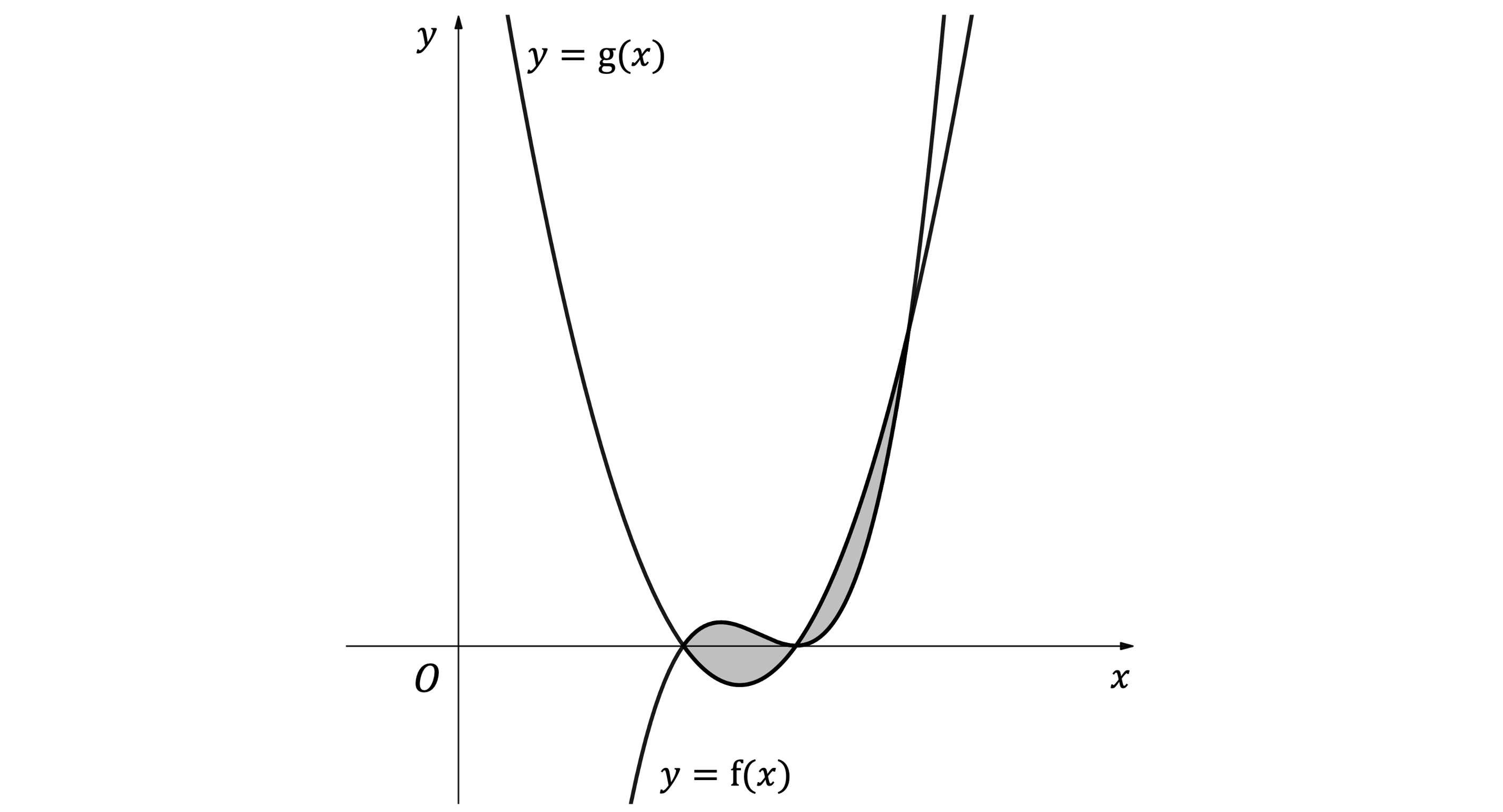
Graph showing the functions y=f(x) and y=g(x) intersecting, with a two-part shaded region between them.

Find the total area of the shaded region.

Answer:

Note first of all that for calculating areas between two curves, it doesn't matter that the areas are partially above and partially below the $x$ -axis

Start by finding the $x$ -values of the points of intersection of the two curves

$\begin{array}{rcl} f (x) & = & g (x) \\ (x - 2) {(x - 3)}^{2} & = & x^{2} - 5 x + 6 \\ (x - 2) {(x - 3)}^{2} & = & (x - 2) (x - 3) \end{array}$

This can be solved by moving everything to one side of the equation and factorizing further

$\begin{array}{rcl} (x - 2) {(x - 3)}^{2} - (x - 2) (x - 3) & = & 0 \\ (x - 2) (x - 3) ((x - 3) - 1) & = & 0 \\ (x - 2) (x - 3) (x - 4) & = & 0 \end{array}$

$x = 2, x = 3, x = 4$

Those will be the integration limits for the two integrals we need

Between $x = 2$ and $x = 3$ , $y = f (x)$ is the 'top' function, so

$\begin{array}{rcl} \int_{2}^{3} (f (x) - g (x)) d x & = & \int_{2}^{3} ((x - 2) {(x - 3)}^{2} - (x^{2} - 5 x + 6)) d x \\ = & \int_{2}^{3} (x^{3} - 9 x^{2} + 26 x - 24) d x \\ = & {[\frac{1}{4} x^{4} - 3 x^{3} + 13 x^{2} - 24 x]}_{2}^{3} \\ = & (\frac{81}{4} - 81 + 117 - 72) - (4 - 24 + 52 - 48) \\ = & \frac{1}{4} \end{array}$

That is the area for the part of the region on the left

Between $x = 3$ and $x = 4$ , $y = g (x)$ is the 'top' function, so

$\begin{array}{rcl} \int_{3}^{4} (g (x) - f (x)) d x & = & \int_{3}^{4} ((x^{2} - 5 x + 6) - (x - 2) {(x - 3)}^{2}) d x \\ = & \int_{3}^{4} (- x^{3} + 9 x^{2} - 26 x + 24) d x \\ = & {[- \frac{1}{4} x^{4} + 3 x^{3} - 13 x^{2} + 24 x]}_{3}^{4} \\ = & (- 64 + 192 - 208 + 96) - (- \frac{81}{4} + 81 - 117 + 72) \\ = & \frac{1}{4} \end{array}$

That is the area for the part of the region on the right

Add together to get the total area

$\frac{1}{4} + \frac{1}{4} = \frac{1}{2}$

The total area is $\frac{1}{2}$ units squared

Using absolute value to find multiple areas

How do I find areas of regions partly above and partly below the x-axis using absolute value?

If you are using your calculator to work out area integrals you can use
- $Area = \int_{a}^{b} |f (x)| d x$
  - I.e. integrate the absolute value (modulus) of the function
This will find the area
- between the curve $y = f (x)$ and the $x$ -axis
- between $x = a$ and $x = b$
Because the absolute value changes any negative parts of $f (x)$ into their positive equivalents
- you don't need to worry about different parts of the area being above or below the $x$ -axis

Examiner Tips and Tricks

Even if you are using your calculator to work out the value of an integral on the exam

you should write down the integral you are evaluating, to make sure your answer gets full credit

Worked Example

The shaded region in the diagram below is the region enclosed by the $x$ -axis and the graph of the function $y = x^{3} - 12 x^{2} + 35 x$ .

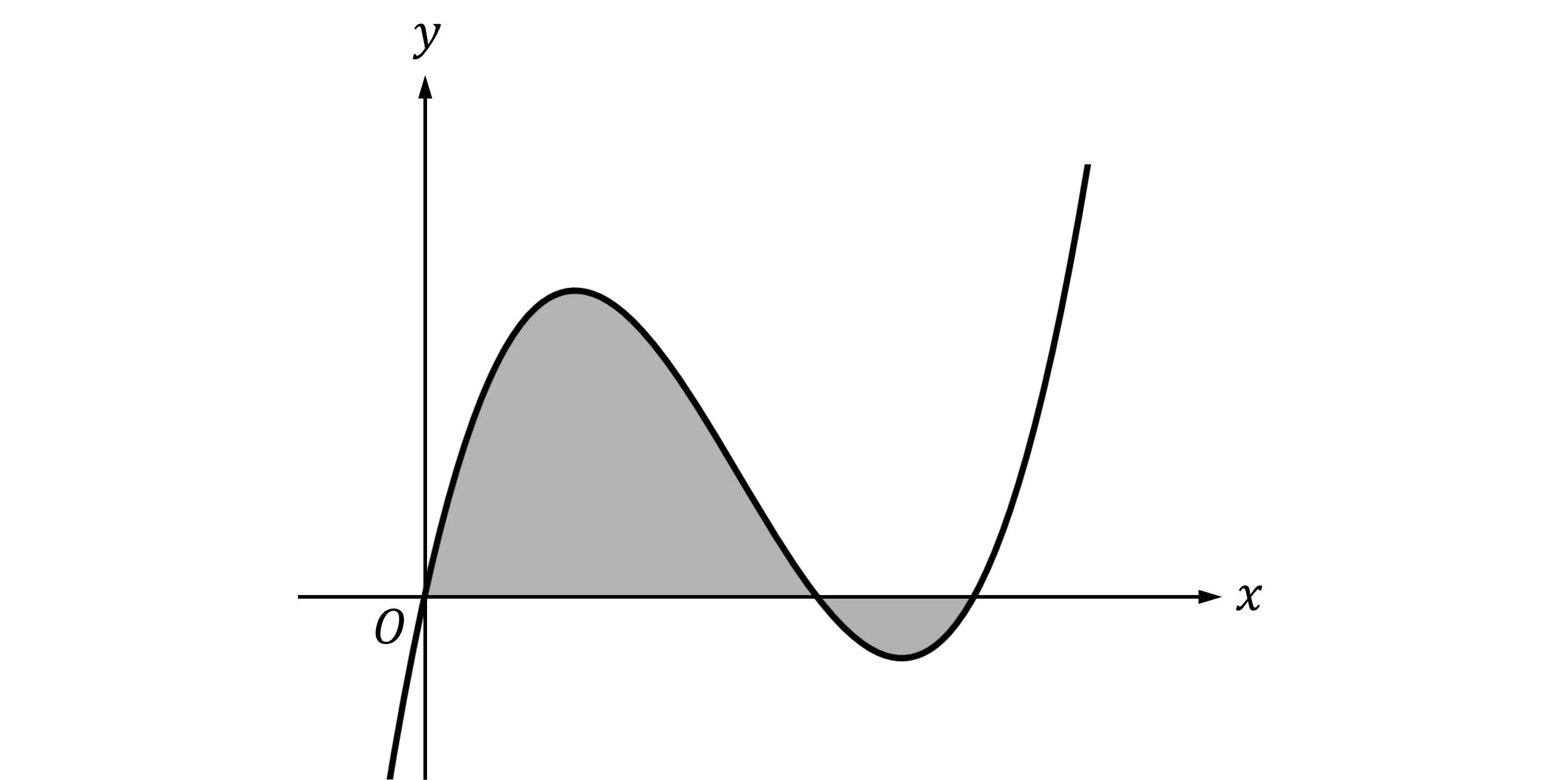
Graph showing a shaded area enclosed by a curve and the x-axis. Part of the area is below the x-axis, and part of it is above the x-axis.

Find the total area of the shaded region.

Answer:

Start by finding the points where the graph intersects the $x$ -axis

$\begin{array}{rcl} x^{3} - 12 x^{2} + 35 x & = & 0 \\ x (x - 5) (x - 7) & = & 0 \end{array}$

$x = 0, x = 5, x = 7$

To work this out by hand we'd need to find the two areas separately, between $x = 0$ and $x = 5$ (the bit above the $x$ -axis), and between $x = 5$ and $x = 7$ (the bit below the $x$ -axis)

Instead we can work out the entire area between $x = 0$ and $x = 7$ with one integral using absolute value

$Area = \int_{0}^{7} |x^{3} - 12 x^{2} + 35 x| d x$

That integral can be evaluated using your graphing calculator

$\begin{array}{rcl} \int_{0}^{7} |x^{3} - 12 x^{2} + 35 x| d x & = & \frac{407}{4} = 101.75 \end{array}$

Total area = 101.75 units squared

How do I find total areas between two curves using absolute value?

If you are using your calculator to work out area integrals you can use
- $Area = \int_{a}^{b} |f (x) - g (x)| d x$
  - I.e. integrate the absolute value (modulus) of the function
This will find the area
- between the curve $y = f (x)$ and the curve $y = g (x)$
- between $x = a$ and $x = b$
Because the absolute value changes any negative parts of $f (x) - g (x)$ into their positive equivalents
- you don't need to worry about which function is 'on top' in different parts of the area
  - You also don't need to worry about the order of the functions inside the absolute value
    - $|f (x) - g (x)| = |g (x) - f (x)|$

Worked Example

The shaded region in the diagram below is the region enclosed by the curves with equations $y = f (x)$ and $y = g (x)$ where

$f (x) = (x - 2) {(x - 3)}^{2}$

$g (x) = x^{2} - 5 x + 6$

Find the total area of the shaded region.

Answer:

Start by finding the $x$ -values of the points of intersection of the two curves

$\begin{array}{rcl} (x - 2) {(x - 3)}^{2} & = & x^{2} - 5 x + 6 \\ (x - 2) {(x - 3)}^{2} & = & (x - 2) (x - 3) \\ (x - 2) {(x - 3)}^{2} - (x - 2) (x - 3) & = & 0 \\ (x - 2) (x - 3) ((x - 3) - 1) & = & 0 \\ (x - 2) (x - 3) (x - 4) & = & 0 \end{array}$

$x = 2, x = 3, x = 4$

To work this out by hand we'd need to find the two areas separately, between $x = 2$ and $x = 3$ (where $y = f (x)$ is on top), and between $x = 3$ and $x = 4$ (where $y = g (x)$ is on top)

Instead we can work out the entire area between $x = 2$ and $x = 4$ with one integral using absolute value

$\begin{array}{rcl} Area & = & \int_{2}^{4} |f (x) - g (x)| d x \\ = & \int_{2}^{4} |(x - 2) {(x - 3)}^{2} - (x^{2} - 5 x + 6)| d x \end{array}$

That integral can be evaluated using your graphing calculator

$\begin{array}{rcl} \int_{2}^{4} |(x - 2) {(x - 3)}^{2} - (x^{2} - 5 x + 6)| d x & = & \frac{1}{2} = 0.5 \end{array}$

Total area = 0.5 units squared

Last updated: 26 August 2024

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Area Between Two CurvesNext:Volumes from Areas of Known Cross Sections

Multiple Areas (College Board AP® Calculus AB)

Study Guide

Using multiple definite integrals to find multiple areas

How do I find areas of enclosed regions partly above and partly below the x-axis using multiple integrals?

How do I find total areas between two curves using multiple integrals?

Worked Example

Using absolute value to find multiple areas

How do I find areas of regions partly above and partly below the x-axis using absolute value?

Examiner Tips and Tricks

Worked Example

How do I find total areas between two curves using absolute value?

Worked Example

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Roger B

Author: Dan Finlay