AP®MathsCollege BoardCalculus ABStudy GuidesUnit 8: Applications of IntegrationAreasArea Between a Curve & y-Axis

Area Between a Curve & y-Axis (College Board AP® Calculus AB)

Study Guide

Test yourself
Jamie Wood

Written by: Jamie Wood

Reviewed by: Dan Finlay

Area between a curve & y-axis

How do I find an area between a curve and the y-axis?

  • The value found when calculating a definite integral of a function x equals g open parentheses y close parentheses with respect to y between y equals a and y equals b, integral subscript a superscript b g open parentheses y close parentheses space italic d y

    • as long as g open parentheses y close parentheses greater or equal than 0 between those two y values

    • is equal to the area between the curve and the y-axis between y equals a and y equals b

  • Notice that a function in terms of y is being integrated with respect to y

    • This means if you are given a function in terms of x, i.e. y equals f open parentheses x close parentheses

    • You will need to rearrange it into a function in terms of y, i.e. x equals g open parentheses y close parentheses

Graph showing the area of region R under the curve y=f(x) between y=a and y=b, with the integral ∫ from a to b of x dy representing the area.

Worked Example

Find the area of the region enclosed by the curve with equation y equals 2 plus square root of x plus 4 end root, the y-axis, and the horizontal lines with equations y equals 4 and y equals 6. The graph of the curve is shown below.

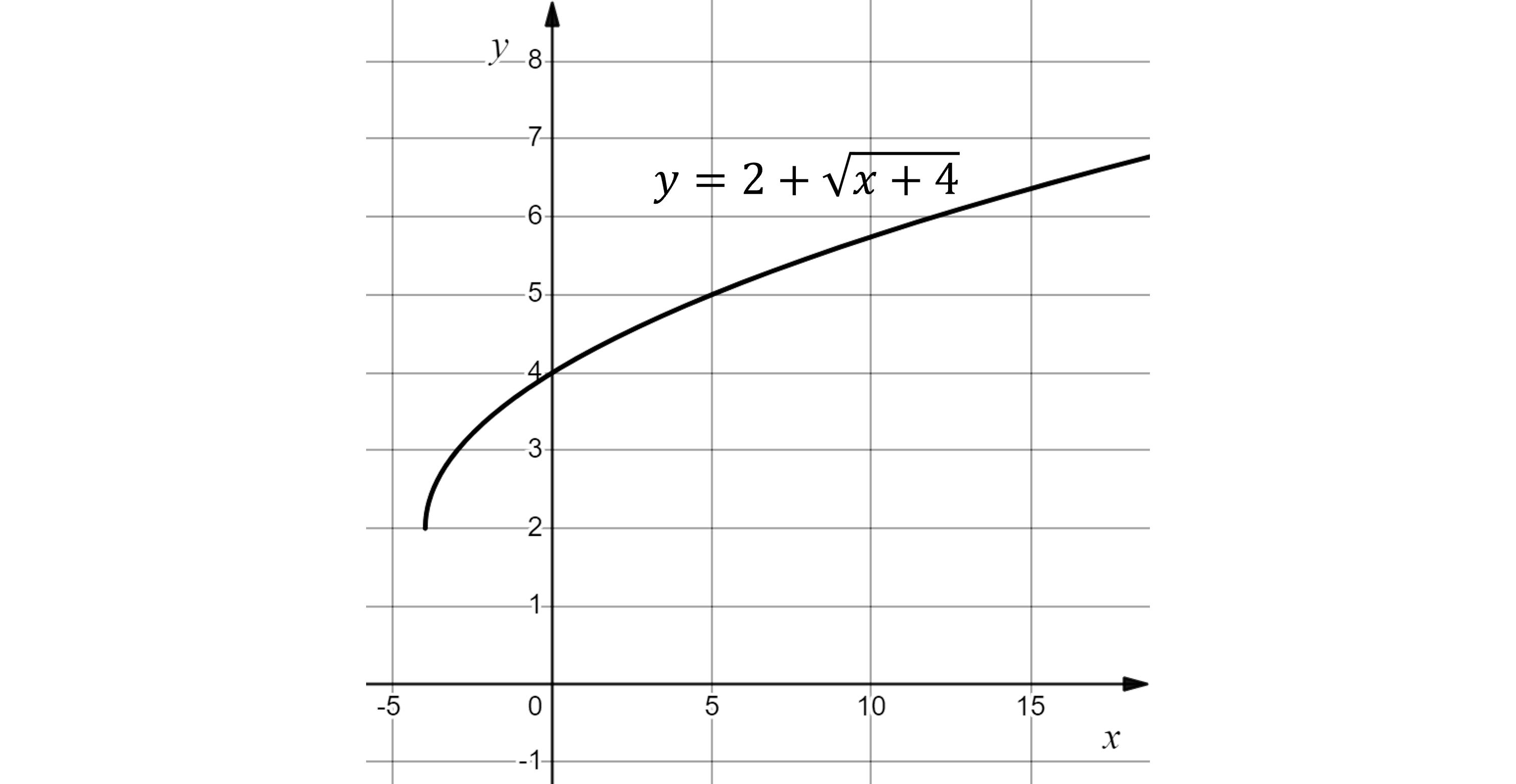
Graph of the function y = 2 + sqrt(x + 4) showing a curve starting from (-4, 2) and increasing gradually, plotted on a grid with x and y axes labeled.

Answer:

The diagram shows that the integral for the area between the curve, the y-axis, and y equals 6 and y equals 4 will be only positive (none of the area is to the left of the y-axis)

Rearrange the equation for y in terms of x, to make an equation for x in terms of y

table row y equals cell 2 plus square root of x plus 4 end root end cell row cell y minus 2 end cell equals cell square root of x plus 4 end root end cell row cell open parentheses y minus 2 close parentheses squared end cell equals cell x plus 4 end cell row cell open parentheses y minus 2 close parentheses squared minus 4 end cell equals x end table

Integrate this with respect to y between the y values of 4 and 6

table row cell integral subscript 4 superscript 6 open parentheses y minus 2 close parentheses squared minus 4 space italic d y space end cell equals cell space open square brackets 1 third open parentheses y minus 2 close parentheses cubed minus 4 y close square brackets subscript 4 superscript 6 end cell row blank equals cell space open parentheses 1 third open parentheses 6 minus 2 close parentheses cubed minus 4 open parentheses 6 close parentheses close parentheses minus open parentheses 1 third open parentheses 4 minus 2 close parentheses cubed minus 4 open parentheses 4 close parentheses close parentheses end cell row blank equals cell open parentheses negative 8 over 3 close parentheses minus open parentheses negative 40 over 3 close parentheses end cell row blank equals cell 32 over 3 end cell end table

32 over 3 units squared

What if I am not told the limits?

  •  If limits are not provided they will often be the y-axis intercepts

    • Set x equals 0 and solve the equation to find the y-axis intercepts first

    • Then integrate the function, written in terms of y, between the two y-axis intercepts

  • Remember that the x-axis (i.e. y equals 0) may also be one of the limits

When is the area integral negative?

  •  If the area lies to the left of the y-axis the value of the definite integral will be negative

    • However, an area cannot be negative

    • The area is equal to the modulus (absolute value) of the definite integral

  • If the area has some parts which are to the right of the y-axis, and some which are to the left of the y-axis

    • then see the method outlined in the 'Multiple Areas' study guide

Examiner Tips and Tricks

Always check whether you need to find the value of an integral, or an area.

  • When areas to the left of the y-axis are involved, these will be two different values.

Worked Example

Find the area of the region enclosed by the curve with equation x equals y squared minus 7 y plus 10 and the y-axis.

Answer:

Notice that in this question we are already given an equation for x in terms of y

We are not told any limits for this question, so we need to find where the y-intercepts are by solving for x equals 0

0 equals y squared minus 7 y plus 10 0 equals open parentheses y minus 2 close parentheses open parentheses y minus 5 close parentheses y equals 2 space or space y equals 5

The y-intercepts are at y equals 2 and y equals 5, this can be used to sketch a graph

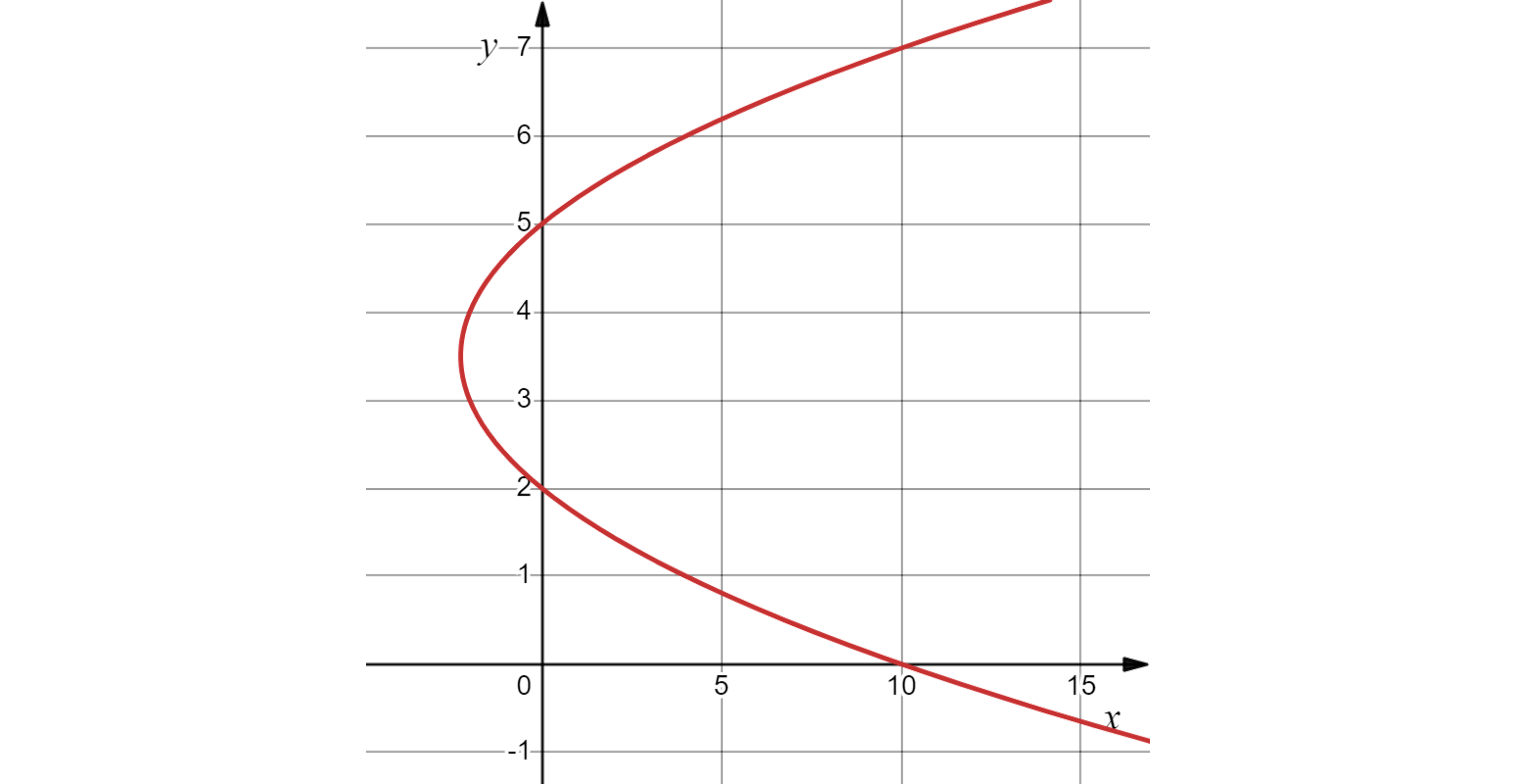
A red curve with y-intercepts of 2 and 5, and an x intercept of 10

It can now be seen that the area enclosed by the curve and the y-axis will be entirely on the left of the axis, and so the value of the integral will be negative

Remember to make this positive at the end, as it asks for an area

Integrate with respect to y between the y values of 2 and 5

table row cell integral subscript 2 superscript 5 y squared minus 7 y plus 10 space italic d y space end cell equals cell space open square brackets 1 third y cubed minus 7 over 2 y squared plus 10 y close square brackets subscript 2 superscript 5 end cell row blank equals cell open parentheses 1 third open parentheses 5 cubed close parentheses minus 7 over 2 open parentheses 5 squared close parentheses plus 10 open parentheses 5 close parentheses close parentheses minus open parentheses 1 third open parentheses 2 cubed close parentheses minus 7 over 2 open parentheses 2 squared close parentheses plus 10 open parentheses 2 close parentheses close parentheses end cell row blank equals cell 25 over 6 minus 26 over 3 end cell row blank equals cell negative 9 over 2 end cell end table

The question requires an area, rather than the value of the integral, so make this positive

9 over 2 units squared

Last updated:

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Area Between a Curve & x-AxisNext:Area Between Two Curves
    Author
    Reviewer
    Jamie Wood

    Author: Jamie Wood

    Expertise: Maths

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.