AP®MathsCollege BoardCalculus ABRevision NotesUnit 5: Analytical Applications of DifferentiationGraphs of Functions & Their DerivativesSecond Derivative Test for Local Extrema

Second Derivative Test for Local Extrema (College Board AP® Calculus AB)

Revision Note

Jamie Wood

Expertise

Maths

Second derivative test

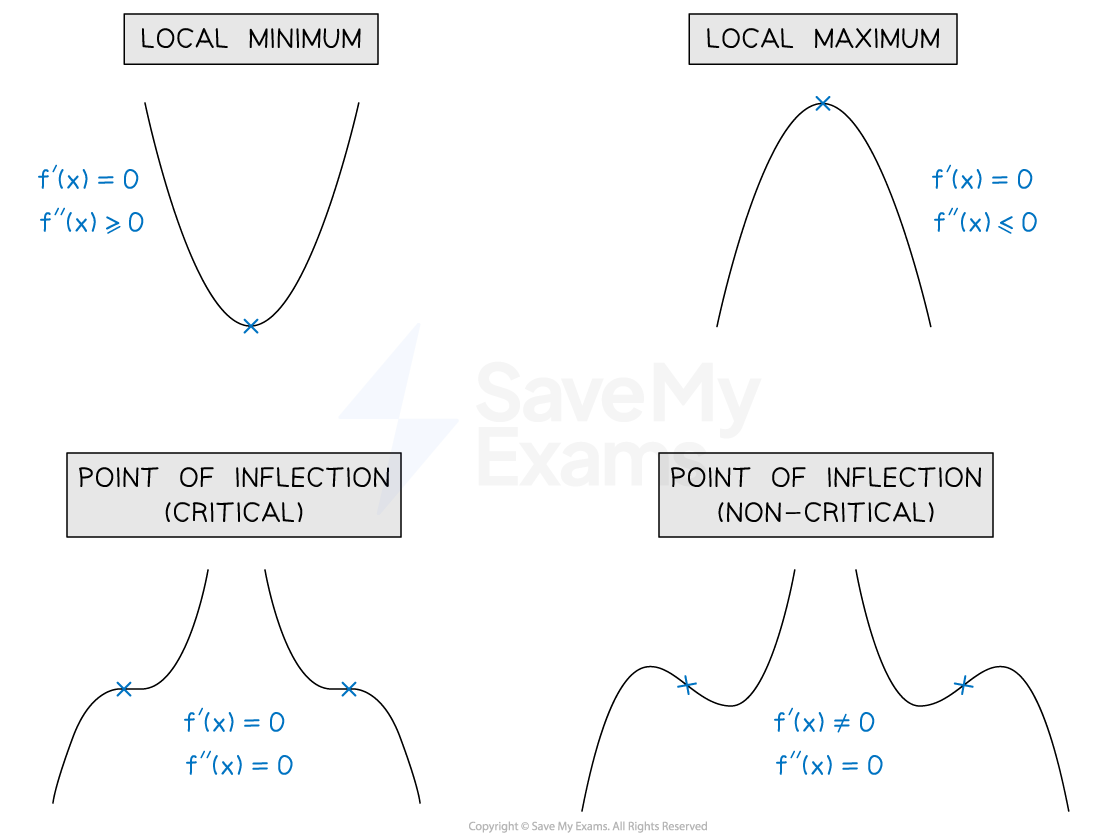
First and second derivatives at key points

  • To be able to classify key points on the graph of a function, it is important that you are confident with the properties of the first and second derivatives at these points

Type of point

First derivative

Second derivative

Local minimum

Zero

Positive or zero

Local maximum

Zero

Negative or zero

Point of inflection (critical)

Zero

Zero

Point of inflection (non-critical)

Non-zero

Zero

Diagram showing local minimum, local maximum, critical and non-critical points of inflection. Formulas included indicate first and second derivative conditions.

What is the second derivative test?

  • The information above means the second derivative can be used to determine if a critical point is a local minimum or maximum

  • The second derivative test states that:

    • If f to the power of apostrophe open parentheses a close parentheses equals 0 and f to the power of apostrophe apostrophe end exponent open parentheses a close parentheses greater than 0,

      • then f open parentheses x close parentheses has a local minimum at x equals a

    • If f to the power of apostrophe open parentheses a close parentheses equals 0 and f to the power of apostrophe apostrophe end exponent open parentheses a close parentheses less than 0,

      • then f open parentheses x close parentheses has a local maximum at x equals a

    • If f to the power of apostrophe open parentheses a close parentheses equals 0 and f to the power of apostrophe apostrophe end exponent open parentheses a close parentheses equals 0 then this test does not give any information

      • it could be any of a local minimum, local maximum, or point of inflection

Which points have a second derivative of zero?

  • All points of inflection have a second derivative of zero

  • However, not all points with a second derivative of zero are points of inflection

  • It is possible for local minimums or maximums to have a second derivative of zero

  • The second derivative test is only for determining if a critical point is a local minimum or maximum

  • If you find that f to the power of apostrophe apostrophe end exponent open parentheses x close parentheses equals 0 then you need to investigate further, by applying the first derivative test

    • Find the values of the first derivative:

      • at an x value slightly to the left of the critical point

      • at an x value slightly to the right of the critical point

    • If the first derivative changes (from left to right):

      • from positive to negative, it is a local maximum

      • from negative to positive, it is a local minimum

    • If the sign stays the same on both sides of the critical point, it is a point of inflection

Worked Example

Let the function f be defined by f open parentheses x close parentheses equals x cubed minus 3 x squared plus 3.

(a) Find the coordinates of any local extrema on the graph of f, and classify the nature of these extrema.

Answer:

Find the critical points by finding the first derivative and setting equal to zero

f to the power of apostrophe open parentheses x close parentheses equals 3 x squared minus 6 x

table row cell 3 x squared minus 6 x end cell equals 0 row cell x squared minus 2 x end cell equals 0 row cell x open parentheses x minus 2 close parentheses end cell equals 0 end table

x equals 2 or x equals 0

Find the y-coordinates at these points

f open parentheses 2 close parentheses equals negative 1

f open parentheses 0 close parentheses equals 3

Critical points at (2, -1) and (0, 3)

Classify these points by using the second derivative test

f to the power of apostrophe apostrophe end exponent open parentheses x close parentheses equals 6 x minus 6

Substitute the x value of each critical point into the second derivative

f to the power of apostrophe apostrophe end exponent open parentheses 2 close parentheses equals 6

Positive, so (2, -1) is a minimum

f to the power of apostrophe apostrophe end exponent open parentheses 0 close parentheses equals negative 6

Negative, so (0, 3) is a maximum

(2, -1) is a local minimum

(0, 3) is a local maximum

(b) Find the coordinates of the point of inflection on the graph of y equals f open parentheses x close parentheses. Justify how you know it is a point of inflection.

Answer:

Points of inflection have a second derivative of zero

Potential points of inflection can therefore be found by setting f apostrophe apostrophe open parentheses x close parentheses equals 0

f apostrophe apostrophe open parentheses x close parentheses equals 6 x minus 6

table row cell 6 x minus 6 end cell equals 0 row x equals 1 end table

Find the y-coordinate

f open parentheses 1 close parentheses equals 1

(1, 1)

So the point at (1, 1) could be a point of inflection

However, remember that minimums and maximums can also have a second derivative of zero

Check the first derivative at (1, 1) to see if it might be a minimum or maximum

f apostrophe open parentheses x close parentheses equals 3 x squared minus 6 x f apostrophe open parentheses 1 close parentheses equals negative 3

The point (1, 1) has a non-zero derivative, and a second derivative of zero

Therefore (1, 1) is a point of inflection

Worked Example

Use first and second derivatives to determine the nature of the critical point on the graph of g open parentheses x close parentheses equals 3 x to the power of 4 plus 2 x to the power of 6.

Answer:

Find the critical point first, by using f apostrophe open parentheses x close parentheses equals 0

f apostrophe open parentheses x close parentheses equals 12 x cubed plus 12 x to the power of 5

table row cell 12 x cubed plus 12 x to the power of 5 end cell equals 0 row cell 12 x cubed open parentheses 1 plus x squared close parentheses end cell equals 0 end table

x equals 0 is the only real solution

Find the y-coordinate

f open parentheses 0 close parentheses equals 0

The critical point is at (0, 0)

To determine the nature of the critical point, start by finding the second derivative at this point

f apostrophe apostrophe open parentheses x close parentheses equals 36 x squared plus 60 x to the power of 4

f apostrophe apostrophe open parentheses 0 close parentheses equals 0

First derivative is zero, and second derivative is zero

Therefore could be any of minimum, maximum, or point of inflection

Check the first derivative either side of the point to determine the nature of the point

f apostrophe open parentheses negative 1 close parentheses equals 12 open parentheses negative 1 close parentheses cubed plus 12 open parentheses negative 1 close parentheses to the power of 5 equals negative 24

f apostrophe open parentheses 1 close parentheses equals 12 open parentheses 1 close parentheses cubed plus 12 open parentheses 1 close parentheses to the power of 5 equals 24

The graph is changing from decreasing, to the left of (0, 0)
to increasing, to the right of (0, 0)

Therefore it is a minimum

The critical point at (0, 0) is a minimum point

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Next topic

    Did this page help you?

    Jamie Wood

    Author: Jamie Wood

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.