AP®MathsCollege BoardCalculus ABRevision NotesUnit 5: Analytical Applications of DifferentiationGraphs of Functions & Their DerivativesGraphs of f, f' & f''

Graphs of f, f' & f'' (College Board AP® Calculus AB)

Revision Note

Jamie Wood

Expertise

Maths

Graphs of f, f' & f''

How do I sketch the graph of a function?

  • You should already be familiar with the general shapes of the graphs of common functions, including

    • Linear functions

    • Quadratic Functions

    • Cubic and higher order polynomial functions

    • Trigonometric functions

    • Exponential and logarithmic functions

    • Reciprocals and reciprocal powers of x, e.g. 1 over x squared

  • You should also consider:

    • The domain of the function

      • The range is also useful, but you may need to use the candidates test for global extrema to find it

    • For which values of x is f open parentheses x close parentheses undefined?

      • There will be a vertical asymptote at these points

      • E.g. at x equals 0 on y equals 1 over x

    • The limit of the function as it tends to x equals plus-or-minus infinity

      • This can help you find a horizontal asymptote

      • E.g. at y equals 2 on y equals 1 over x plus 2

    • Is the function symmetrical in any way?

      • Is the function even, where f open parentheses negative x close parentheses equals f open parentheses x close parentheses

      • or odd, where f open parentheses negative x close parentheses equals negative f open parentheses x close parentheses ?

    • Does the graph repeat in some way, i.e. is it periodic?

      • i.e. f open parentheses x plus a close parentheses equals f open parentheses x close parentheses for some constant a

How can derivatives help me sketch the graph of a function?

  • Derivatives help identify key features and properties of the graph of a function

  • Recall the following properties of the first and second derivatives shown in the table below

Type of point

First derivative

Second derivative

Local minimum

Zero

Positive or zero

Local maximum

Zero

Negative or zero

Point of inflection (critical)

Zero

Zero

Point of inflection (non-critical)

Non-zero

Zero

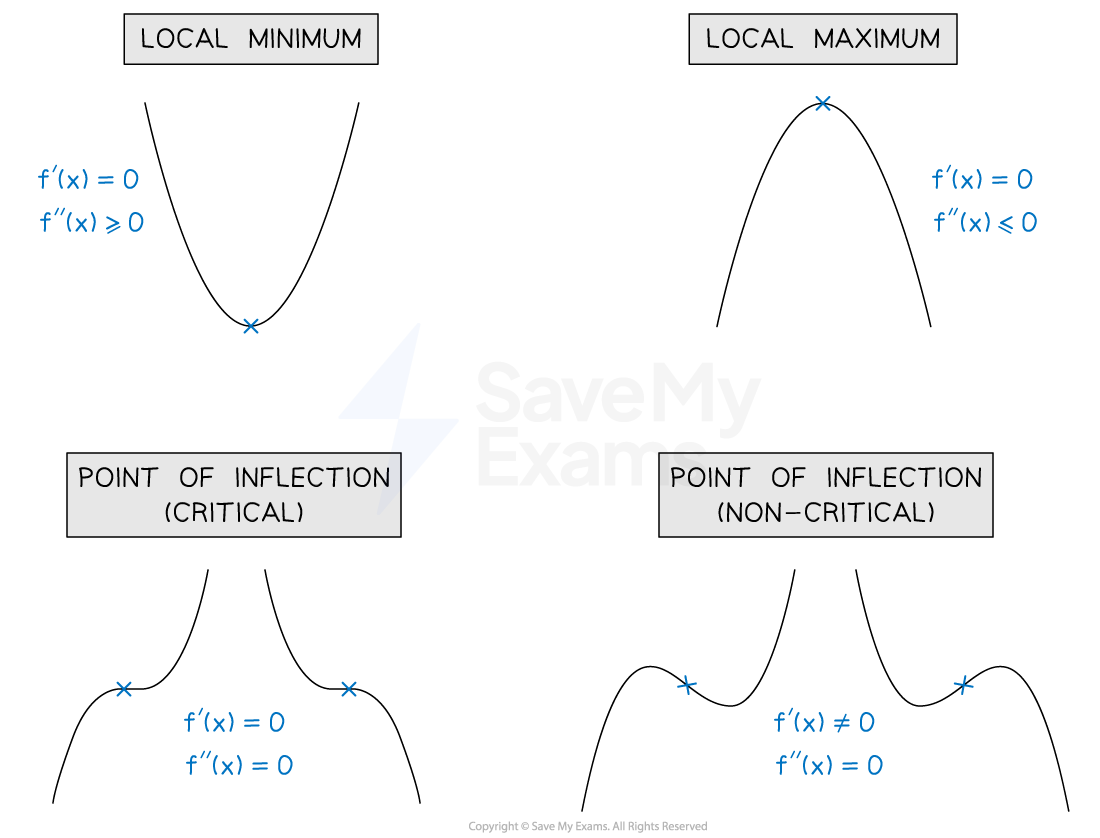
Diagram showing local minimum, local maximum, critical and non-critical points of inflection. Formulas included indicate first and second derivative conditions.

  • Knowing these facts and what they look like graphically (shown in the image above)

    • can help you sketch the graph of a function from its derivative

  • Remember that critical points also occur where the first derivative does not exist

    • At these points, the function itself must still be defined

    • A critical point where the first derivative does not exist is often where the tangent to the graph is vertical

      • E.g. at x equals 0 on the graph of y equals x to the power of 1 third end exponent

  • Also remember that at a point of inflection the second derivative changes sign (from positive to negative or vice versa)

    • It is not enough that f to the power of apostrophe apostrophe end exponent open parentheses x close parentheses equals 0

  • As well as key points, derivatives describe the behavior of a function within a region

    • Where f to the power of apostrophe open parentheses x close parentheses greater or equal than 0, the graph is increasing (from left to right)

    • Where f to the power of apostrophe open parentheses x close parentheses less or equal than 0, the graph is decreasing

    • Where f to the power of apostrophe apostrophe end exponent open parentheses x close parentheses greater or equal than 0, the graph is concave up, so will be u-shaped

    • Where f to the power of apostrophe apostrophe end exponent open parentheses x close parentheses less or equal than 0, the graph is concave down, so will be n-shaped

Worked Example

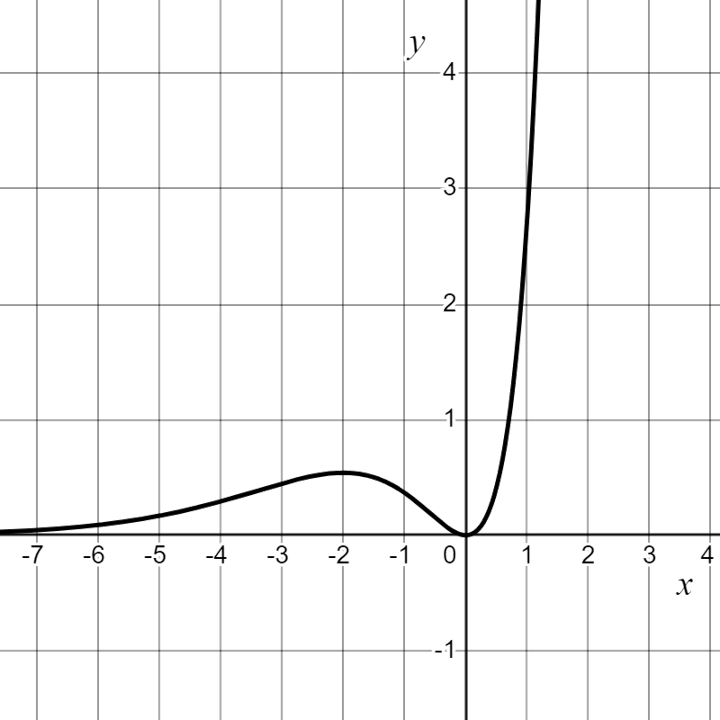
A curve with a local maximum at (-2, 0), a minimum at (0,0) and always above the x-axis.
Graph of f'

The graph of f to the power of apostrophe, the derivative of the function f, is shown above. Which of the following statements must be true?

i. f has a critical point at x equals 0.

ii. The graph of f has a point of inflection at x equals negative 2.

iii. The graph of f is concave up for negative 7 less than x less than 1.

iv. The function f is increasing for negative 7 less than x less than 1.

(A) i and ii only (B) i, ii, and iii only (C) i, ii, and iv only (D) i, ii, iii, and iv

Answer:

Let's look at each statement in turn to determine whether it is true or not

i. f has a critical point at x equals 0.

  • This is true as f to the power of apostrophe open parentheses x close parentheses equals 0 at x equals 0

  • therefore it is a critical point

ii. The graph of f has a point of inflection at x equals negative 2.

  • A point of inflection must have f to the power of apostrophe apostrophe end exponent open parentheses x close parentheses equals 0, so we must consider the slope of the graph of f to the power of apostrophe open parentheses x close parentheses

    • A tangent drawn at x equals negative 2 on f to the power of apostrophe open parentheses x close parentheses would be horizontal

    • therefore f to the power of apostrophe apostrophe end exponent open parentheses x close parentheses equals 0, so it could be a point of inflection

  • We still need to check whether the second derivative changes sign

    • To the left of x equals negative 2, the graph of f to the power of apostrophe is increasing, so f to the power of apostrophe apostrophe end exponent will be positive

    • To the right of x equals negative 2, the graph of f to the power of apostrophe is decreasing, so f to the power of apostrophe apostrophe end exponent will be negative

    • The sign of the second derivative changes at x equals negative 2, so it is a point of inflection

  • Therefore statement ii is true

iii. The graph of f is concave up for negative 7 less than x less than 1.

  • Concave up is when f to the power of apostrophe apostrophe end exponent open parentheses x close parentheses greater or equal than 0, so we need to consider whether or not the slope of f to the power of apostrophe open parentheses x close parentheses is always positive

  • The graph of f to the power of apostrophe open parentheses x close parentheses slopes downwards between x equals negative 2 and x equals 0

    • therefore f to the power of apostrophe is decreasing on that interval; f to the power of apostrophe apostrophe end exponent is negative

  • Therefore statement iii is false.

iv. The function f is increasing for negative 7 less than x less than 1.

  • For a function to be increasing, f to the power of apostrophe open parentheses x close parentheses must be non-negative

  • The graph of f to the power of apostrophe open parentheses x close parentheses is above or on the x-axis between -7 and 1, therefore f open parentheses x close parentheses is always increasing in this interval

  • Therefore statement iv is correct

So statements i, ii, and iv are true

Option (C)

Worked Example

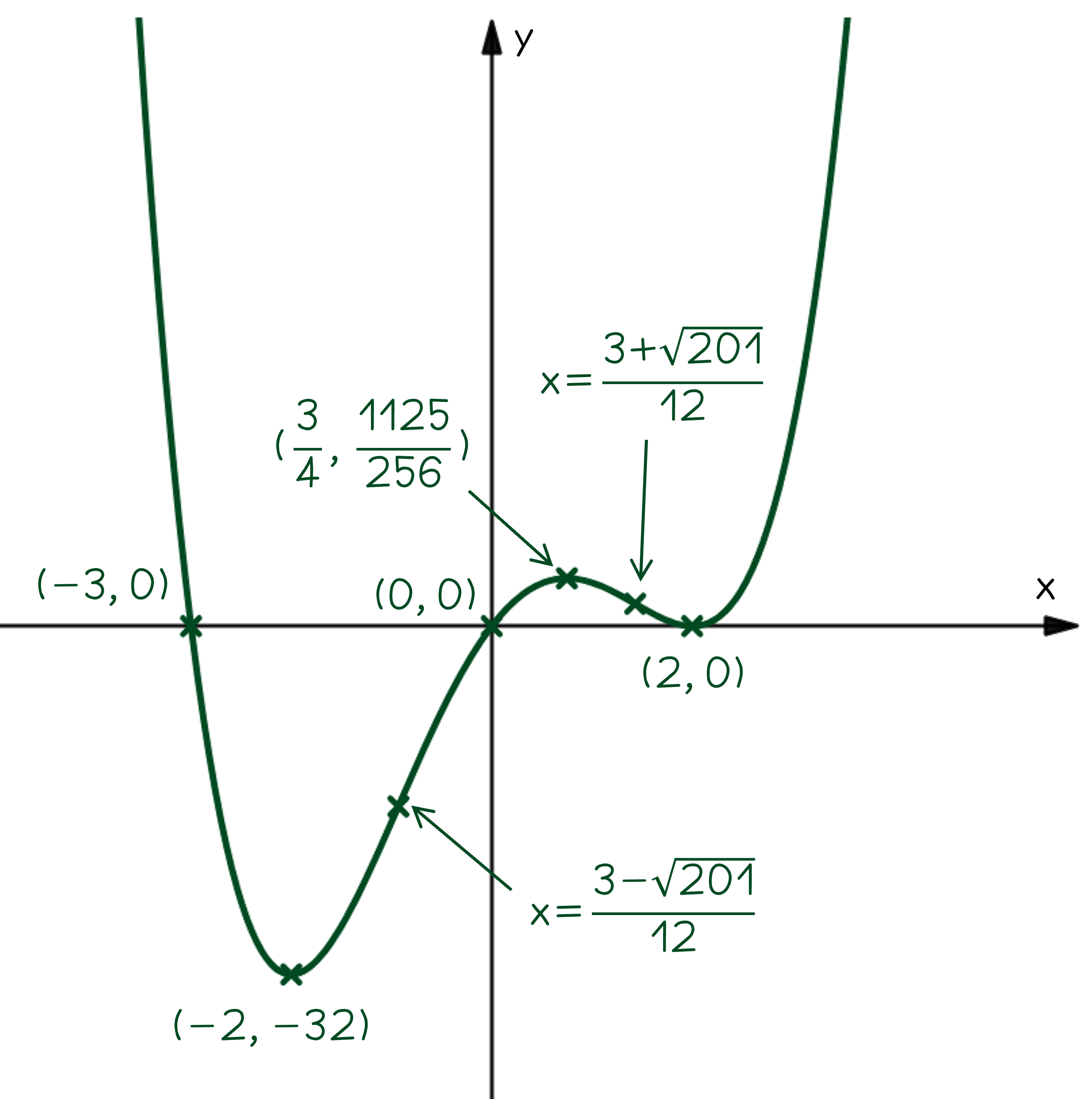
Let f be the function is defined by f open parentheses x close parentheses equals x open parentheses x minus 2 close parentheses squared open parentheses x plus 3 close parentheses.

Sketch the graph of y equals f open parentheses x close parentheses, labeling the coordinates of any axes intercepts and critical points, and stating the x values of any points of inflection.

Answer:

By inspecting the function, it can be seen that it is a positive quartic (i.e. highest power of x is 4)

This means overall it will have a w-shape, and will tend toward plus infinity as x tends to plus-or-minus infinity

The roots can also be found easily, by setting f open parentheses x close parentheses equals 0

x open parentheses x minus 2 close parentheses squared open parentheses x plus 3 close parentheses equals 0

Roots at x equals 0 and x equals negative 3, and a repeated root at x equals 2

Find any critical points where the first derivative is zero

Expand the equation first to make this easier

f open parentheses x close parentheses equals x to the power of 4 minus x cubed minus 8 x squared plus 12 x

f to the power of apostrophe open parentheses x close parentheses equals 4 x cubed minus 3 x squared minus 16 x plus 12 equals 0

You could solve this on your calculator, or by factorising

f to the power of apostrophe open parentheses x close parentheses equals open parentheses x minus 2 close parentheses open parentheses 4 x squared plus 5 x minus 6 close parentheses equals open parentheses x minus 2 close parentheses open parentheses 4 x minus 3 close parentheses open parentheses x plus 2 close parentheses equals 0

Critical points at x equals 2 comma space x equals 3 over 4 comma space x equals negative 2

Put these values into f open parentheses x close parentheses to find the y-coordinates

Critical points at (2, 0), (-2, -32), and open parentheses 3 over 4 comma fraction numerator space 1125 over denominator 256 end fraction close parentheses

This should be enough information to sketch the shape of the graph and its critical points, but it can be useful to check the concavity of each critical point

Use the second derivative to do this

f to the power of apostrophe apostrophe end exponent open parentheses x close parentheses equals 12 x squared minus 6 x minus 16

f to the power of apostrophe apostrophe end exponent open parentheses 2 close parentheses equals 20, positive, so u-shaped at x equals 2 (a minimum)

f to the power of apostrophe apostrophe end exponent open parentheses 3 over 4 close parentheses equals negative 55 over 4, negative, so n-shaped at x equals 3 over 4 (a maximum)

f to the power of apostrophe apostrophe end exponent open parentheses negative 2 close parentheses equals 44, positive, so u-shaped at x equals negative 2 (a minimum)

Check for any points of inflection, where the second derivative is equal to zero

All points of inflection have f apostrophe apostrophe open parentheses x close parentheses equals 0, but some critical points will also have f apostrophe apostrophe open parentheses x close parentheses equals 0. However we have already found all the critical points, so any remaining points where  f apostrophe apostrophe open parentheses x close parentheses equals 0 must be a point of inflection

f to the power of apostrophe apostrophe end exponent open parentheses x close parentheses equals 12 x squared minus 6 x minus 16 equals 0

x equals fraction numerator 3 plus-or-minus square root of 201 over denominator 12 end fraction

x equals 1.431453907... or x equals negative 0.9314539066...

These points of inflection are where the graph changes concavity, so will be in between the local minimums and maximums

Sketch the graph, labeling all the points as asked in the question

Graph of a positive quartic with 2 real roots, and one repeated root. Three stationary points are labelled, as well as two points of inflection

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Next topic

    Did this page help you?

    Jamie Wood

    Author: Jamie Wood

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.