Study GuidesExam QuestionsPast Papers
AP®MathsCollege BoardCalculus ABStudy GuidesUnit 5: Analytical Applications of DifferentiationGraphs of Functions & Their DerivativesCritical Points

Critical Points (College Board AP® Calculus AB)

Study Guide

Jamie Wood

Written by: Jamie Wood

Reviewed by: Dan Finlay

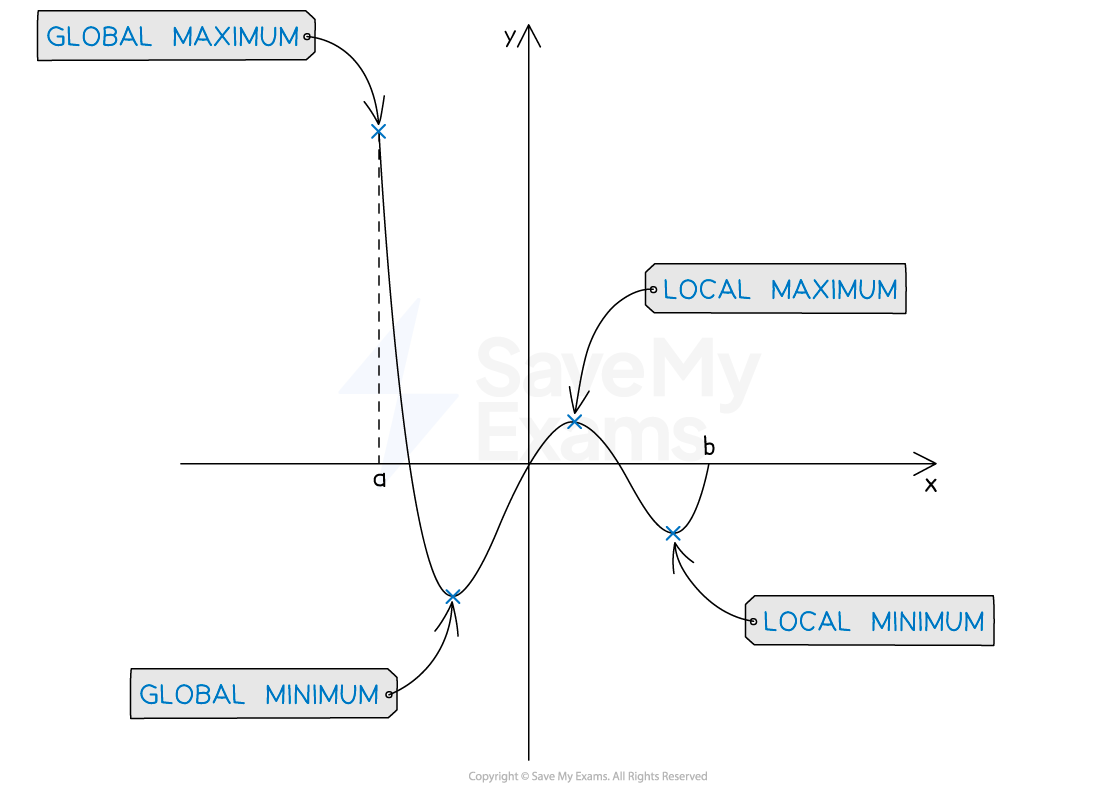
Local extrema versus global extrema

What is the difference between local and global extrema?

  • The term extremum (plural extrema) refers to maximum and minimum points on the graph of a function

  • An extremum can be either local (relative) or global

    • A global extremum is the maximum or minimum for the whole of a function's domain

    • A local or relative extremum is the maximum or minimum within a specific part of a function's domain

  • We can say that f open parentheses x close parentheses has a

    • global maximum at x equals c if

      • f open parentheses x close parentheses less or equal than f open parentheses c close parentheses for every x in the domain

    • local maximum at x equals c if

      • f open parentheses x close parentheses less or equal than f open parentheses c close parentheses for every x in some open interval around x equals c

    • global minimum at x equals c if

      • f open parentheses x close parentheses greater or equal than f open parentheses c close parentheses for every x in the domain

    • local minimum at x equals c if

      • f open parentheses x close parentheses greater or equal than f open parentheses c close parentheses for every x in some open interval around x equals c

  • Every global extremum will also be a local extremum

    • However not all local extrema are global extrema

Graph with x and y axes showing a curve with labeled points: "global maximum" at point a, "local maximum," "global minimum," and "local minimum" at point b.
The graph of a quartic function with domain between a and b. Note that global extrema can occur at the endpoints, or within an interval.

Critical points

What is a critical point?

  • A critical point is a point where the first derivative of a function is

    • equal to zero,

    • or does not exist

      • In the case where f to the power of apostrophe open parentheses a close parentheses does not exist, the function itself must still be defined at x equals a (i.e. f open parentheses a close parentheses must exist) in order for x equals a to be a critical point

      • E.g. y equals 1 over x does not have a critical point at x equals 0, but y equals x to the power of 2 over 3 end exponent does

  • All local extrema occur at critical points

    • However not all critical points are local extrema

What different types of critical points are there?

Local minimums and maximums

  • At local minimums and maximums, the derivative is most often equal to zero

    • I.e. for a function f, space f to the power of apostrophe open parentheses x close parentheses equals 0 at a local minimum or maximum

    • The tangent at these points is horizontal

    • There are some exceptions to this, for example where the function 'jumps' to a higher or lower value

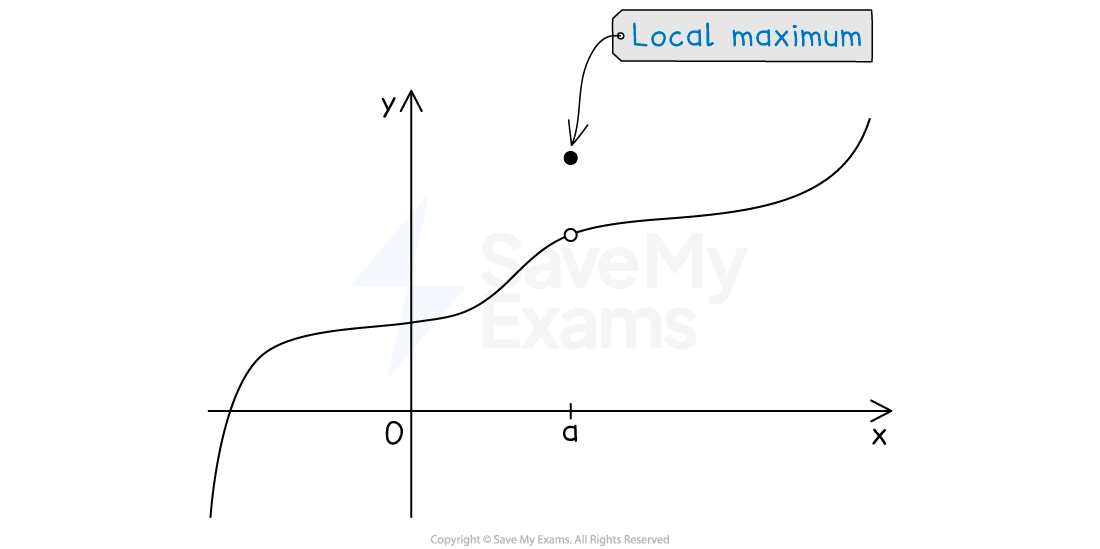
Graph of a curve with a discontinuity 'hole' at x=a (where a>0), and a single filled-in point above the curve also at x=a
An example of a local maximum point where the derivative is not equal to zero

  • Depending on the function, these can also be global extrema

    • E.g. The graph of y equals open parentheses x minus 2 close parentheses squared has a local minimum at (2,0), which is also a global minimum

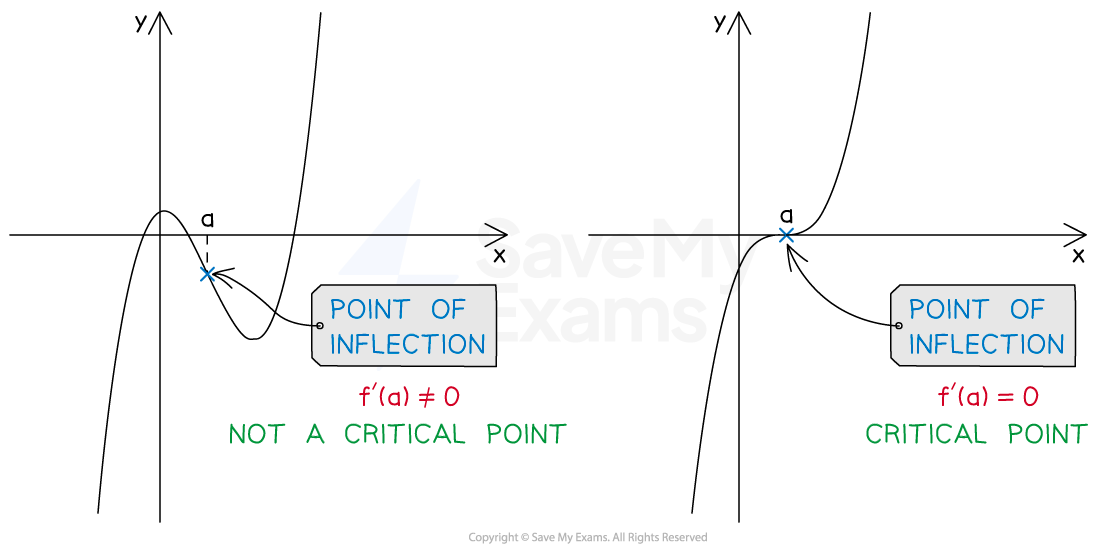
Points of inflection

  • A point of inflection is a point where a graph changes concavity

    • You can read more about concavity in the 'Concavity of Functions' study guide

  • Points of inflection are not local extrema

  • Only points of inflection where the first derivative is zero are critical points

    • It is possible for points of inflection to exist where the first derivative is not zero

  • A point of inflection with first derivative zero is sometimes referred to as a saddle point

    • E.g. y equals x cubed has a saddle point at x equals 0

Side-by-side graphs showing points of inflection: left graph with f'(a) ≠ 0 and not a critical point; right graph with f'(a) = 0 and a critical point.

Points where the derivative does not exist

  • As well as where the derivative is zero, a critical point occurs at points where the derivative does not exist

    • If the derivative does not exist at a point, the function itself must still be defined at that point to be a critical point

  • Consider the function f defined by f open parentheses x close parentheses equals 1 over x,

    • The function is undefined at x equals 0, so will not have a critical point at x equals 0

  • Consider the function g defined by g open parentheses x close parentheses equals cube root of x equals x to the power of 1 third end exponent

    • The function is defined at x equals 0 (it has a value of g open parentheses 0 close parentheses equals 0)

    • It has a first derivative of g to the power of apostrophe open parentheses x close parentheses equals 1 third x to the power of negative 2 over 3 end exponent equals fraction numerator 1 over denominator 3 cube root of x squared end root end fraction

    • The first derivative does not exist at x equals 0

    • So g has a critical point at x equals 0

  • The image below shows a similar example

Graph of f(x) = (x - 2)^(1/3) with annotations. f(x) defined at x=2, f(2)=0. Critical point at x=2. f'(x)=1/3(x-2)^(-2/3). f'(x) does not exist at x=2.

Worked Example

Find the coordinates of the critical point(s) on the graph of the function f defined by f open parentheses x close parentheses equals 4 x cubed minus 30 x squared plus 48 x plus 3.

Answer:

Find the points where the derivative is equal to zero

f to the power of apostrophe open parentheses x close parentheses equals 12 x squared minus 60 x plus 48

table row cell 12 x squared minus 60 x plus 48 end cell equals 0 row cell x squared minus 5 x plus 4 end cell equals 0 row cell open parentheses x minus 4 close parentheses open parentheses x minus 1 close parentheses end cell equals 0 end table

x equals 4 or x equals 1

f to the power of apostrophe open parentheses x close parentheses is exists for all x, so there are no other critical points (i.e. where the derivative does not exist)

Find the corresponding y values for these two critical points

f open parentheses 1 close parentheses equals 25 f open parentheses 4 close parentheses equals negative 29

A graph of the function is shown below

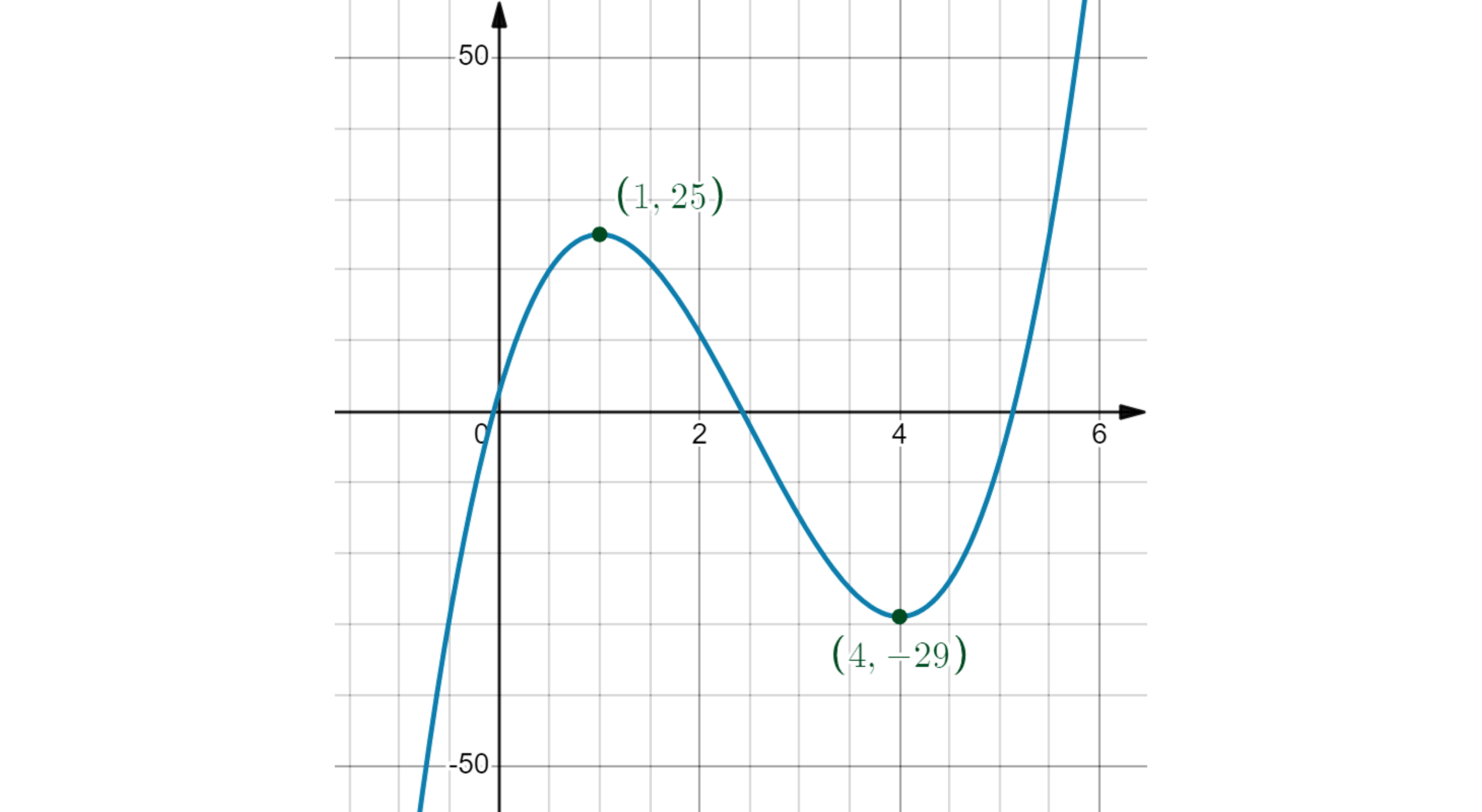
Graph of a cubic function with labeled points at (1, 25) and (4, -29). The curve increases, decreases, and then increases again with axes marked.

Critical points at (1, 25) and (4, -29)

Worked Example

Find the coordinates of the critical point(s) on the graph of the function g defined by g open parentheses x close parentheses equals open parentheses x minus 3 close parentheses to the power of 2 over 3 end exponent.

Answer:

Differentiate the function using the chain rule

g to the power of apostrophe open parentheses x close parentheses equals 2 over 3 open parentheses x minus 3 close parentheses to the power of negative 1 third end exponent equals fraction numerator 2 over denominator 3 open parentheses x minus 3 close parentheses to the power of 1 third end exponent end fraction

There are no points where the derivative is equal to zero

However the derivative will be undefined when x equals 3, as the denominator will be zero

The function is defined when x equals 3, as g open parentheses 3 close parentheses equals open parentheses 0 close parentheses to the power of 2 over 3 end exponent equals 0

However g to the power of apostrophe open parentheses 0 close parentheses is undefined, so there is a critical point at x equals 0

A graph of the function is shown below

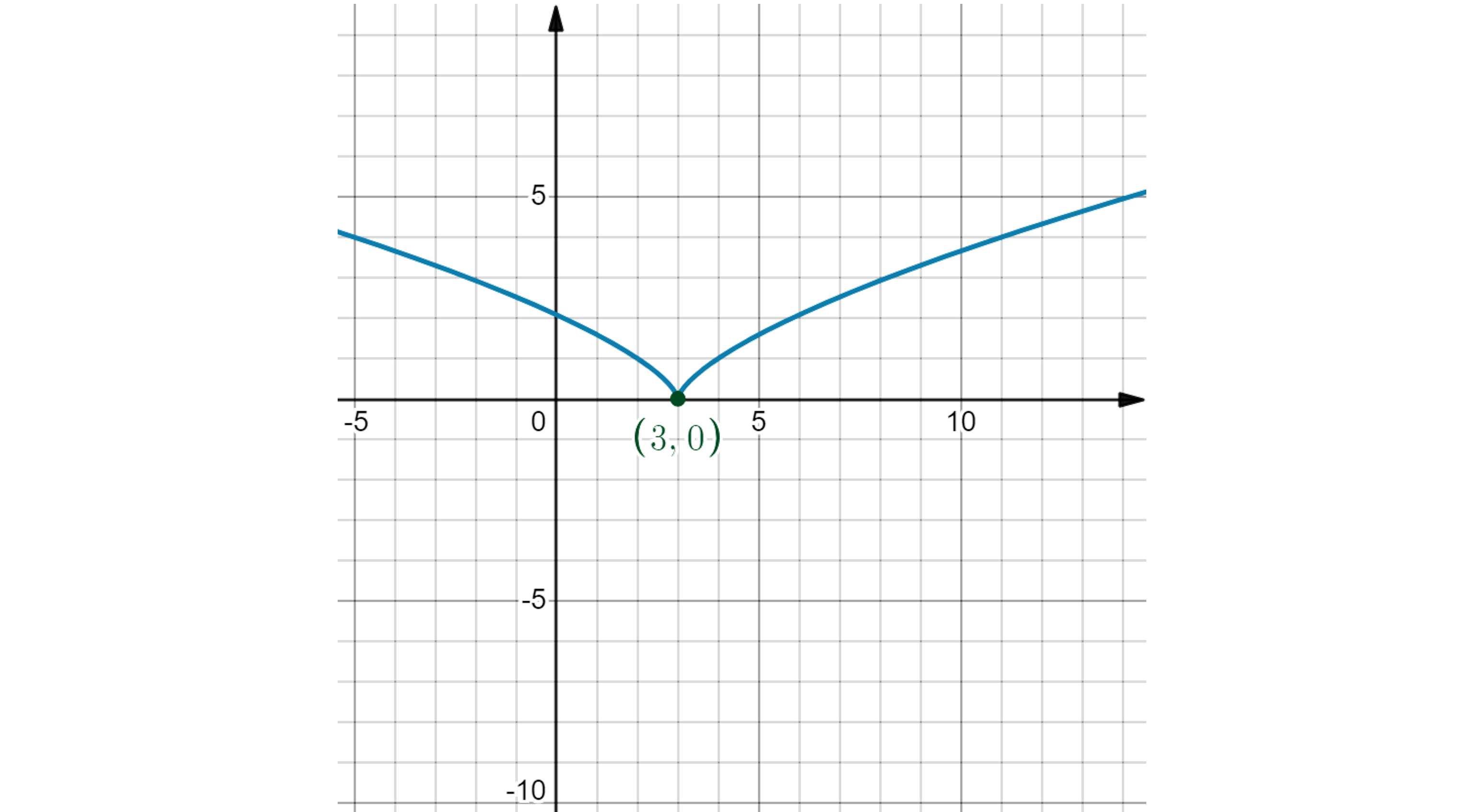
Graph of the quadratic function y = (x - 3)^(2/3) on a grid, with a cusp at (3, 0).

Critical point at (3, 0)

Last updated:

You've read 0 of your 5 free study guides this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Extreme Value TheoremNext:Increasing & Decreasing Functions
    Author
    Reviewer
    Jamie Wood

    Author: Jamie Wood

    Expertise: Maths

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.