AP®MathsCollege BoardCalculus ABStudy GuidesUnit 5: Analytical Applications of DifferentiationGraphs of Functions & Their DerivativesConcavity of Functions

Concavity of Functions (College Board AP® Calculus AB): Study Guide

Jamie Wood

Written by: Jamie Wood

Reviewed by: Dan Finlay

Updated on

College Board Calculus ABCollege Board Calculus BC

Concavity of functions

What is concavity?

  • Concavity is the way in which a curve bends, and is related to the second derivative of a function

  • A curve is:

    • Concave up ifspace f to the power of apostrophe apostrophe end exponent left parenthesis x right parenthesis greater or equal than 0 for all values ofspace x in an interval

      • f to the power of apostrophe open parentheses x close parentheses is increasing in this interval

    • Concave down ifspace f to the power of apostrophe apostrophe end exponent left parenthesis x right parenthesis less or equal than 0 for all values ofspace x in an interval

      • f to the power of apostrophe open parentheses x close parentheses is decreasing in this interval

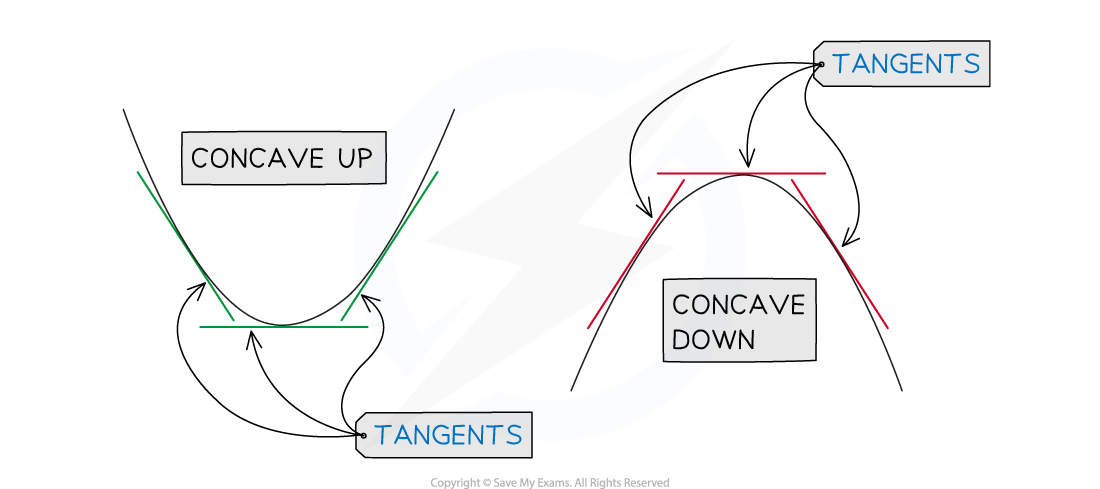
Diagram comparing concave up (left) and concave down (right) curves, highlighting tangent lines.

  • You can see from the diagram that;

    • At a local minimum a function is concave up

      • f to the power of apostrophe apostrophe end exponent open parentheses x close parentheses is positive

    • At a local maximum a function is concave down

      • f to the power of apostrophe apostrophe end exponent open parentheses x close parentheses is negative

  • A point where a graph changes in concavity,

    • from concave up to concave down or vice versa,

    • is called a point of inflection

  • Points of inflection will therefore always have a second derivative of zero

    • They can have any value for the first derivative

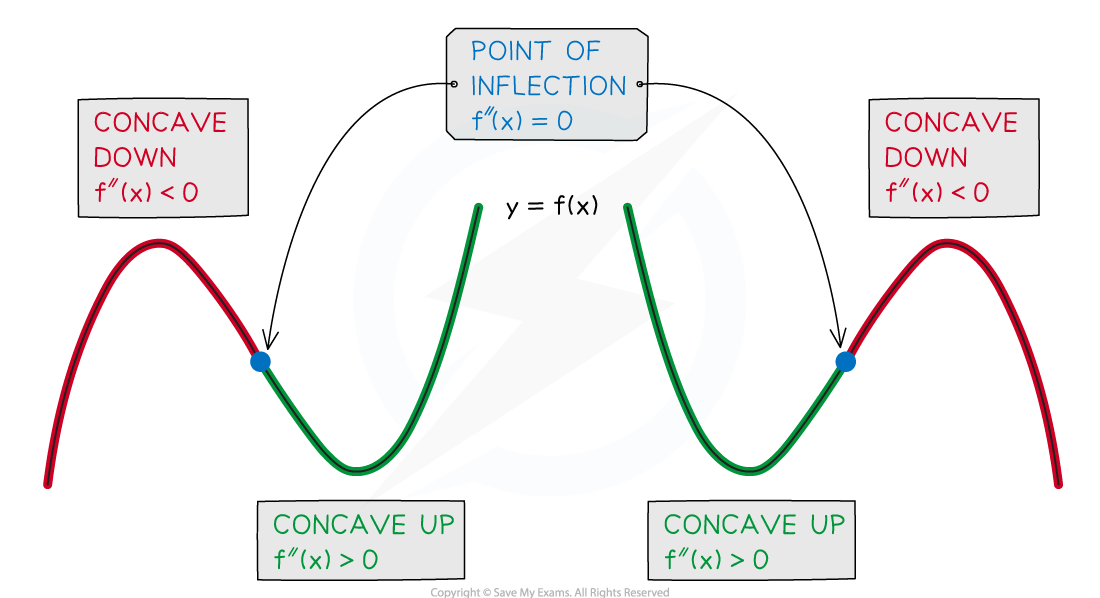
ib-aa-sl-5-2-5-point-of-inflection-diagram

  • Note that not every point with a second derivative of zero is a point of inflection

    • The concavity has to change as well

    • E.g. for f open parentheses x close parentheses equals x to the power of 4

      • f to the power of apostrophe apostrophe end exponent open parentheses 0 close parentheses equals 0

      • But x equals 0 is not a point of inflection

        • f to the power of apostrophe apostrophe end exponent open parentheses x close parentheses equals 12 x squared greater than 0 for all x not equal to 0

Examiner Tips and Tricks

In an exam an easy way to remember the difference is:

  • Concave down is the shape of (the mouth of) a sad smiley ☹️

    • They are feeling negative!

  • Concave up is the shape of (the mouth of) a happy smiley 🙂

    • They are feeling positive!

Worked Example

The function f is defined by

f open parentheses x close parentheses equals sin x comma space space space 0 less or equal than x less or equal than 2 pi

State the interval for which f is concave down.

Answer:

A function is concave down when f to the power of apostrophe apostrophe end exponent open parentheses x close parentheses is negative

table row cell f to the power of apostrophe open parentheses x close parentheses end cell equals cell cos x end cell row cell f to the power of apostrophe apostrophe end exponent open parentheses x close parentheses end cell equals cell negative sin x end cell end table

The following must then be solved in the given domain

negative sin x space less or equal than space 0 comma space space space 0 less or equal than x less or equal than 2 pi

The easiest way to solve this is with a graph of y equals negative sin x

Sketch the graph of y equals negative sin x for 0 less or equal than x less or equal than 2 pi and highlight where the graph is less than zero

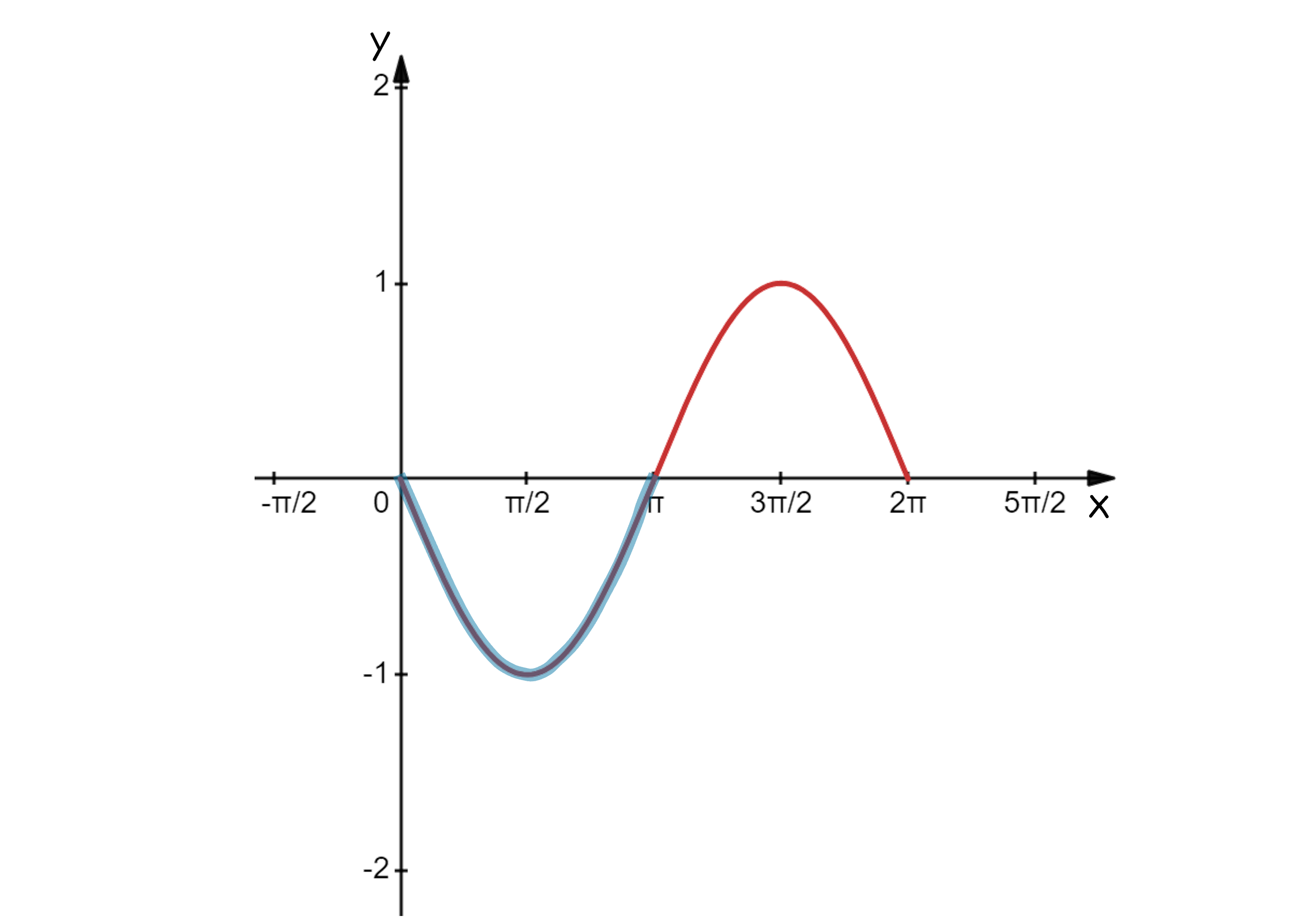
Graph of -sinx with 0 to pi highlighted (where it is below the x-axis)

The function is concave down on the interval where the second derivative is less than or equal to zero,

Concave down when 0 less or equal than x less or equal than pi

Alternatively you may have been able to find this region by inspecting the graph of y equals sin space x (the original function)

Concave down on [0, π]

You've read 1 of your 5 free study guides this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

  • I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

    Beth
    IGCSE Student

  • This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

    Fathima
    A Level Student
Test yourself

Did this page help you?

Previous:Candidates Test for Global ExtremaNext:Second Derivative Test for Local Extrema
Author
Reviewer
Jamie Wood

Author: Jamie Wood

Expertise: Maths Content Creator

Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

Dan Finlay

Reviewer: Dan Finlay

Expertise: Maths Subject Lead

Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

Download notes on Concavity of Functions