The Henderson-Hasselbalch Equation (College Board AP® Chemistry): Revision Note

The Henderson-Hasselbalch Equation

• The pH of a buffer solution can be calculated using:

  • The K_a of the weak acid

  • The equilibrium concentration of the weak acid and its conjugate base (salt)

• To determine the pH, the concentration of hydrogen ions is needed which can be found using the equilibrium expression

  • K_a = $\frac{\left[salt\right]\left[H^{+}\right]}{\left[acid\right]}$ which can be rearranged to [H⁺] = K_a x $\frac{\left[acid\right]}{\left[salt\right]}$

• To simplify the calculations, logarithms are used such that the expression becomes:

  • -log₁₀[H⁺] = -log₁₀ K_a x -log₁₀$\frac{\left[acid\right]}{\left[salt\right]}$

• Since -log₁₀ [H⁺] = pH, the expression can also be rewritten as:

  • pH = pKa + log₁₀ $\frac{\left[\mathrm{salt}\right]}{\left[\mathrm{acid}\right]}$

• This is known as the Henderson-Hasselbalch equation

• For weak bases a similar derivation occurs:

  • pOH = pK_b + log₁₀ $\frac{\left[\mathrm{salt}\right]}{\left[\mathrm{base}\right]}$

What happens when acids and bases are added to a buffer solution?

Consider ethanoic acid and sodium enthanoate as a buffer system

CH₃COOH (aq) $\rightleftharpoons$ CH₃COO^– (aq) + H⁺ (aq)

• When H⁺ ions are added to an acidic buffer:

  • The equilibrium position shifts to the left as H⁺ ions react with CH₃COO^- ions to form more CH₃COOH until equilibrium is re-established

  • As there is a large reserve supply of CH₃COO^- the concentration of CH₃COO^- in solution doesn’t change much as it reacts with the added H⁺ ions

  • As there is a large reserve supply of CH₃COOH the concentration of CH₃COOH in solution doesn’t change much as CH₃COOH is formed from the reaction of CH₃COO^- with H⁺

• The ratio of $\frac{\left[\mathrm{salt}\right]}{\left[\mathrm{acid}\right]}$ remains reasonably constant and thus does not significantly change the solution pH

When hydrogen ions are added to the solution the pH of the solution would decrease. However, the ethanoate ions in the buffer solution react with the hydrogen ions to prevent this and keep the pH constant

• When OH^- ions are added to an acidic buffer:

  • The OH^- reacts with H⁺ to form water

OH^- (aq) + H⁺  (aq) → H₂O (l)

• The H⁺ concentration decreases

• The equilibrium position shifts to the right and more CH₃COOH molecules ionise to form more H⁺and CH₃COO^- until equilibrium is re-established

CH₃COOH (aq) → H⁺ (aq) + CH₃COO^- (aq)

• As there is a large reserve supply of CH₃COOH the concentration of CH₃COOH in solution doesn’t change much when CH₃COOH dissociates to form more H⁺ ions

• As there is a large reserve supply of CH₃COO^- the concentration of CH₃COO^- in solution doesn’t change much

• The ratio of $\frac{\left[\mathrm{salt}\right]}{\left[\mathrm{acid}\right]}$remains reasonably constant and thus does not significantly change the solution pH

When hydroxide ions are added to the solution, the hydrogen ions react with them to form water. The decrease in hydrogen ions would mean that the pH would increase however the equilibrium moves to the right to replace the removed hydrogen ions and keep the pH constant

Changing concentrations of HA and A^-

• The Hendersen-Hasselback equation can be used to demonstrate the implications on the pH of the buffer solution is the concentration on HA and A^– are changed

  • pH = pK_a + log₁₀$\frac{\left[\mathrm{salt}\right]}{\left[\mathrm{acid}\right]}$

• For example,

  • A common buffer contains CH₃COOH and CH₃COO^–

  • If the ratio [CH₃COOH] and [CH₃COO^–]  change the pH of the buffer solution will change

Ratio of [CH₃COOH] and [CH₃COO^–] in a buffer

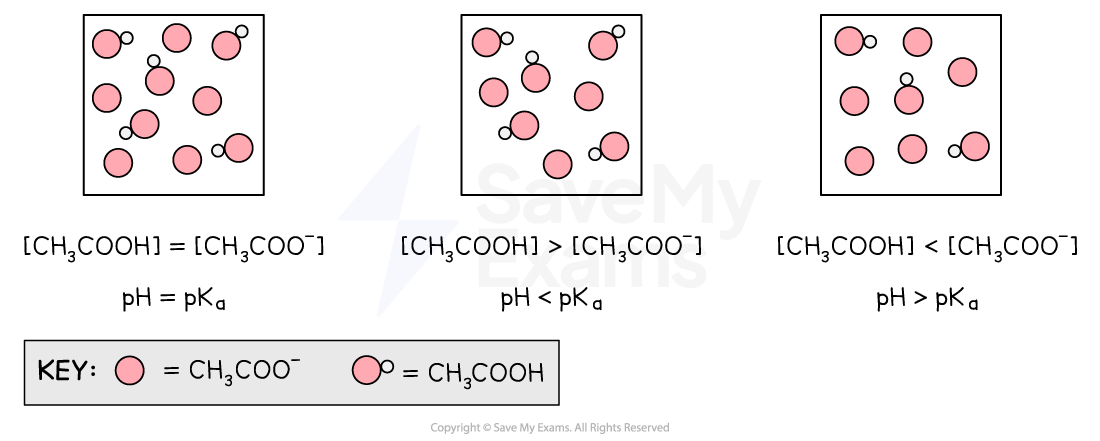
 The pH of a buffer will vary depending on the concentration of the acid and salt

• pH = pK_a + log₁₀ $\frac{\left[{\mathrm{CH}}_3{\mathrm{COO}}^{-}\right]}{\left[{\mathrm{CH}}_3\mathrm{COOH}\right]}$

• If [CH₃COOH] and [CH₃COO^–] are equal:
  

  • The pH will = pK_a

• If [CH₃COOH] is greater than (>) [CH₃COO^–]

  • The pH will be greater than pK_a

• If [CH₃COOH] is less than (<) [CH₃COO^–]

  • The pH will be less than pK_a