AP®ChemistryCollege BoardStudy GuidesUnit 7: EquilibriumSolubility EquilibriaSolubility-Product Constant

Solubility-Product Constant (College Board AP® Chemistry)

Study Guide

Test yourself
Philippa Platt

Written by: Philippa Platt

Reviewed by: Stewart Hird

Solubility-Product Constant, Ksp

  • Solubility is defined as the number of grams or moles of compound needed to saturate 100 mL of water, or it can also be defined in terms of 1 litre of water, at a given temperature

    • For example, sodium chloride (NaCl) is considered to be a soluble salt as a saturated solution contains 36 g of NaCl per 100 mL of water

    • Lead chloride (PbCl2) on the other hand is an insoluble salt as a saturated solution only contains 0.99 g of PbCl2 per 100 mL of water

Solubility product

  • The solubility product (Ksp) is:

    • The product of the concentrations of each ion in a saturated solution of a relatively soluble salt

    • At 298 K

    • Raised to the power of their relative concentrations

C (s) ⇌ aAx+ (aq) + bBy- (aq)

Ksp = [Ax+ (aq)]a [By- (aq)]b

  • When an undissolved ionic compound is in contact with a saturated solution of its ions, an equilibrium is established

  • The ions move from the solid to the saturated solution at the same rate as they move from the solution to the solid

    • For example, the undissolved magnesium chloride (MgCl2) is in equilibrium with a saturated solution of its ions

MgCl2 (s) ⇌ Mg2+ (aq) + 2Cl- (aq)

Ions in a saturated solution

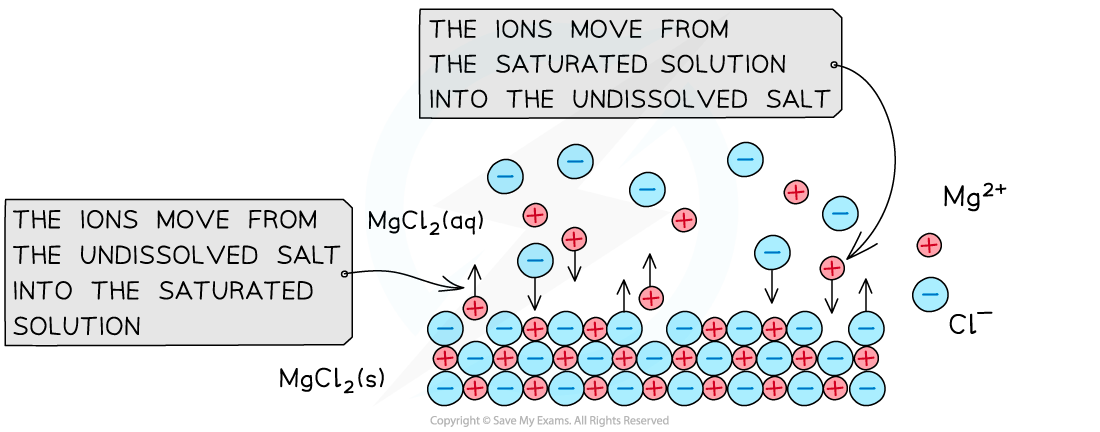
Equilibria - Equilibrium between Ionic Compound and Saturated Solution, downloadable AS & A Level Chemistry revision notes

When the undissolved MgCl2 salt comes in contact with its ions in a saturated solution, an equilibrium between the salt and ions is established

  • The solubility product for this equilibrium is:

Ksp = [Mg2+ (aq)] [Cl- (aq)]2

  • The Ksp is only useful for sparingly soluble salts

  • The smaller the value of Ksp, the lower the solubility of the salt

Solubility-Product Constant Calculations

  • Calculations involving the solubility product (Ksp) are solved as other equilibrium problems

Worked Example

Calculating the solubility product of a compound from its solubility

Calculate the solubility product of a saturated solution of lead(II) bromide, PbBr2, with a solubility of 1.39 x 10-3 mol dm-3.

Answer:

  • Step 1: Write down the equilibrium equation and expression:

PbBr2 (s) ⇌ Pb2+ (aq) + 2Br- (aq)

Ksp = [Pb2+(aq)] [Br- (aq)]2

  • Step 2: Set up an equilibrium table:

Reaction

PbBr2 (s)

⇌

Pb2+ (aq)

+

2Br- (aq)

Initial Conc.

Solid

 

0 M

 

0 M

Change

–x dissolves 

 

+ x

 

+ 2x

Equilibrium

solid remaining

 

+ x

 

+ 2x

  • Step 3: Calculate the ion concentrations in the solution:

    • [PbBr2(s)] = 1.39 x 10-3 mol dm-3

    • The ratio of PbBr2 to Pb2+ is 1:1

      • [Pb2+(aq)] = [PbBr2(s)] = 1.39 x 10-3 mol dm-3

    • The ratio of PbBr2 to Br- is 1:2

      • [Br-(aq)] = 2 x [PbBr2(s)] = 2 x 1.39 x 10-3 mol dm-3 = 2.78 x 10-3 mol dm-3

  • Step 4: Substitute the values into the expression to find the solubility product:

    • Ksp = (1.39 x 10-3) x (2.78 x 10-3)2

    • Ksp = 1.07 x 10-8

  • Therefore, the solubility product is 1.07 x 10-8

Worked Example

Calculating the solubility of a compound from its solubility product

Calculate the solubility of a saturated solution of copper(II) oxide, CuO, with a solubility product of 5.9 x 10-36.

Answer:

  • Step 1: Write down the equilibrium equation and expression:

CuO (s) ⇌ Cu2+ (aq) + O2- (aq)

Ksp = [Cu2+ (aq)] [O2- (aq)]

  • Step 2: Set up an equilibrium table:

Reaction

CuO (s)

⇌

Cu2+ (aq)

+

O2- (aq)

Initial Conc.

Solid

 

0 M

 

0 M

Change

–x dissolves 

 

+ x

 

+ x

Equilibrium

solid remaining

 

+ x

 

+ x

  • Step 3: Simplify the equilibrium expression:

    • The ratio of Cu2+ to O2- is 1:1

    • [Cu2+(aq)] = [O2-(aq)] so the expression can be simplified to:

      • Ksp = [Cu2+ (aq)]2

  • Step 4: Substitute the value of Ksp into the expression to find the concentration:

    • 5.9 x 10-36 = [Cu2+ (aq)]2

    • [Cu2+ (aq)] = begin mathsize 14px style square root of bold 5 bold. bold 9 bold cross times bold 10 to the power of bold minus bold 36 end exponent end root end style

    • [Cu2+ (aq)] = 2.4 x 10-18 

  • Since [CuO (s)] = [Cu2+ (aq)], the solubility of copper oxide is 2.4 x 10-18 

Examiner Tips and Tricks

Remember that the solubility product is only applicable to very slightly soluble salts and cannot be used for soluble salts such as:

  • Group 1 element salts

  • All nitrate salts

  • All ammonium salts

  • Many sulfate salts

  • Many halide salts (except for lead(II) halides and silver halides)

Applying Solubility Rules to Ksp

  • A salt is soluble if at least 0.1 mol of the salt will dissolve in 1 L of water

  • Saturated solutions of insoluble salts have concentration that are less than 0.1 molar, however, most insoluble salts do dissolve to a small extent 

  • As we have seen before with equilibria, we can relate Ksp to the reaction quotient, Q

  • This will help us predict if a precipitation reaction will produce more or less precipitate to adjust to equilibrium

  • If Q > K the reaction will favour the left hand side (backward reaction) and form more reactant

    • Solubility decreases as precipitate forms

  • If Q < K the reaction will favour the right hand side (forward reaction) and form more product

    • Solubility increases as more ions dissolve

  • And if Q = K, the reaction is at equilibrium

Worked Example

A 1.70 x 10-3 M solution of calcium nitrate is mixed with an equal volume of 1.50 x 10-3 potassium sulfate.

Predict whether calcium sulfate (Ksp = 2.00 x 10-5) will precipitate. 

Answer:

Step 1: Write the equation:

  • Ca(NO3)2 + K2SO4 → CaSO4 + 2KNO3

Step 2: Determine the concentration of the calcium and sulfate ions 

  • You must half the concentrations of the solutions as you are doubling the volume

    • The question says you are adding equal volumes of both solutions

  • [Ca2+ (aq)] = fraction numerator 1.70 space cross times space 10 to the power of negative 3 end exponent over denominator 2 end fraction = 8.50 x 10-4 M

    [SO42- (aq)] = fraction numerator 1.50 space cross times 10 to the power of negative 3 end exponent over denominator 2 end fraction = 7.50 x 10-4 M

Step 3: Calculate Q

  • [Ca2+ (aq)] x [SO42- (aq)] = 8.50 x 10-4 x 7.50 x 10-4 = 6.38 x 10-7 

Step 4: Compare to Ksp

  • Therefore, the will be no precipitation as Q is less than Ksp (of calcium sulfate)

Last updated:

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Reaction Quotient & Le Châtelier’s PrincipleNext:Common-Ion Effect
    Author
    Reviewer
    Philippa Platt

    Author: Philippa Platt

    Expertise: Chemistry

    Philippa has worked as a GCSE and A level chemistry teacher and tutor for over thirteen years. She studied chemistry and sport science at Loughborough University graduating in 2007 having also completed her PGCE in science. Throughout her time as a teacher she was incharge of a boarding house for five years and coached many teams in a variety of sports. When not producing resources with the chemistry team, Philippa enjoys being active outside with her young family and is a very keen gardener

    Stewart Hird

    Author: Stewart Hird

    Expertise: Chemistry Lead

    Stewart has been an enthusiastic GCSE, IGCSE, A Level and IB teacher for more than 30 years in the UK as well as overseas, and has also been an examiner for IB and A Level. As a long-standing Head of Science, Stewart brings a wealth of experience to creating Topic Questions and revision materials for Save My Exams. Stewart specialises in Chemistry, but has also taught Physics and Environmental Systems and Societies.