AP®ChemistryCollege BoardStudy GuidesUnit 7: EquilibriumSolubility EquilibriaCommon-Ion Effect

Common-Ion Effect (College Board AP® Chemistry)

Study Guide

Test yourself
Philippa Platt

Written by: Philippa Platt

Reviewed by: Stewart Hird

Common-Ion Effect

  • A saturated solution is a solution that contains the maximum amount of dissolved salt

  • If a second compound, which has an ion in common with the dissolved salt, is added to the saturated solution, the solubility of the salt reduces and a solid precipitate will be formed

  • This is also known as the common ion effect

  • For example, if a solution of potassium chloride (KCl) is added to a saturated solution of silver chloride (AgCl) a precipitate of silver chloride will be formed

    • The chloride ion is the common ion

  • The solubility product can be used to predict whether a precipitate will form or not

    • A precipitate will form if the product of the ion concentrations is greater than the solubility product (Ksp)

Common ion effect in silver chloride

  • When a KCl solution is added to a saturated solution of AgCl, an AgCl precipitate forms

  • In a saturated AgCl solution, the silver chloride is in equilibrium with its ions

AgCl (s) ⇌ Ag+ (aq) + Cl- (aq)

  • When a solution of potassium chloride is added:

    • Both KCl and AgCl have the common Cl- ion

    • There is an increased Cl- concentration so the equilibrium position shifts to the left

    • The increase in Cl- concentration also means that [Ag+ (aq)] [Cl-(aq)] is greater than the Ksp for AgCl

    • As a result, the AgCl is precipitated

The common ion effect with KCl (aq) and AgCl (aq)

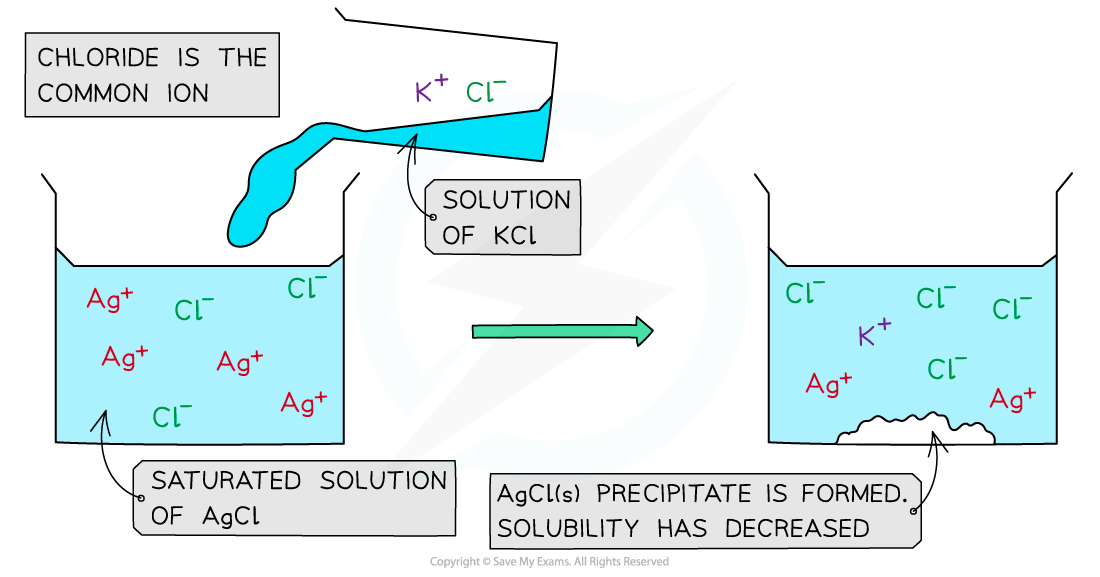
Equilibria - Common Ion Effect, downloadable AS & A Level Chemistry revision notes

The addition of potassium chloride to a saturated solution of silver chloride results in the precipitate of silver chloride

Worked Example

Calculations using the Ksp values and the concentration of the common ion

Predict whether a precipitate of CaSO4 will form if a saturated solution of 1.0 x 10-3 M CaSO4 is mixed with an equal volume of 1.0 x 10-3 M Na2SO4.

Ksp CaSO4 = 2.0 x 10-5 

Answer:

  • Step 1: Determine the equilibrium reaction of CaSO4:

    • CaSO4 (s) ⇌ Ca2+ (aq) + SO42- (aq)

  • Step 2: Write down the equilibrium expression for Ksp:

    • Ksp = [Ca2+ (aq)] [SO42- (aq)]

CaSO4 (s)

rightwards harpoon over leftwards harpoon

Ca2+ (aq)

+

SO42- (aq)

x

 

0

 

0

-x

 

+ x

 

+ x

 

 

5.0 x 10-4

 

x + 1 x 10-3

  • Step 3: Determine the concentrations of the ions:

  • There are equal volumes of each solution

  • This means that the total solution was diluted by a factor of 2

  • The new concentration of the Ca2+ ion is halved:

    • [Ca2+] =  begin mathsize 14px style fraction numerator 1.0 cross times 10 to the power of negative sign 3 end exponent over denominator 2 end fraction end style

    • [Ca2+] = 5.0 x 10-4 M

  • The sulfate ion concentration remains the same as it is a common ion and its concentration is the same in both solutions

  • Step 4: Substitute the values into the expression:

    • Product of the ion concentrations = [Ca2+ (aq)] x [SO42- (aq)]

    • Product of the ion concentrations = (5.0 x 10-4) x (1.0 x 10-3)

    • Product of the ion concentrations = 5.0 x 10-7 M

  • Step 5: Determine if a precipitate will form:

    • As Q (5.0 x 10-7 M) is smaller than the Ksp value (2.0 x 10-5 M), the CaSO4 precipitate will not be formed

Worked Example

The Ksp for lead chloride, PCl2 is 1.7 x 10-5 at 25 °C.

Calculate the molar solubility of PCl2 at 25 °C which is in a solution of 0.10 NaCl.

Answer:

  • Step 1: Write equation and expression

    • PbCl2 (s) rightwards harpoon over leftwards harpoon Pb2+ (aq) + 2Cl– (aq)

    • Ksp = [Pb2+ (aq)][Cl– (aq)]2

  • Step 2: Calculate concentrations of ions

PbCl2 (s)

rightwards harpoon over leftwards harpoon

Pb2+ (aq)

+

2Cl– (aq)

x

 

0

 

0

-x

 

+ x

 

+ 2x

 

 

5.0 x 10-4

 

2x + 0.10

  • Step 3: Place values into expression

    • Ksp = [Pb2+ (aq)][Cl– (aq)]2 

    • 1.7 x 10-5 = (x)(2x + 0.10)2 

The value for x is very small, so we can approximate and use 0.10 M for 2x + 0.10

  • 1.7 x 10-5 = (x)(0.10)2

  • x = 1.7 x 10-3 M

Additional Note

We can compare this value of to molar solubility of PbCl2 when it is NOT in a solution of 0.10 M NaCl

  • Ksp = [Pb2+ (aq)][Cl– (aq)]2

  • 1.7 x 10-5 = (x)(2x)2 

  • 1.7 x 10-5 = 4x3

  • x = cube root of fraction numerator 1.75 space cross times space 10 to the power of negative 5 end exponent over denominator 4 end fraction end root

  • x = 0.016 M

So we can see that the addition of a common ion (Cl–) decreased the solubility of PbCl2 by roughly a factor of 10

Last updated:

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Solubility-Product ConstantNext:pH & Solubility
    Author
    Reviewer
    Philippa Platt

    Author: Philippa Platt

    Expertise: Chemistry

    Philippa has worked as a GCSE and A level chemistry teacher and tutor for over thirteen years. She studied chemistry and sport science at Loughborough University graduating in 2007 having also completed her PGCE in science. Throughout her time as a teacher she was incharge of a boarding house for five years and coached many teams in a variety of sports. When not producing resources with the chemistry team, Philippa enjoys being active outside with her young family and is a very keen gardener

    Stewart Hird

    Author: Stewart Hird

    Expertise: Chemistry Lead

    Stewart has been an enthusiastic GCSE, IGCSE, A Level and IB teacher for more than 30 years in the UK as well as overseas, and has also been an examiner for IB and A Level. As a long-standing Head of Science, Stewart brings a wealth of experience to creating Topic Questions and revision materials for Save My Exams. Stewart specialises in Chemistry, but has also taught Physics and Environmental Systems and Societies.