Calculating Equilibrium Concentrations (College Board AP® Chemistry)

Study Guide

Written by: Fallon

Calculating Equilibrium Concentrations

The concentration or partial pressure of each species at equilibrium can be determined if all of the following are known:
- The balanced chemical equation
- The initial concentration or partial pressure of each species
- The equilibrium constant (K)
To determine the conditions at equilibrium, we use an ICE table

	Reactant	Product
Initial
Change
Equilibrium

An ICE table can be used to solve for concentrations (M), amounts (mol), or partial pressures (atm)
The initial concentration or partial pressure of each species is typically provided in the question
The change may be indicated in the question, but can also be determined by the stoichiometric coefficients
- Species that are consumed during the course of the reaction will have a change of -x multiplied by the appropriate stoichiometric coefficient
- Species that are produced during the course of the reaction will have a change of +x multiplied by the appropriate stoichiometric coefficient
The equilibrium concentration or partial pressure of each species is the sum of the initial and change values
We then solve for x by substituting the equilibrium values into the appropriate equilibrium expression
Once x is known, we can return to the ICE table to calculate the equilibrium concentrations or partial pressures

Worked Example

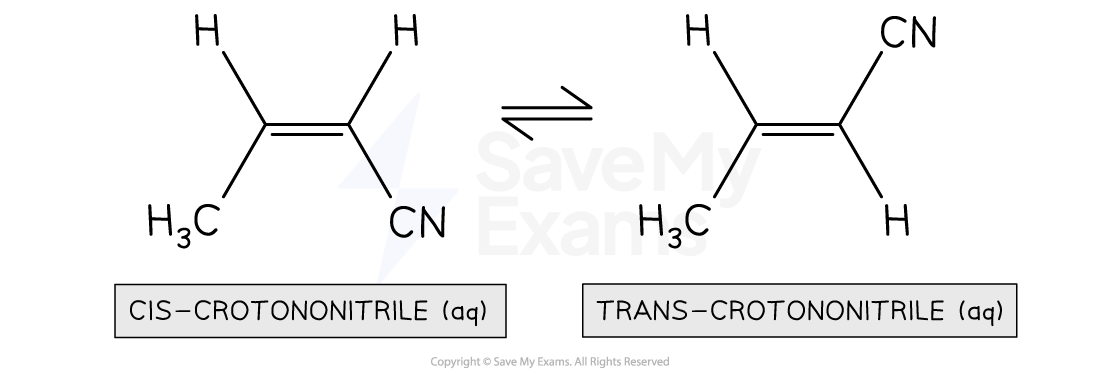
A 2.0 M sample of cis-crotononitrile at 303°C is allowed to come to equilibrium according to the equation above. The equilibrium constant, K_c, for this reaction at 303°C is 1.40. What are the concentrations of cis-crotononitrile and trans-crotononitrile after equilibrium is established?

Answer:

Step 1: Completing an ICE table

The initial concentrations of the cis- and trans- forms are 2.0 M and 0.0 M respectively
In order to reach equilibrium, there must be an overall net conversion of reactants to products as no trans-crotononitrile is initially present
Both stoichiometric coefficients are 1.
We complete the ICE table as shown below

	cis-crotononitrile	trans-crotononitrile
Initial concentration (M)	2.00	0
Change in concentration (M)	-x	+x
Equilibrium concentration (M)	2.00 - x	x

Step 2: Using an equilibrium expression to solve for x

The equilibrium expression for K_c is

$K_{c} = \frac{[trans - crotononitrile]}{[cis - crotononitrile]}$

Substituting the equilibrium constant and equilibrium concentrations into the equation and rearranging to solve for x

$1.40 = \frac{x}{2.00 - x}$

$1.40 \times (2.00 - x) = x$

$2.80 - 1.40 x = x$

$2.80 = 2.40 x$

$\frac{2.80}{2.40} = x$

1.17 M = x

Step 3: Calculating the concentrations at equilibrium

[cis-crotononitrile]_eq = 2.00 M – x

= 2.00 M - 1.17 M

= 0.83 M

[trans-crotononitrile] = x

= 1.17 M

Worked Example

I₂(g) + H₂(g) ⇌ 2HI (g) K_P = 160 at 500 K

Equimolar amounts of I₂(g) and H₂(g) were pumped into a previously evacuated, rigid sealed flask. The gases were allowed to react at 500 K according to the equation above. What is the partial pressure of HI (g) at equilibrium if the initial pressure inside the flask was 12.00 atm?

Answer:

Step 1: Completing an ICE table

Initial partial pressure
- $P_{HI (initial)} = 0 atm$ as no products are initially present
- Equimolar amounts of I₂ and H₂ are initially present, so they must have equivalent mole fractions and therefore equal partial pressures
- $P_{I_{2} (initial)} = P_{H_{2} (initial)} = 6.00 atm$ as the total initial pressure is 12.00 atm
In order to reach equilibrium, there must be an overall net conversion of reactants to products as no HI is initially present
The change in equilibrium must reflect the stoichiometric coefficients
We complete the ICE table as shown below

	I₂	H₂	HI
Initial partial pressure (atm)	6.00	6.00	0
Change in partial pressure (atm)	-x	-x	+2x
Equilibrium partial pressure (atm)	6.00 - x	6.00 - x	2x

Step 2: Using an equilibrium expression to solve for x

The equilibrium expression for K_P is

$K_{P} = \frac{{(P_{HI})}^{2}}{(P_{I_{2}}) (P_{H_{2}})}$

Substituting the equilibrium constant and partial pressures at equilibrium into the equation and rearranging to solve for x

$160 = \frac{{(2 x)}^{2}}{(6.00 - x) (6.00 - x)}$

Note that the right side of the equation is a perfect square

$\sqrt{160} = \sqrt{\frac{{(2 x)}^{2}}{(6.00 - x) (6.00 - x)}}$

$12.649 = \frac{2 x}{6.00 - x}$

$12.649 \times (6.00 - x) = 2 x$

$75.9 - 12.649 x = 2 x$

$75.9 = 14.649 x$

$\frac{75.9}{14.649} = x$

$5.18 atm = x$

Step 3: Calculating the partial pressure of HI at equilibrium

From the ICE table

$P_{HI (eq)} = 2 x$

Substituting x into the equation

$P_{HI (eq)} = 2 \times 5.18 atm$

$P_{HI (eq)} = 10.4 atm$

Examiner Tips and Tricks

Check your calculations by substituting your equilibrium concentrations or partial pressures back into the equilibrium expression. The value you determine for K should be close to the original value given in the question.

Always check the equilibrium expression for perfect squares. Taking the square root of both sides of the equation in these instances allows you to quickly simplify the calculation.

Last updated: 25 August 2024

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Manipulating the Equilibrium ConstantNext:Representations of Equilibrium

Calculating Equilibrium Concentrations (College Board AP® Chemistry)

Study Guide

Calculating Equilibrium Concentrations

Worked Example

Worked Example

Examiner Tips and Tricks

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Fallon

Author: Stewart Hird