Energy Transfers (College Board AP® Chemistry): Study Guide
Conservation of Energy
All forms of energy can be converted from one form to the other, for example:
We feel warm when we stand in sunlight because radiant energy is converted to thermal energy on our skin
When a ball rolls down a hill, the potential energy in the ball is converted to kinetic energy
The batteries which power our devices have the stored chemical energy converted to electrical energy
All of these conversions and transfers proceed in accord with one of the most important observations in science:
Energy can be neither created nor destroyed
During a chemical or physical process, any energy lost by the system must be gained by the surroundings and vice versa
This important observation, that energy is conserved, is known as the first law of thermodynamics
In a thermodynamic sense, this law is summarized as: “the total quantity of energy in the universe is assumed constant”
Internal Energy, E
To apply the first law of thermodynamics to chemical systems, we must consider all sources of energy in the system being studied
These are typically kinetic and potential energy
The internal energy, E, of a system is the sum of all the kinetic and potential energies of the components of the system
We generally do not know the numerical value of a system’s internal energy
However, during a chemical reaction, we can measure the change in internal energy, ΔE, of the system
This is mathematically defined as:
ΔE = Efinal - Eintial
From the above relationship, we can define the direction of energy transfer between the system and surroundings during a physical or chemical change
A positive ΔE value indicates Efinal > Einitial, which means energy is gained by the system from the surroundings
A negative ΔE value indicates Efinal < Einitial, which means the system loses energy to the surrounding
It is important to note that in keeping with the first law of thermodynamics, any increase in the energy of the system is accompanied by a decrease in the energy of the surroundings, and vice versa
Relationship between ΔE, Heat (q) and Work (w)
Any energy exchange between a system and its surroundings is observed in the form of heat or work
Hence, changes in the magnitude of the internal energy, ΔE, of a system could either be in the form of:
Heat added or removed from the system
Work done on or by the system
This relationship allows us to mathematically define the first law of thermodynamics
When a system undergoes any chemical or physical change, the change in internal energy, ΔE, is the sum of the heat added to or released from the system, q, and the work done on or by the system,w
ΔE = q + w
It is important to take note of the sign conventions associated with work and heat in determining the value of ΔE
When heat is gained by the system; q is positive
When heat is lost by the system; q is negative
When work is done by the system; w is negative
When work is done on the system; w is positive
Worked Example
Calculate the change in the internal energy for a process in which a system absorbs 140 J of heat from the surroundings and does 85 J of work on the surroundings
Answer:
Analyze: We are asked to determine the value of ΔE while being provided with the values of q and w
Plan:
We must first determine the signs of q and w
Then we substitute these values into the equation, ΔE = q + w to determine ΔE
Solution:
Step 1:
The system absorbs heat, q = 140 J
The system works on the surroundings, w = -85 J
Step 2: Substitute the values of q and w
ΔE = q + w
ΔE = 140 - 85
ΔE = 55 J
Specific Heat Capacity
All substances change temperature when they are heated
However, the magnitude of the temperature change produced by a given quantity of heat varies from substance to substance
The temperature change experienced by a substance when heat is absorbed is dependent on its heat capacity
Heat capacity, C, is defined as the heat required to raise the temperature of a substance by 1 K or 1℃
The greater the heat capacity of an object, the greater the amount of heat required to produce a given temperature increase
It is measured in J K-1 or J ℃-1
For a pure substance, the heat capacity is defined in terms of a specified amount of the substance
For one mole of a substance, the heat capacity is known as molar heat capacity, Cm
For one gram of a substance, the heat capacity is known as specific heat capacity, Cs
The specific heat capacity of a substance can be experimentally determined using the following variables:
Mass of substance, m
Temperature change ΔT
Quantity of heat, q
The relationship between the specific heat capacity, temperature change, mass of substance and quantity of heat is mathematically defined as:
Cs = q / m × ΔT
On rearranging, we can express q as:
q = m × Cs× ΔT
Specific heat capacity is measured in J g-1 ℃-1 or J g-1 K-1
Molar heat capacity is measured in J mol-1 ℃-1 or J g-1 K-1
Examiner Tips and Tricks
Don’t waste your time…remember
Temperature change, ΔT, may be measured in either K (kelvins) or ℃ (degree Celsius)
The temperature change will be the same regardless of the units
Therefore, there is no need to convert initial and final temperatures before finding the temperature change
Worked Example
How much heat is transferred to a 20.0 g piece of iron initially at a temperature of 20.0 °C when placed in boiling water? Assume the temperature of the water is 100.0 °C and that was the final temperature of the iron. The specific heat of iron is 0.449 J g-1 ℃-1
Answer:
Analyze: We are asked to determine the heat required to raise 20.0 g of iron from 20.0 ℃ to 100.0 ℃
Plan: Find the change in temperature, ΔT and substitute the given values into the expression for q
Solution:
Step 1: Calculate the temperature change, ΔT
ΔT = Tfinal - Tinitial
ΔT = 100 - 20
ΔT = 80.0 ℃
Step 2: Determine, q, using the formula
q = m × Cs × ΔT
q = 20.0 × 0.44 × 80.0
q = 704 J
Worked Example
Consider the following data:
Metal | Al | Fe |
Specific Heat Capacity | 0.900 | 0.449 |
Temperature | 40 | 60 |
Mass | 10 | 30 |
Which of the following will take place when these two metals are placed in contact?
Heat will flow from Al to Fe because Al has a larger specific heat capacity
Heat will flow from Fe to Al because Fe has a larger mass
Heat will flow from Fe to Al because Fe has a smaller specific heat capacity
Heat will flow from Fe to Al because Fe is at a higher temperature
Answer:
Option D is correct because:
Heat will always flow from a body at a higher temperature to one at a lower temperature
The flow of heat is independent of the mass or specific heat capacity
Options A and C are incorrect because:
The flow of heat is not dependent on the specific heat capacity but on the temperature difference
Option B is incorrect because:
The flow of heat is not dependent on the mass of the substance but the temperature difference
Energy Changes of a System
Changes in the energy of a system can be explained by phase transitions which occur in the system
Important phase transitions which can be used to demonstrate energy changes that occur from the heating and cooling of a system include:
Melting / Freezing
Evaporation / Condensation
Sublimation / Deposition
Energy and Phase Changes
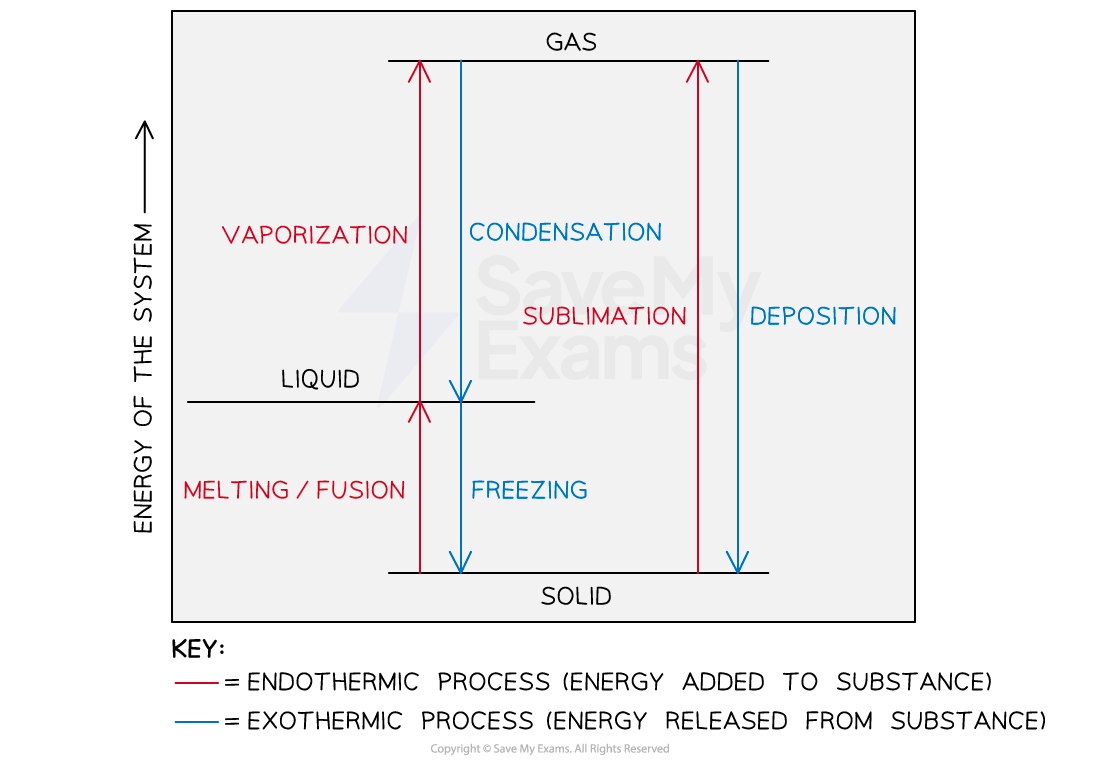
A graphical representation of the effect of energy changes in a system and the change in the state of matter
Melting/Freezing
The particles in a solid system are arranged in more or less fixed positions with respect to one another and closely arranged to minimize the energy of the system
When heat is added to this system, the temperature of the solid increases
This increases the kinetic energy of the particles until they are able to move relative to one another
Consequently, the solid begins the process of melting
The temperature at which this occurs is known as the melting point
Melting is also known as fusion and the amount of heat required for this process is known as the heat of fusion
For example, the heat of fusion for ice is 6.01 kJ/mol
On the other hand, in a liquid system, the cooling of the system will result in a decrease in the temperature of the liquid
This results in a decrease in the energy of the particles and the change of the liquid to a solid
This process is referred to as freezing
For a particular substance, the amount of energy/heat required for freezing is equal to its heat of fusion
In general,
The process of melting involves an increase in the energy of the system and is considered to be endothermic
The freezing process involves a decrease in the energy of the system and is considered to be exothermic
Evaporation/Condensation
Similar to the process of melting, heating a liquid system increases the energy of the system
The particles of the liquid will experience an increase in their kinetic energy
This process is known as evaporation and the heat required for this is known as the heat of vaporization
The heat of vaporization is used to measure the strength of intermolecular forces that exist within the liquid
It is important to differentiate between evaporation and boiling
Evaporation is slower and occurs at the surface of the liquid
Boiling is faster and occurs throughout the liquid
Evaporation results in cooling while boiling does not
For example, we feel cool when we step out of a swimming pool or a warm shower because the water’s heat of vaporization is drawn from our bodies when it evaporates from our skin
Condensation describes the process by which a gas is changed to a liquid
It occurs as a result of a decrease in the energy of the gas particles
For example, dew is formed by the condensation of liquid water in the atmosphere
In general, for any given substance:
The heat of condensation is equal in magnitude to the heat of vaporization but opposite in sign
Heat of condensation is exothermic and negative while vaporization is endothermic and positive
Sublimation/Deposition
Sublimation describes the process by which the particles of solids are directly converted to gas without going through the liquid phase
For example, solid iodine molecules are converted to gas when heated
The heat of sublimation is the sum of the heat of vaporization and the heat of fusion
Hsub = Hvaporization + Hfusion
On the other hand, the process by which gas molecules are converted to solids is known as deposition
Frost is solid water formed by direct condensation of water vapor from the atmosphere without first forming liquid water
Snow is formed by a similar process in the upper atmosphere
Similar to the heat of condensation and vaporization
The heat of deposition is an exothermic process
The heat of sublimation is an endothermic process
The heat of deposition is equal in magnitude but opposite in sign to the heat of sublimation
Changing Chemical Systems
Energy changes in chemical systems are observed through three processes:
Heating/Cooling
Phase Transition
Chemical Reaction
Heating/Cooling Curves
When heat is added at a constant rate to a solid material at a temperature below its melting point, the following effects are observed:
A constant rate of increase in the temperature of the solid until it begins to melt
During this process, there is an increase in the average kinetic energy of the particles while the potential energy decreases
When melting begins, the temperature remains constant until all of the solid is converted to liquid
A constant temperature shows that the kinetic energy of the particles remains constant while the potential energy increases
The heat added is used to overcome the intermolecular forces present in the substance
The temperature of the liquid starts increasing at a constant rate until it starts to boil
Similar to the beginning of the heating process, the average kinetic energy of the particles increases as more heat is added
When boiling begins, the temperature remains constant until all of the liquid is converted to gas
Again, the average kinetic energy remains the same as the heat added is used to break the intermolecular forces in the particles of the liquid
The temperature of the gas, then, increases at a constant rate
All of these processes can be summarized in a heating curve as shown below:
Heating Curve
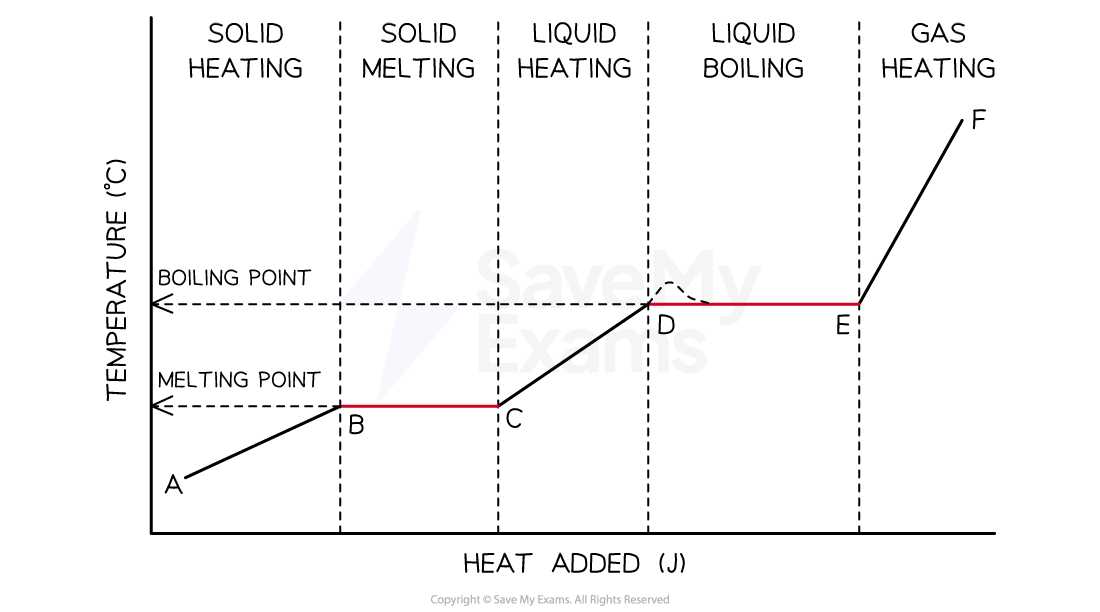
Diagram of a typical heating curve of a sample from the solid state on the left to the gaseous state on the right. The temperature of the sample increases as heat is added except during the change of phase which are represented by segments BC and DE
From segments AB, CD and EF of the heating curve
Heat added only raises the temperature and can be calculated from the product of the specific heat capacity, the mass and the temperature change; q = m × Cs× ΔT
The slope of these lines can be used to compare the specific heat capacities of the solid, liquid and gaseous phases of the sample
The greater the specific heat capacity, the less the slope of the line
This means that more heat is required to change the given quantity of the sample by one degree
This would observed on the heating curve for water where the specific heat capacity of liquid water is greater than ice
In segments BC and DE
The temperature remains constant during these phase changes because the added energy is used to overcome the attractive forces between molecules rather than to increase their average kinetic energy
The heat involved during these processes is known as the heat of fusion and the heat of vaporization respectively
The longer the lines, the greater the value of heat required to change the phase
Generally, the heat of vaporization is greater than the heat of fusion
This is because gas molecules have the biggest intermolecular space and the force of attraction between them is nearly non-existent
A cooling curve is the reverse of a heating curve with similar features except we start with a gas sample and end with a solid
Cooling involves the process of removing heat from the sample
Chemical Reactions
Many chemical reactions are accompanied by heat exchange between the system and the surroundings
Consider a system in which a chemical reaction occurs
Before the reaction, the system and surroundings are at the same temperature, say 25℃
As soon as the reaction begins, the temperature changes
If there’s a decrease in the temperature of the system, then energy flows from the surroundings to the system
The system has absorbed heat and q is positive
When the reaction stops, heat continues to flow until the system returns to the temperature of its surroundings
If there’s an increase in the temperature of the system, then energy flows from the system to the surroundings
In this case, the system has evolved heat and q is negative
Worked Example
The graph below represents the uniform heating of a sample of a substance starting as a solid below its melting point

Which statement describes what happens to the energy of the particles of the sample during time interval DE?
Average kinetic energy remains the same and potential energy increases
Average kinetic energy remains the same and potential energy decreases
Average kinetic energy decreases and potential energy remains the same
Average kinetic energy increases and potential energy remains the same
Answer:
Option A is correct because:
At time interval BC, the temperature of the substance is constant which means the average kinetic energy remains the same
However, the potential energy of the system increases because the added heat energy during a change of phase is stored as potential energy
Option B is incorrect because:
During phase change, potential energy increases because the added heat energy is stored as potential energy
Options C and D are wrong because:
The constant temperature indicated by the line BC shows a constant average kinetic energy while potential energy changes

Unlock more, it's free!
Did this page help you?