Manipulating Concentration-Time Graphs (College Board AP® Chemistry)

First Order Concentration-Time Graphs

• As shown in the previous section, the concentration vs time graph for a first order reaction is not a straight line

  • However, line equations are easier to interpret because they have a constant slope

• The rate equation for a first order reaction is shown below:

Rate = k[A]

• Since the rate is the change in concentration of the reactant per unit of time, the rate equation can be transformed in:

• Remember that the change from the reactant must have a negative sign

• Using a mathematical operation called integration a new rate equation can be constructed

  • The name of this new equation is the integrated rate law for a first order reaction

ln [A]_t – ln [A]₀ = – kt 

• This equation links the concentration of A at any time (), with the initial concentration of A (), the rate constant (k), and the time (t)

  • It can be used to calculate the concentration of A at any time, just by replacing the time

  • The initial concentration of A and the rate constant are always the same and they, in some cases, given by the statement

• If the new rate equation is rearranged, the following equation is obtained:

ln [A]_t  = – kt  +  ln [A]₀

• This new equation is equivalent to the equation of an straight line:

y = mx + c

• Comparing carefully both equations, if  ln [A]_t is plotted against t, an straight line going down is obtained

  • The slope of the straight line is -k

  • The y-intercept of the line is ln [A]₀

The concentration-time graph and the integrated rate law graph for a first order reaction

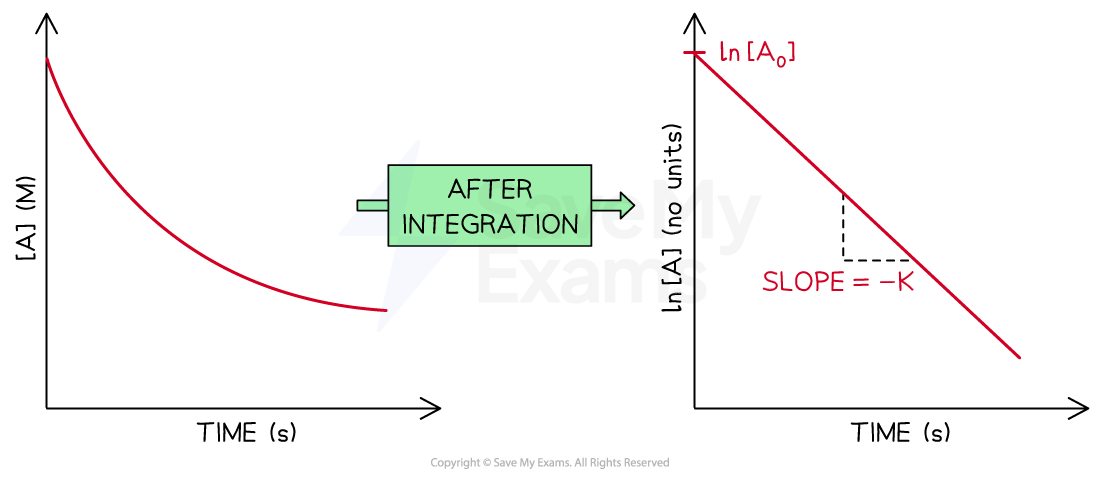
Diagram showing the difference between a concentration-time graph and the graph after the integration to obtain the integrated rate law for a first order reaction. The elements of the integrated rate law graph are labeled

Second Order Concentration-Time Graphs

• As shown in the previous section, the concentration vs time graph for a second order reaction is not a straight line

  • However, line equations are easier to interpret because they have a constant slope

• The rate equation for a first order reaction is shown below:

Rate = k [A]²

• Since the rate is the change in concentration of the reactant per unit of time, the rate equation can be transformed in:

• Remember that the change from the reactant must have a negative sign

• Using a mathematical operation called integration a new rate equation can be constructed

  • The name of this new equation is the integrated rate law for a second order reaction

• This equation links the concentration of A at any time (), with the initial concentration of A (), the rate constant (k), and the time (t)

  • It can be used to calculate the concentration of A at any time, just by replacing the time

  • The initial concentration of A and the rate constant are always the same and they are, in some cases, given by the statement

• If the new rate equation is rearranged, the following equation is obtained:

• This new equation is equivalent to the equation of an straight line:

y = mx + c

• Comparing carefully both equations, if   is plotted against t, an straight line going up is obtained

  • The slope of the straight line is k

  • The y-intercept of the line is 

The concentration-time graph and the integrated rate law graph for a second order reaction

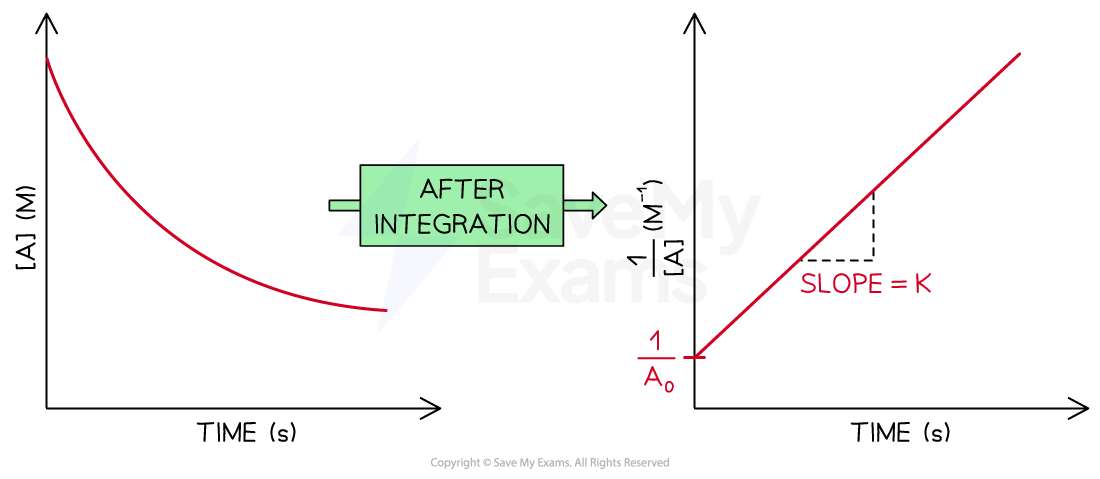
Diagram showing the difference between a concentration-time graph and the graph after the integration to obtain the integrated rate law for a second order reaction. The elements of the integrated rate law graph are labeled