AP®ChemistryCollege BoardStudy GuidesUnit 5: KineticsReaction RatesIntroduction to Rate Law

Introduction to Rate Law (College Board AP® Chemistry)

Study Guide

Test yourself
Martín

Written by: Martín

Reviewed by: Stewart Hird

Rate Law

Experimental data and the rate of reaction

  • One way to study the effect of concentration on the rate is monitoring the rate of reaction against the concentration of the reactant

  • The following general reaction will be used as example

D → E + F

  • The rate of reaction at different concentrations of D was tabulated and plotted

[D] (M)

Rate (M s-1)

3.00

2.000 x 10-3

2.00

1.334 x 10-3

1.00

6.670 x 10-4

 

  • A line is plotted and the gradient of the line is calculated using the formula below

gradient space equals space fraction numerator increment straight y over denominator increment straight x end fraction

Graph to show rate against [D]

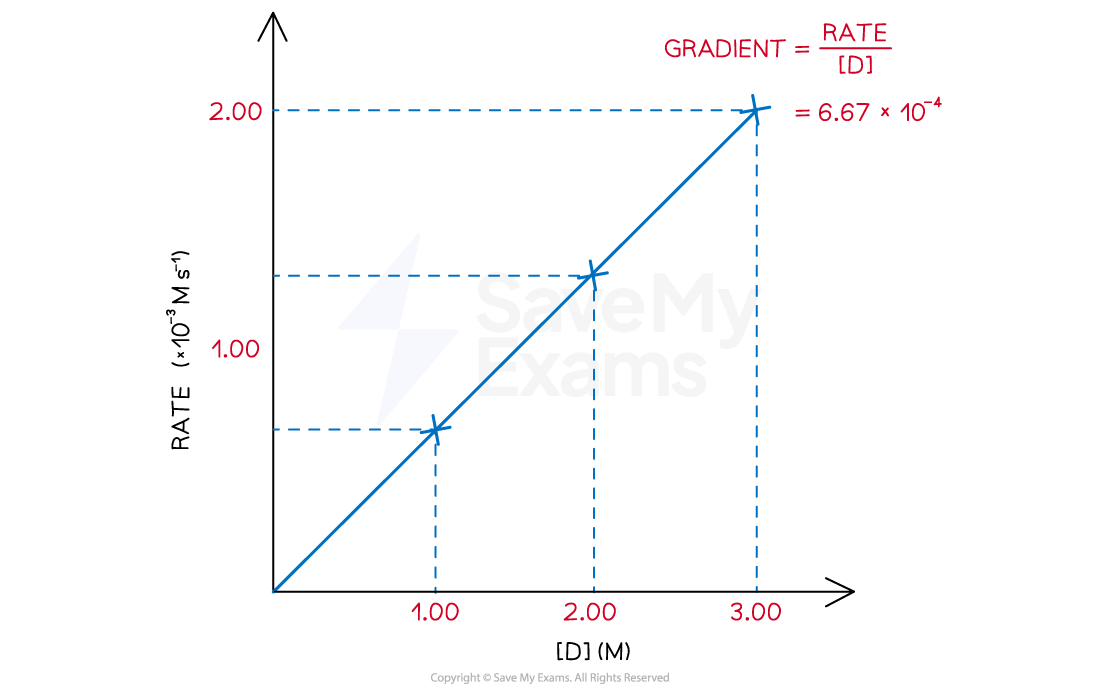
rate-vs-concentration-graph

Rate of reaction over various concentrations of D

  • As shown in the diagram, there is a directly proportional relation between the rate of reaction and the concentration of D

  • This relation can be written as a mathematical equation as shown below

Rate ∝ [D]

Rate = k [D]

  • This equation means that if the concentration of D doubles, the rate will double

  • The constant of proportionality (k) is called the rate constant

    • The units of the rate constant can be used to determine the order of the reaction

The rate equation

  • The following general reaction will be used to discuss the rate equation:

A +B → C+D

  • The general rate equation is:

Rate = k [A]m [B]n

  • Where:

    • [A] and [B] are the concentration of reactants

    • m and n are the orders with respect to each reactant

  • The rate of the reaction will depend on the mechanism of reaction and it can only be found experimentally

  • Intermediate products do not feature in rate equations

The order of reactants

  • The order of reactants shows how the concentration of a reactant affect the rate

    • It is represented as the power to which the concentration is raised in the rate equation

  • The most common orders are listed below:

  • Zero order occurs when the order respect to a chemical is 0

    • This means that changing the concentration has no effect on the rate

    • Therefore, it is not included in the rate equation

  • First order occurs when the order respect to a chemical is 1

    • This means that the concentration is directly proportional to the rate

    • E.g. Doubling the concentration will double the rate

  • Second order occurs when the order respect to a chemical is 2

    • This means the that square of the concentration is directly proportional to the rate 

    • E.g. Doubling the concentration will increase the rate by a factor of 4 since 22 is 4

  • Overall order  is just the sum of the powers of the reactants that appear in the rate equation

Worked Example

The chemical equation for the thermal decomposition of dinitrogen pentoxide is:

2N2O5 (g) → 4NO2 (g) + O2 (g)

The rate equation for this reaction is:

Rate = k [N2O5 (g)]

  1. State the order of reaction with respect to nitrogen pentoxide

  2. State the overall order of reaction

  3. Deduce the effect on the rate of reaction if the concentration of dinitrogen pentoxide is doubled

  4. Determine the units of the rate constant

Answers:

Answer 1:

  • Dinitrogen pentoxide features in the rate equation, therefore, it cannot be order zero

  • The dinitrogen pentoxide is not raised to a power, which means that it cannot be order 2

  • Therefore, the order with respect to dinitrogen pentoxide must be order 1

Answer 2:

  • The overall order is just the sum of all the powers in the rate equation. Since, dinitrogen pentoxide is the only reactant and it is raised to the power of 1. The overall order is first order

Answer 3:

  • Since the overall order is first order, the concentration of dinitrogen pentoxide is directly proportional to the rate

  • This means that if the concentration of the dinitrogen pentoxide is doubled, then the rate of reaction will be the double

Answer 4:

  • Units space of space rate space equals space left parenthesis units space of space rate space constant right parenthesis space cross times space left parenthesis units space of space concentration space of space straight N subscript 2 straight O subscript 5 right parenthesis

  • Rearranging the equation,

  • Units space of space rate space constant space equals fraction numerator Units space of space rate over denominator Units space of space concentration space of space straight N subscript 2 straight O subscript 5 end fraction space

  • Units space of space rate space constant space equals space fraction numerator M space straight s to the power of negative 1 end exponent over denominator M end fraction space equals straight s to the power of negative 1 end exponent

Examiner Tips and Tricks

The overall order of the reaction can be inferred from the units of the rate constant. If the rate is measure per second:

  • Rate constant units of a zero order reaction are M s-1

  • Rate constant units of a first order reaction are s-1

  • Rate constant units of a second order reaction are M-1 s-1

Initial Rates & Orders of Reaction

  • The order of the reactants can be determined with experimental data from the the initial rates of reaction

    • This information is usually displayed in a table

  • The following steps must be followed to determine the order for each reactant:

  1. Identify two experiments where the concentration of this reactant changes, but the concentration of the other reactants is the same

  2. Identify what has happened with the concentration

  3. Determine the effect of the concentration in the rate of reaction

  4. Deduce the order of reaction

  5. Repeat this procedure with all the reactants one at the time

  • Once all the orders are determined the rate equation can be built

    • Zero order reactants are not included

    • First order reactants are included and do not require a power (it is the s

    • Second order reactants are raised to the power of 2

Examiner Tips and Tricks

Determining the orders for each reactant is one of the most assessed tasks regarding kinetics, so it's worth spending time to get to know this topic well 

Worked Example

(CH3)3CBr  +  OH-  →  (CH3)3COH  +  Br-

The table show experimental data for the reaction above

Experiment

Initial [(CH3)3CBr] /

M

Initial [OH-] /

M

Initial rate of reaction /

M  s-1

1

1.0 x 10-3

2.0 x 10-3

3.0 x 10-3

2

2.0 x 10-3

2.0 x 10-3

6.0 x 10-3

3

1.0 x 10-3

4.0 x 10-3

1.2 x 10-2

4

1.5 x 10-3

4.0 x 10-3

4.5 x 10-3

 

Determine the rate equation for this reaction

Answer:

Order with respect to (CH3)3CBr

  1. In experiments 1 and 2, the concentration of (CH3)3CBr changes while the concentration of OH- remains constant

  2. The [(CH3)3CBr] has doubled

  3. The rate of the reaction has also doubled

  4. Therefore, the order with respect to [(CH3)3CBr] is 1 (first order)

 left square bracket Change space in space concentration right square bracket to the power of order equals change space in space rate

begin mathsize 16px style open square brackets 2 close square brackets to the power of order space equals space 2 end style

open square brackets 2 close square brackets to the power of 1 space equals space 2

order = 1

Order with respect to OH-

  1. In experiments 1 and 3, the concentration of OH- changes while the concentration of (CH3)3CBr remains constant

  2. The [OH-] has doubled

  3. The rate of the reaction has increased by a factor of 4

  4. Therefore, the order with respect to [OH-] is 2 (second order)

 left square bracket Change space in space concentration right square bracket to the power of order equals change space in space rate

stretchy left square bracket 2 stretchy right square bracket to the power of order space equals space 4

[2]2 = 4

order = 2

Building the rate equation

Rate = k [(CH3)3CBr]m [OH-]n

Replacing the orders,

Rate = k [(CH3)3CBr] [OH-]2

Last updated:

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Factors Affecting Reaction RateNext:Concentration-Time Graphs
    Author
    Reviewer
    Martín

    Author: Martín

    Expertise: Chemistry Content Creator

    Martín, a dedicated chemistry teacher and tutor, excels in guiding students through IB, AP, and IGCSE Chemistry. As an IB Chemistry student, he came from hands-on preparation, focusing on practical exam techniques and rigorous practice. While at Universidad San Francisco de Quito, his academic journey sparked a passion for computational and physical chemistry. Martín specializes in chemistry, and he knows that SaveMyExams is the right place if he wants to have a positive impact all around the world.

    Stewart Hird

    Author: Stewart Hird

    Expertise: Chemistry Lead

    Stewart has been an enthusiastic GCSE, IGCSE, A Level and IB teacher for more than 30 years in the UK as well as overseas, and has also been an examiner for IB and A Level. As a long-standing Head of Science, Stewart brings a wealth of experience to creating Topic Questions and revision materials for Save My Exams. Stewart specialises in Chemistry, but has also taught Physics and Environmental Systems and Societies.