Concentration-Time Graphs & Rate Constants (College Board AP® Chemistry)

Study Guide

Test yourself

Written by: Martín

Reviewed by: Stewart Hird

Concentration-Time Graphs & Rate Constants

Line equations for the Concentration-Time Graphs

Zero order concentration-time graph is a straight line
- The equation for this line is:

${[A]}_{t} - {[A]}_{0} = - kt$

This equation links the concentration of A at any time (), with the initial concentration of A (), the rate constant (k), and the time (t)
- It can be used to calculate the concentration of A at any time, just by replacing the time
If the line equation is rearranged, the following equation is obtained:

${[A]}_{t} = - kt + {[A]}_{0}$

Looking carefully into the equation, if [A]_t is plotted against t, an straight line going down is obtained
- The slope of the straight line is -k
- The y-intercept of the line is [A]₀
An straight line can be drawn for a first order reaction by using the integrated law for a first order reaction
- The equation for the integrated law is shown below in two equivalent ways:

ln [A]_t- ln [A]₀ = -kt

ln [A]_t = -kt +ln [A]₀

An straight line can be drawn for a second order reaction by using the integrated law for a second order reaction
- The equation for the integrated law is shown below in two equivalent ways:

$\frac{1}{{[A]}_{t}} - \frac{1}{{[A]}_{0}} = kt$

$\frac{1}{{[A]}_{t}} = kt + \frac{1}{{[A]}_{0}}$

Line equations for zero order, first order and second order reactions

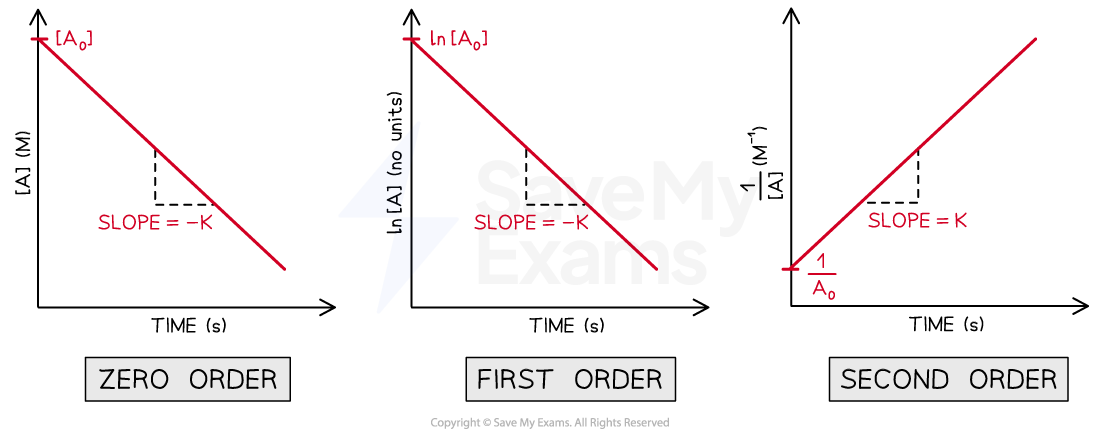
line-equations-for-the-three-orders-of-reaction

Comparison of the axis labels, slopes and y-intercepts between the line equations for a zero order, first order and second order reaction

Worked Example

A student carried the following reaction at the laboratory:

A+B → products

After performing the experiment, the student has plotted the following graphs,

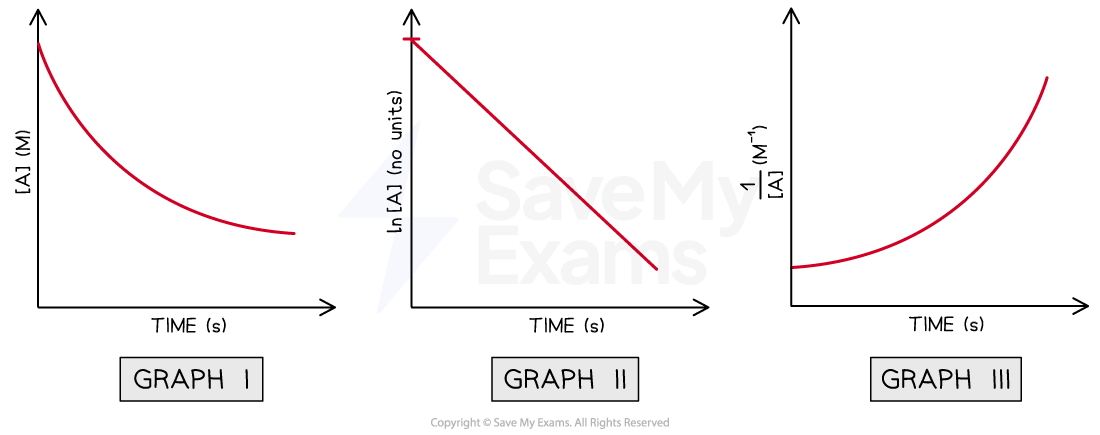
Using the graphs above, determine the order of reaction with respect to A

Answer:

The only graph from these three that is an straight line is Graph II
The axis from this graph are ln[A] vs time
By comparing the three straight line equations, the order of the reaction with respect to [A] must be 1 because it is the only one in which ln[A] is present

ln [A]_t = -kt + ln [A]₀

Therefore, it is a first order reaction with respect to A

The importance of the slope in concentration-time graphs

The slope in concentration-time graphs determine the rate constant of the reaction
- The formula for the slope/gradient is:

$gradient = \frac{∆ y}{∆ x}$

Therefore, if the overall order of reaction is determined, the rate constant can be obtained by calculating the slope of the concentration-time graphs
- For a zero-order reaction, plotting the concentration of reactant vs time

[A]_t versus t

For a first-order reaction, using a plot natural logarithm of the concentration of reactant vs time

ln [A]_t versus t

For a second-order reaction, plotting the inverse of the concentration of reactant vs time

$\frac{1}{{[A]}_{t}} versus t$

Worked Example

A student carried the following reaction at the laboratory:

A+B → products

The student knows it is a zero order with respect to B. She has plotted the following graph:

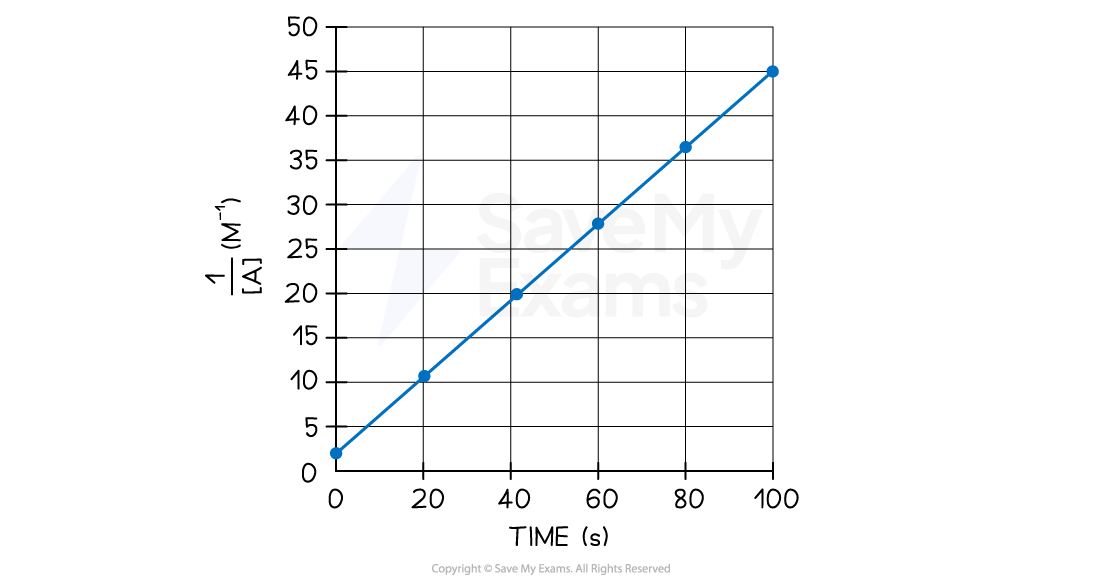
worked-example-rate-constant-determination

Using the graph above, determine the rate constant and write the general rate equation for the reaction

Answer:

Step 1: Determine the order of reaction respect to A
- The axis from this graph are 1/[A] vs time
- By comparing the three straight line equations, the order of the reaction with respect to [A] must be 2 because it is the only one in which 1/[A] is present

$\frac{1}{{[A]}_{t}} = kt + \frac{1}{{[A]}_{0}}$

Therefore, it is a second order reaction with respect to A
Step 2: Determine the overall order of reaction
- Since the statement establishes that it is a zero order reaction respect to B, the overall order is 2
- Therefore, the general rate equation should look like this:

rate =k [A]²

Step 3: Choose two points and write down their coordinates
- Point 1 (0, 2.5)
- Point 2 (80, 37.5)
Step 4: Calculate the slope/gradient using the coordinates
- $gradient = \frac{∆ y}{∆ x}$
- $gradient = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$
- $gradient = \frac{37.5 - 2.5}{80 - 0}$
- gradient = 0.434
Step 5: Calculate the units for the rate constant
- $rate = k {[A]}^{2}$
- $units of rate = (units of k) \times {(units of concentration of A)}^{2}$
- $units of k = \frac{units of rate}{{(units of concentration of A)}^{2}}$
- $units of k = \frac{{Ms}^{- 1}}{{(M)}^{2}}$
- $units of k = \frac{{Ms}^{- 1}}{(M) (M)}$
- $units of k = \frac{s^{- 1}}{M}$
- units of k = M^-1 s^-1
Step 6: Write down the final rate equation by replacing the calculated value for k
- rate = k [A]²
- rate = (0.434 M^-1 s^-1) [A]²

Last updated: 22 August 2024

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Manipulating Concentration-Time GraphsNext:Concentration-Time Graphs & Half-Life

Concentration-Time Graphs & Rate Constants (College Board AP® Chemistry)

Study Guide

Concentration-Time Graphs & Rate Constants

Line equations for the Concentration-Time Graphs

Line equations for zero order, first order and second order reactions

Worked Example

The importance of the slope in concentration-time graphs

Worked Example

You've read 0 of your 10 free study guides

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Martín

Author: Stewart Hird