Concentration-Time Graphs & Half-Life (College Board AP® Chemistry)
Study Guide
Written by: Oluwapelumi Kolawole
Reviewed by: Stewart Hird
Concentration-Time Graphs & Half-Life
Half-life of First Order Reactions
The half life, t1/2, of a reaction is the time taken for the concentration of the reactant to decrease to half its initial concentration
It is a convenient way to determine how fast a reaction is, especially for first order reactions
For a first order reaction, t1/2, is dependent only on rate constant (k) and given as:
t1/2 = 0.693/k
It remains constant throughout the reaction
For example, the half-life of the decomposition of dinitrogen pentoxide, which follows a first order kinetics, can be illustrated graphically
Concentration-Time Graph For a First Order Reaction
A graph showing the constant half-life of a first order reaction.
Radioactive decays are good examples of reactions that follow the first order kinetics
The half-life of radioisotopes can be used to interpret the level of radiation of the radioisotope, for example:
Uranium- 238 has a very long half-life (4.5 × 109 yrs), so it gives off radiation very slowly
While fermium-258 decays with a half-life of 3.8 × 1024 s has a very high decay rate
Half-life of Zero and Second Order Reactions
For zero order and second order reactions, the half-life changes as the reaction progresses
Half-life depends on the initial concentration of reactant
The lower the initial concentration, the longer the half-life
For a zero order reaction, the relationship between t1/2 and initial concentration is given as:
t1/2 = [A]initial / 2k
For a second order reaction, the relationship between t1/2 and initial concentration is given as:
t1/2 = [A]initial / k
Graphical Representations of Half-Life for Zero and Second Order Reactions
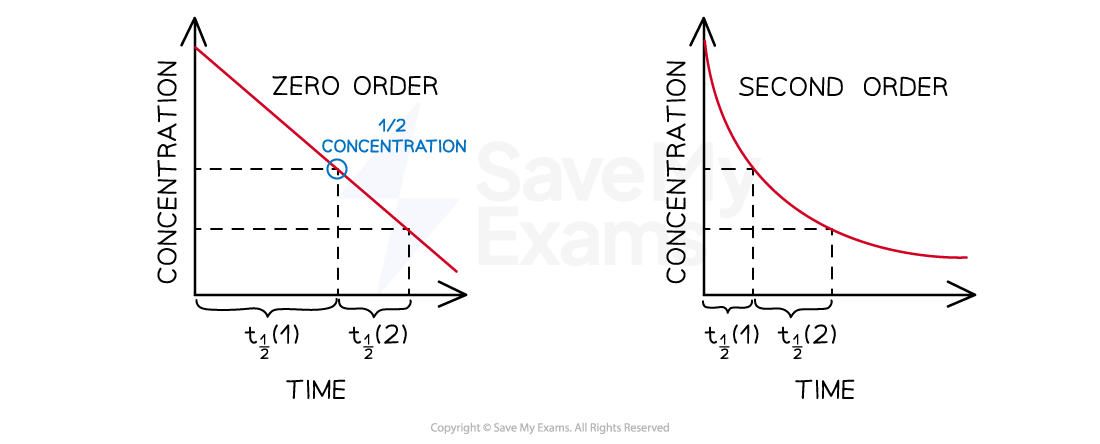
The value for the half life of zero and second order reaction change and are dependent on the initial concentration
Worked Example
The equation for the decomposition of dinitrogen pentoxide when heated in carbon tetrachloride is given below:
N2O5 (g) → 2NO2(g) + ½ O2(g)
If the rate constant for the decomposition of N2O5 is 6.2 ×10-4 /min, what is the half-life?
Answer:
Analyze:
We are given the rate constant for reaction and asked to determine the half-life
Plan:
First, we need to determine the order of the reaction from the unit of the rate constant.
For first order reactions, the units of k include s-1, min-1 and hr-1)
Substitute the k value into the t1/2 expression for a first order reaction
Solution:
t1/2 = 0.693/k
t1/2 = 0.693/6.2 ×10-4
t1/2 = 1.12 × 103 mins
Examiner Tips and Tricks
Watch out for the unit of rate constant to help determine the order of the reaction when you’re not expressly told.
Remember: Rate is measured per unit time, e.g. per second, s-1
So, when the rate is measured per second:
Rate constant, k, units of a zero order reaction are M s-1
Rate constant, k, units of a first order reaction are s-1
Rate constant, k, units of a second order reaction are M-1 s-1
Last updated:
You've read 0 of your 10 free study guides
Unlock more, it's free!
Did this page help you?
