Collision Model (College Board AP® Chemistry)

Molecular Collisions

• On a molecular level, the effect of temperature and concentration can be better understood by the collision model

• The key idea of the collision model is that molecules must collide to react

• Basically, the greater the number of collisions between molecules per second, the faster the reaction

  • Hence, when the concentration of reactants increases, the number of collisions increases resulting in an increased rate of reaction

• According to the kinetic-molecular theory, increasing the temperature increases the average kinetic energy of the molecules

  • This makes the molecules move faster, colliding more frequently and with more energy which then means a faster reaction rate

• An increase in the surface area of solid reactants also increases the reaction rate

  • As a result of the increase in the number of contact points for collision and the consequent increase in the frequency of collision

• However, it is important to note that not every collision between reactant molecules results in product formation

  • Collisions which result in reactions are said to be effective collisions and possess two characteristics:

• Reacting molecules must collide with sufficient energy greater or equal to some minimum energy known as the activation energy (kinetic energy factor)

• Reacting molecules are properly oriented towards each other (orientation factor)

Orientation Factor

• The relative orientations of the molecules during collision determine whether the atoms are suitably positioned to form new bonds

  • Essentially, molecules have to be in the correct position to react

• Consider the reaction between CO and NO₂ to form CO₂ and NO:

  • The reaction only happens when the carbon atom of the CO molecule strikes an oxygen atom of the NO₂ molecule

Orientation Factor and Effective Collision

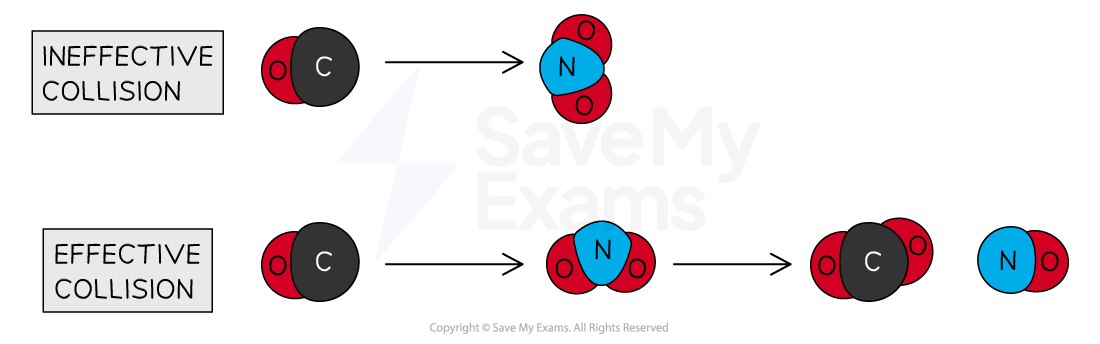
Diagram showing the effect of proper orientation of colliding molecules for a successful reaction. In the reaction between CO and NO₂, a successful collision is obtained when the carbon atom of the CO strikes the oxygen atom of the NO₂.

• According to the collision model, the rate constant, k, which indicates the rate of a reaction, is a product of three factors:

  • Z, the collision frequency, which gives the number of molecular collisions occurring in unit time at unit concentrations of reactants

  • f, the fraction of collisions having energy greater than the activation energy

  • p, the steric factor, which accounts for the fraction of collisions that occur with the reactant molecules properly oriented

• With this, the collision model can be made quantitative with the expression:

k = p × Z  ×  f

Maxwell-Boltzmann Distribution Curves

• One very important factor that brings about a high number of effective collisions is the kinetic energy of reactant molecules

• Reactant molecules are held together by strong chemical bonds

  • When molecules collide, they must be moving rapidly enough to supply the required energy to break these bonds

  • Molecules with small kinetic energies bounce off one another without a reaction

Kinetic Energy and Effective Collision

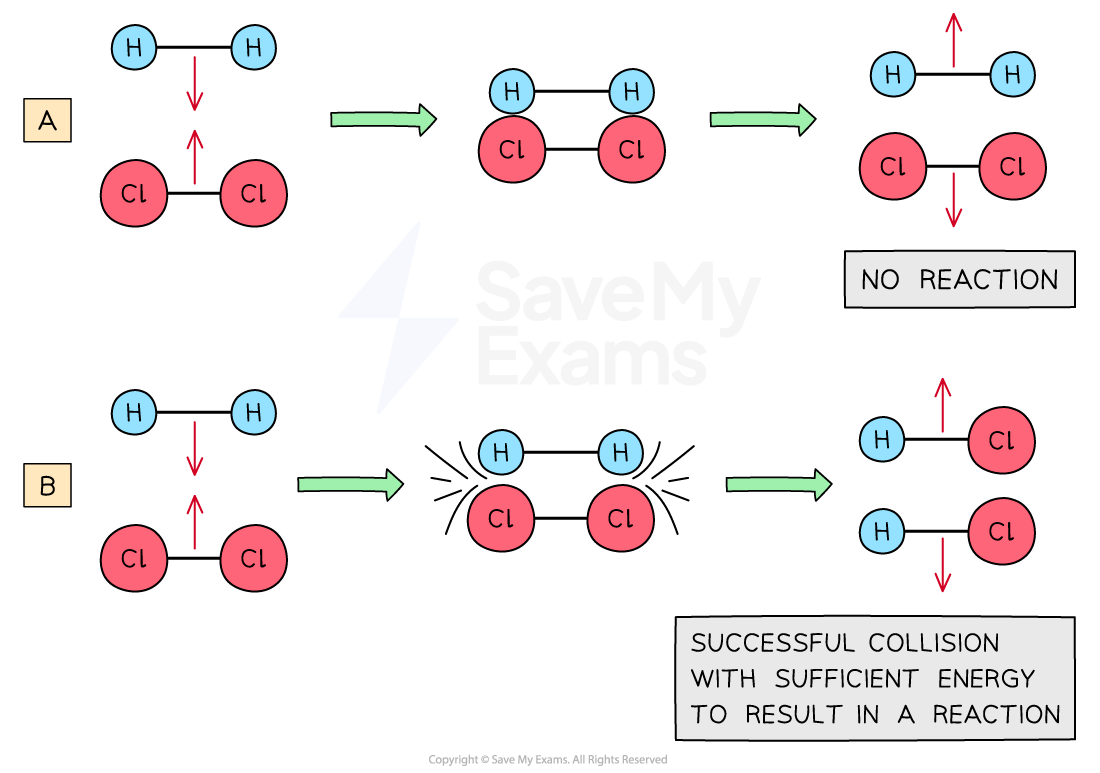
Diagram (A) shows an ineffective collision due to the particles not having enough energy whereas (B) shows an effective collision where the particles have the correct orientation and enough energy for a chemical reaction to take place

• The minimum energy which the reactant molecules must produce on collision in order to initiate the reaction is known as the activation energy, E_a

  • It is a positive quantity, measured in kJ/mol

Maxwell-Boltzmann Distribution, Temperature and Activation Energy

• The effect of temperature on reaction rate can be explained using the kinetic molecular theory

  • Remember: An increase in temperature increases the fraction of molecules with high velocity and hence high kinetic energy

  • A higher temperature means a larger fraction of molecules that can provide the activation energy required for the reaction

• The relationship between the energies of colliding molecules and the activation energy required for a reaction at a certain temperature is described by a Maxwell-Boltzmann distribution curve

  • This curve can be used to qualitatively estimate the fraction of molecules with sufficient energy that results in a reaction

Maxwell-Boltzmann Distribution Curve

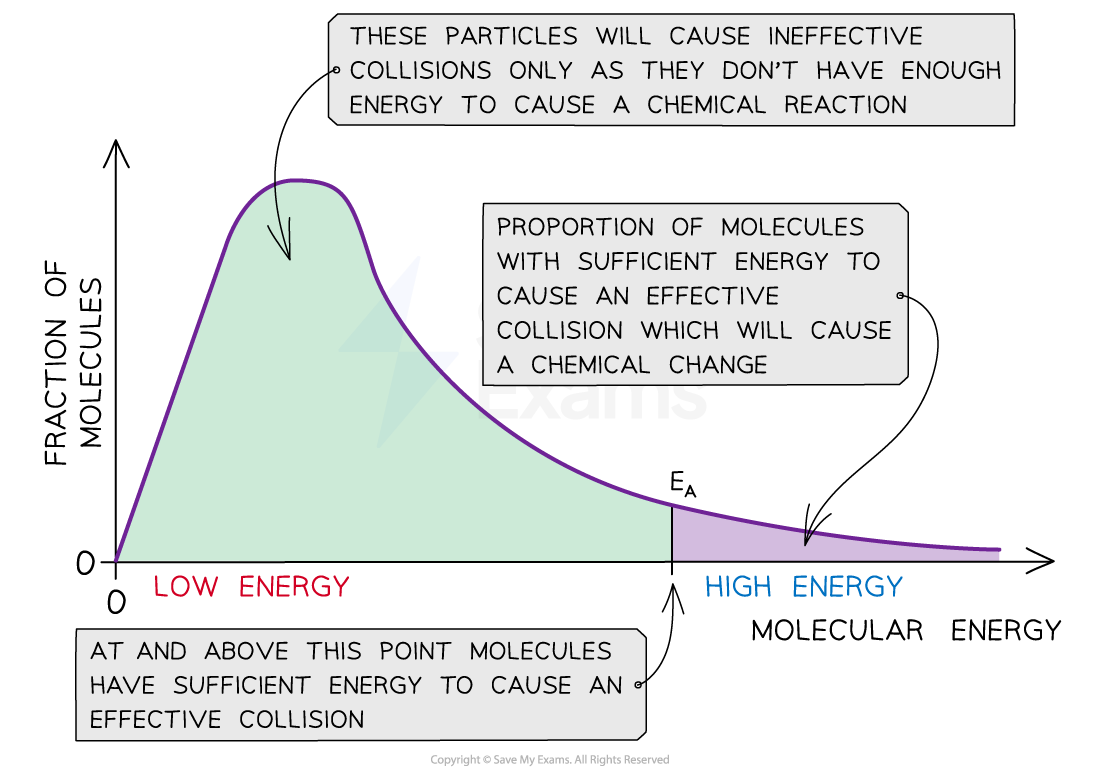
The Maxwell-Boltzmann curve shows the distribution of the energies of colliding particles and the activation energy.

• When the temperature is increased, the distribution curve peak shifts to the right and flattens

• This results from:

  • An increase in the average molecular energies of reacting molecules (peak shifts to the right)

  • An increase in the fraction of these molecules that have energies greater or equal to the activation energy (flattened curve)

  • However, the area under both curves, which represents the total number of particles, remains the same

Temperature Effect on Maxwell-Boltzmann Distribution Curve

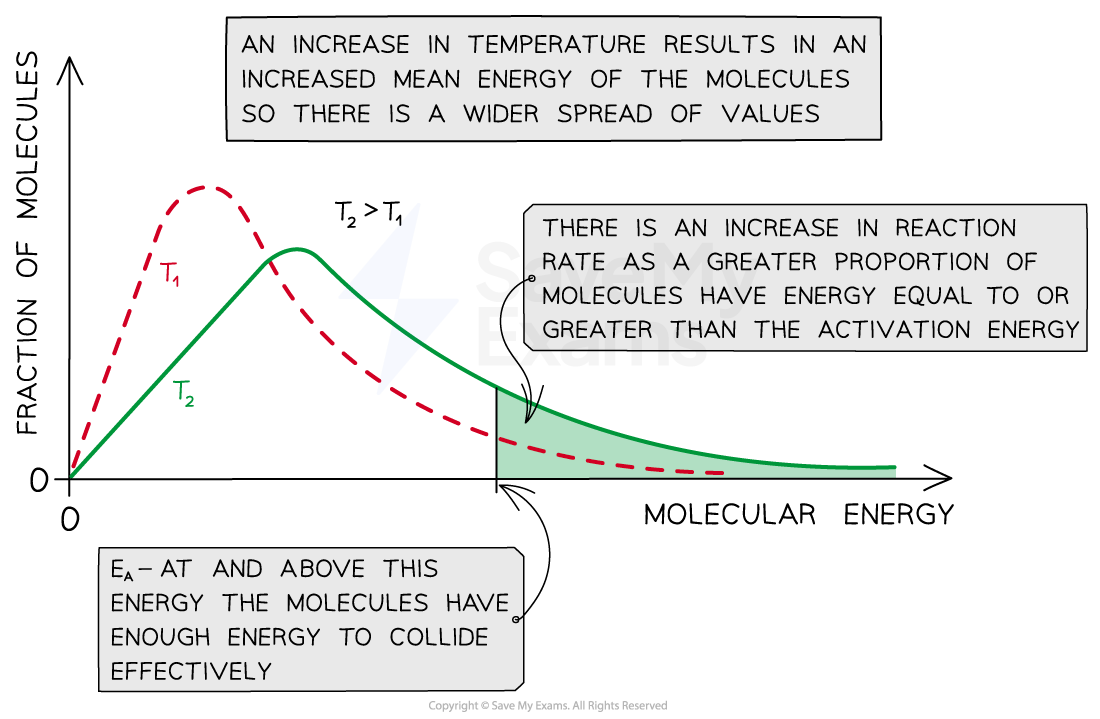
A graph showing the effect of temperature on the kinetic energy of reacting molecules. An increase in temperature increases the fraction of reactant molecules with the required activation energy