Partial Pressure & Total Pressure (College Board AP® Chemistry)
Study Guide
Written by: Oluwapelumi Kolawole
Reviewed by: Stewart Hird
Partial Pressure & Total Pressure
What is Pressure?
Pressure is a measure of the collision of gas particles with the walls of its container
Demonstrating Gas Pressure
Gas particles exert pressure by constant collision with the walls of their container
It is mathematically defined as force per unit area and measured in newtons per meter square (Nm-2)
The pressure exerted by a 1m2 column of air at sea level, referred to as atmospheric pressure, is measured as 1 × 105 Nm-2
The SI unit of atmospheric pressure is the Pascal (Pa):
1 Pa = 1 × 105 Nm-2 = 1 × 102 kPa
Standard atmospheric pressure, often called atmospheric pressure, is the pressure sufficient to support a column of mercury 760 mm high
In SI units, this pressure is given as 1.01325 × 105 Pa
It is also used to define some non-SI units of pressure such as atmosphere (atm) or torr
1 atm = 760 mmHg = 760 torr = 1.01325 × 105 Pa = 101.325 kPa
Dalton’s Law of Partial Pressure
John Dalton while studying the properties of air observed that “the total pressure of a mixture of gases equals the sum of the pressures that each would exert if it were present alone”
For example, the total pressure (PT) exerted by a mixture of gases A, B and C is given by the relationship:
PT = PA + PB + PC where PA, PB, and PC are the partial pressures of the gases A, B and C
This observation is known as Dalton’s Law of Partial Pressure
The partial pressure of a gas is the pressure exerted by the gas in a mixture of gases
Since each gas in a mixture behaves independently, we can relate the amount of a given gas in a mixture to its partial pressure
PA = XA × PT; where XA known as the mole fraction of gas A is a dimensionless number which expresses the ratio of the number of moles of gas A to the total number of moles of the gases in the mixture
XA = nA/(nA + nB + nC)
Partial pressure may also be determined using the volume fraction— the ratio of the volume of gas A to the total volume of the gases in the mixture
Worked Example
A 10.00 L vessel, at 25 ℃, contains the following mixture of the noble gases
0.765 mol helium.
0.330 mol neon.
0.110 mol argon.
Calculate the partial pressure of each of the gases in the mixture.
Calculate the total pressure of the mixture in atm.
Answer:
Step 1: Determine the total number of moles of the gas mixture
nT = nHe + nNe + nAr
nT = 0.765 + 0.330 + 0.110 = 1.205 moles
Step 2: Using the ideal gas equation, find the total pressure of the gas mixture
PT = nTRT/V
Remember: T must be in Kelvin, 25 + 273 = 298 K
R = 0.08206 L.atm mol-1 K-1 since we are asked to determine the pressure in atm
PT = 1.205 × 0.08206 × 298/10.00
PT = 2.95 atm
Step 3: Determine the partial pressure for each gas using its mole fraction and total pressure
Helium
PHe = nHe/nT × PT
PHe = 0.765/1.205 × 2.95
PHe = 1.87 atm
Neon
PNe = nNe/nT × PT
PNe = 0.330/1.205 × 2.95
PNe = 0.807 atm
Argon
PAr = nAr/nT × PT
PAr = 0.110/1.205 × 2.95
PAr = 0.269 atm
Examiner Tips and Tricks
Exam questions will often lay questions out in this order, where:
Part a asks for the partial pressures
Part b asks for the total pressure
You can answer the questions in any order, as shown.
For the worked example above, you have to calculate the total pressure first to be able to calculate the partial pressures
Worked Example
Consider the apparatus shown in the following drawing below
When the valve between the two containers is opened and the gases are allowed to mix, how does the volume occupied by the H2 gas change? What is the partial pressure of H2 after mixing?
How does the volume of the Ne gas change when the gases mix? What is the partial pressure of Ne in the mixture?
What is the total pressure in the container after the gases mix?
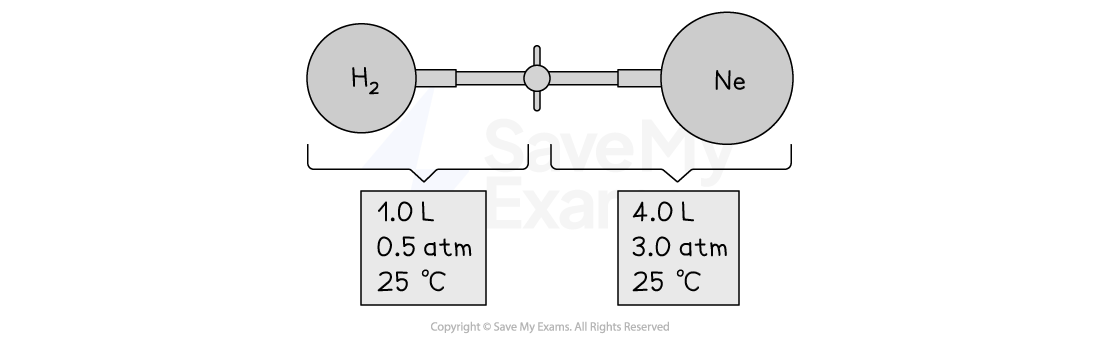
Answer:
Answer 1: The volume of H2 increases from 1 L to 5 L on opening the valve because the particles of the gas spread out.
To calculate the partial pressure of hydrogen:
PH2 = (Volume of H2/Total volume) × Pressure of hydrogen gas
PH2 = ⅕ × 0.5
PH2 = 0.1 atm
Answer 2: The volume of Ne increases from 4 L to 5 L on opening the valve and mixing of the gases.
To calculate the partial pressure of neon:
PNe = (Volume of Ne/Total volume) × Pressure of hydrogen gas
PNe = ⅘ × 3
PNe = 2.4 atm
Answer 3: To calculate the total pressure:
PT = PNe + PH2
PT = 0.1 + 2.4
PT = 2.5 atm
Application of Dalton’s Law in Collection of Gas over Water
A useful application of Dalton’s law of partial pressures arises when gases are collected over water
For example, when potassium chlorate, KClO3 is heated, the oxygen gas produced can be collected over water because it does not react with water and is not appreciably soluble in it
However, the oxygen gas collected in this way is not pure because water vapor is also present
The total gas pressure is equal to the sum of the pressures exerted by the dry oxygen gas and the water vapor:
PT = Pdry O2 + PH2O
This means we must account for the pressure of water when determining the amount of oxygen gas produced
The vapor pressure of water is usually constant at a given temperature
Worked Example
The volume of hydrogen gas collected over water at 30°C and pressure of 988 mmHg when calcium reacts with hydrochloric acid is 641 mL.
What is the mass of hydrogen collected if the vapor pressure of water at 30°C is 31.82 mmHg?
Answer:
Step 1: Determine the pressure of the dry hydrogen gas using Dalton’s Law:
PT = Pdry H2 + PH2O
Pdry H2 = PT - PH2O
Pdry H2 = 988 - 31.82
Pdry H2 = 956.18 mmHg
Step 2: Using the ideal gas equation, determine the number of moles of hydrogen gas produced:
n = PV/RT
P = 956.18 mmHg
V = 641 mL/1000 = 0.641 L
R = 62.36 L.mmHg mol-1 K-1 (R value used because of the units of P and V)
T = 30 + 273 = 303 K
n = 956.18 × 0.641/ 62.36 × 303
n = 0.0324 mole
Step 3: Use number of moles to determine the mass of hydrogen:
n = mass/molar mass
Mass = n × molar mass
Mass = 0.0324 × 2.0 = 0.065 g
Last updated:
You've read 0 of your 5 free study guides this week
Sign up now. It’s free!
Did this page help you?
