Photoelectric Effect (College Board AP® Chemistry)

Photons

• One of the main characteristics of light is its wave-particle duality

• This means that light can behave as a wave, but also as a particle

• As seen in previous sections, a light wave has frequency, wavelength and energy

• However, the discovery of the photoelectric effect suggested that light can also behaves as a particle

• The photoelectric effect was observed when some metals emit electrons when light was shone on them

  • The results of this experiment suggested that light must come into particles

• A light particle is called a photon

Absorption and Emission of photons

• Electrons move around the nucleus of the atoms in energy shells

• Atoms and molecules can absorb photons, and the electrons will jump to higher energy shells

  • When this occurs, the energy of the atom or molecule increases by an amount equal to the energy of the photon

• A moment later, a photon will be emitted, and the electrons will return to their original shell which is also called the ground state

  • When this occurs, the energy of the atom or molecule will decrease by an amount equal to the energy of the photon

Absorption and Emission diagram

The difference between absorption and emission depends on whether electrons are jumping from lower to higher energy levels or the other way around

The Hydrogen Emission Spectrum

• Niels Bohr constructed the hydrogen emission spectrum where he showed the energy released when electrons jump from higher shells to lower shells

• Bohr suggested that electrons can only exist in fixed energy shells

  • This means that electronic transitions can only occur when photons with an specific amount of energy are absorbed or released

• Each electronic transition has to do with photons from specific regions of the electromagnetic spectrum

Regions of the electromagnetic spectrum 

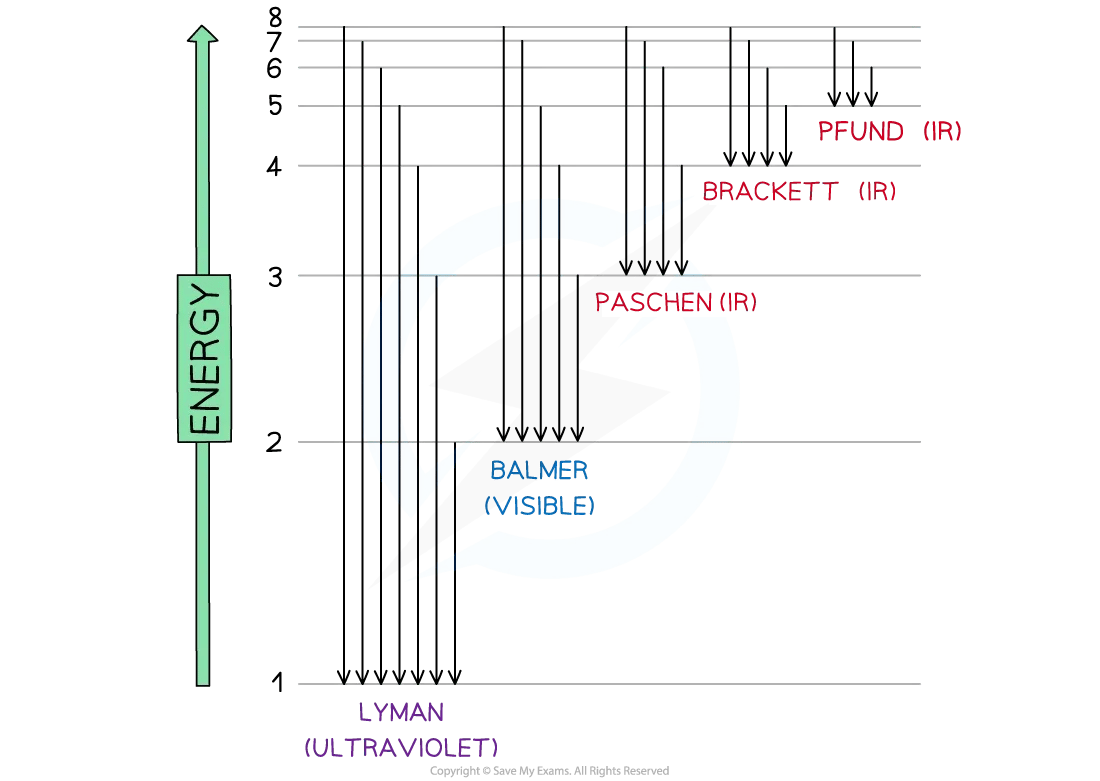
Electron jumps in the hydrogen spectrum

• The jumps can be summarized in table below:

Electron transitions summary

Energy of Photons

Frequency, Wavelength and Energy

• As it was shown in the electromagnetic spectrum, the shorter the frequency of an electromagnetic wave, the longer its wavelength

  • Frequency (ν) and wavelength (λ) are inversely proportional

  • The equation that links them is:

• In this equation c is the speed of light which is 2.998 x 10⁸ ms^-1

• The spectrum also shows that, the shorter the frequency, the lower the energy of the radiation

  • Frequency (ν) and energy (E) are directly proportional

  • The equation that links the energy emitted or absorbed by a photon and its frequency is:
                                                    

  • In this equation h is the Planck’s constant, which is 6.626 x 10^-34 J s

• These two equations can be used to calculate frequency, wavelength or energy when one of them is given