Graphical Representations of the Gas Laws (College Board AP® Chemistry): Study Guide
Graphical Representations of the Gas Laws
The relationship between any two of the variables which describe the properties of an ideal gas can be established by keeping the other variables constant
These variables are:
Pressure
Volume
Temperature
Amount of gas (moles)
These relationships expressed mathematically and graphically are known as Gas Laws
Pressure-Volume Relationship: Boyle’s Law
This relationship was first investigated by the British chemist, Robert Boyle, using a J-tube, showing that the volume of gas decreased as the pressure increased
This observation is summarized by the statement by Boyle’s Law which states that: the volume of a fixed amount of gas at constant temperature is inversely proportional to the pressure:
V ∝ 1/P ; PV = constant
Simplifying the mathematical equation gives Boyle’s equation:
P1V1 = P2V2
Pressure-Volume Relationship
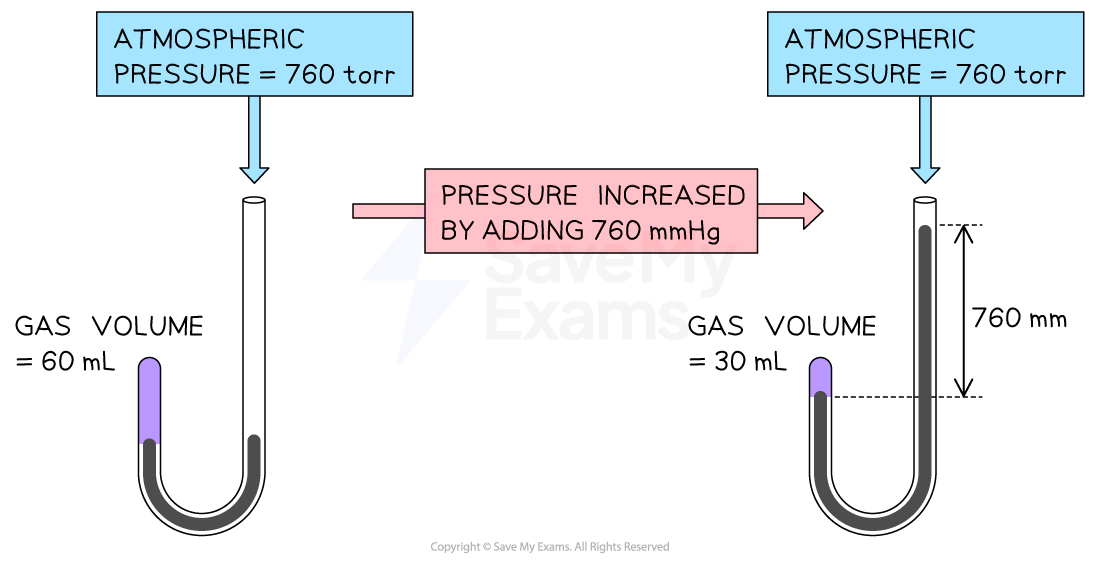
Boyle’s experiment uses a J-tube to demonstrate the volume-pressure relationship of a gas. Gas volume decreases on increasing the pressure in the tube
This relationship can also be visualized using two graphs:
A plot of V against P gives a curve for a given quantity of gas at a fixed temperature
A straight line is obtained when V is plotted against 1/P or P against 1/V
Graphical Representation of Pressure-Volume Relationship

Graphical representations of Boyle’s Law
Temperature-Volume Relationship: Charles’s Law
The earliest investigator of the effect of temperature on volume was French scientist, Jacques Charles
He observed that at constant pressure, the volume of a gas sample expands when heated and contracts when cooled
At any given pressure, the plot of volume versus temperature yields a straight line
By extrapolating the line to zero volume, we find the intercept on the temperature axis to be -273.15 ℃
Temperature-Volume Relationship on Celsius Scale
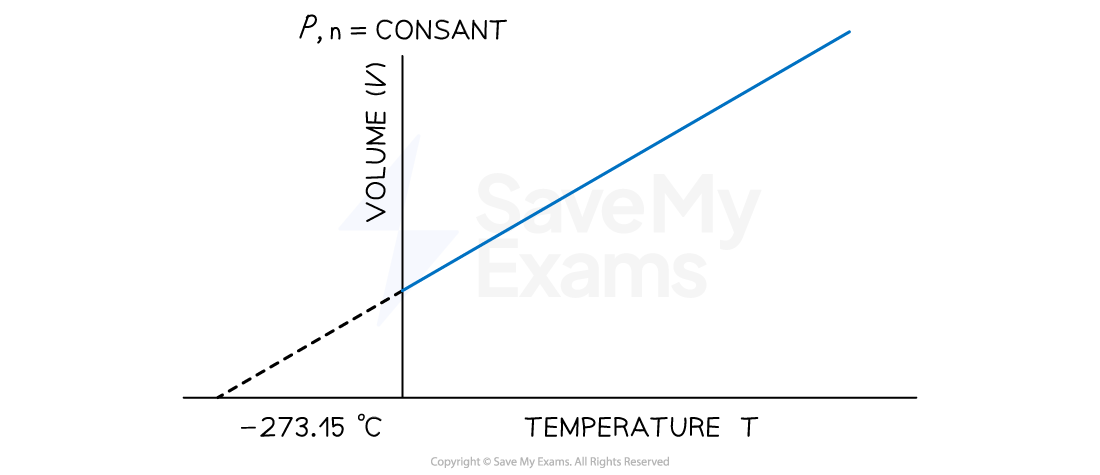
A graph showing the linear relationship between temperature (in degrees Celsius) and volume. The line intercepts the temperature axis at a value of 273.15 ℃
This implies that at a temperature of 273.15 ℃, the volume of a substance, if it remains gaseous will be zero
However, this could not happen, given that gases liquefy before this temperature, and the relationship does not apply to liquids
Kelvin Temperature Scale
In 1848, British physicist William Thomson, whose title was Lord Kelvin, realized the significance of the volume-temperature relationship using the Celsius temperature scale
He identified the lowest possible temperature as absolute zero
He then set up an absolute temperature scale, now called the Kelvin temperature scale (K) with absolute zero as the starting point
On the absolute temperature scale, 0 K is equivalent to -273.15 ℃
In terms of the Kelvin scale, the temperature-volume relationship known as Charles’s Law can be stated as: the volume of a fixed amount of gas maintained at constant pressure is directly proportional to its absolute temperature:
V ∝ T or V/T = constant
Simplifying the relationship gives:
V1/T1 = V2/T2
A plot of volume against temperature in Kelvin also gives a straight line which intercepts the volume and temperature axis at zero
Temperature-Volume Relationship on the Kelvin Scale

A graph showing the linear relationship between absolute temperature and volume. The line intercepts the temperature axis at a value of 0 K
Quantity-Volume Relationship: Avogadro’s Law
The relationship between the amount in moles of a gas and its volume follows from the work of Joseph Louis Gay-Lussac and Amedeo Avogadro
Gay-Lussac observed that at a given pressure and temperature, the volumes of gases that react with one another are in the ratios of small whole numbers
For example, two volumes of hydrogen gas react with one volume of oxygen gas to form two volumes of water vapor:
2H2 (g) + O2 (g) → 2H2O (g)
A few years later, Amedeo Avogadro interpreted Gay-Lussac’s observation by proposing an important hypothesis which set the foundation for demonstrating the mole-volume relationship and Avogadro’s Law
The hypothesis states that: Equal volumes of gases at the same temperature and pressure contain equal numbers of molecules
For example, at 0 ℃ and 1 atm, 22.4 L of a gas contains 6.022 × 1023 gas molecule which is equivalent to one mole
Avogadro’s law follows from this hypothesis: the volume of a gas maintained at constant temperature and pressure is directly proportional to the number of moles of the gas:
V ∝ n ; V/n = constant
Simplifying the relationship gives:
V1/n1 = V2/n2
Quantity-Volume Relationship

Graphical representation of Avogadro’s Law
Worked Example
A chemical reaction produced 4.38 mL of hydrogen gas at 19 ℃ and 200 kPa pressure.
What volume of the gas would be produced at 25℃ at the same pressure?
Answer:
Analyze: From the question, the following parameters were provided
V1 = 4.38 mL
T1 = 19 ℃
T2 = 25 ℃
P = 200 kPa
We are then asked to calculate the final volume while pressure is kept constant
Plan: Since the pressure remains constant, the problem requires the use of the volume-temperature relationship expressed by Charles’s equation
Solution:
Step 1: Convert temperature values in ℃ to K:
T1 = 19 + 273 = 292 K
T2 = 25 + 273 = 298 K
Step 2: Rearrange Charles’s equation in terms of the final volume V2 and solve for V2:
V2 = V1 × T2 / T1
V2 = 4.38 × 298 / 292
V2 = 4.47 mL
Worked Example
In a reaction involving the decomposition of limestone, CaCO3, 20.0L of CO2 at 23 ℃ and 1.00 atm were collected.
What would be the volume of CO2 collected if the pressure were halved at the same temperature?
Answer:
Analyze: We have the following parameters from the question:
P1 = 1.00 atm
V1 = 20.0 L
P2 = ½ P1 = 0.500 atm
T = 23 ℃
We are then asked to calculate the final volume while the temperature is kept constant
Plan: Since temperature is kept constant, the volume-pressure relationship using Boyle’s equation would be required to determine the new volume
Solution: Rearrange the Boyle’s equation in terms of V2 and solve for V2:
V2 = P1 × V1 / P2
V2 = 1.00 × 20.0/ 0.5
V2 = 40.0 L
Worked Example
Sodium reacts with water at 25.0 ℃ to produce hydrogen gas. The equation of the reaction is given as follows:
2Na (s) + 2H2O (l) → 2NaOH (aq) + H2 (g)
246 mL of hydrogen gas is collected over water at 25.0 ℃ and 1.00 atm.
Calculate the mass of sodium used in the reaction. Vapor pressure of water at 25.0 °C is 0.0313 atm
Answer:
Analyze: This problem requires the application of stoichiometry, Dalton’s Law of partial pressure and the ideal gas equation.
Plan:
Determine the pressure of the dry hydrogen gas produced, using Dalton's partial pressure equation
Use the ideal gas equation to determine the number of moles of hydrogen obtained
Use the stoichiometric ratio from the balanced chemical equation to determine the number of moles of sodium which must have reacted
Convert the number of moles of sodium to the mass of sodium
Solution
Step 1: Determine the pressure of the dry hydrogen gas produced:
PH2 = Ptotat - PH2O
PH2 = 1.00 - 0.0313
PH2 = 0.9687 atm
Step 2: Determine the number of moles of hydrogen gas using the ideal gas equation:
PV = nH2RT
PH2 = 0.9687 atm
VH2 = 246 mL/ 1000 = 0.246 L
Remember: Volume must be in L
R = 0.08206 L.atm mol-1 K-1
T = 25 + 273 = 298 K
Remember: Temperature must be in K
nH2 = ?
nH2 = PV/RT
nH2 = 0.9687 × 0.246 / 0.08206 × 298
nH2 = 0.00974 mole
Step 3: Determine the number of moles of sodium required given a 2:1 ratio from the balanced chemical equation
nNa = 2 × nH2
nNa = 2 × 0.00974
nNa = 0.0195 mole
Step 4: Convert number of moles determined in step 3 to mass of sodium by multiplying moles by the molar mass of sodium:
MNa = nNa × MrNa
MNa = 0.0195 × 22.99
MNa = 0.45 g

Unlock more, it's free!
Did this page help you?