Resources & Population Density (College Board AP® Biology)

Effect of Density on Populations

The Logistic Growth Model

• The exponential growth model assumes unrestricted growth in the population

• An unrestricted scenario is unlikely in nature and so populations rarely follow the J-curve for exponential growth

• Instead, populations are impacted by

  • Density-dependent factors - These are factors which exert a stronger effect as the population increases e.g. competition for resources, predation and disease

  • Density-independent factors - These are factors which restrict growth regardless of size or density e.g. natural disasters, extreme weather events or habitat destruction

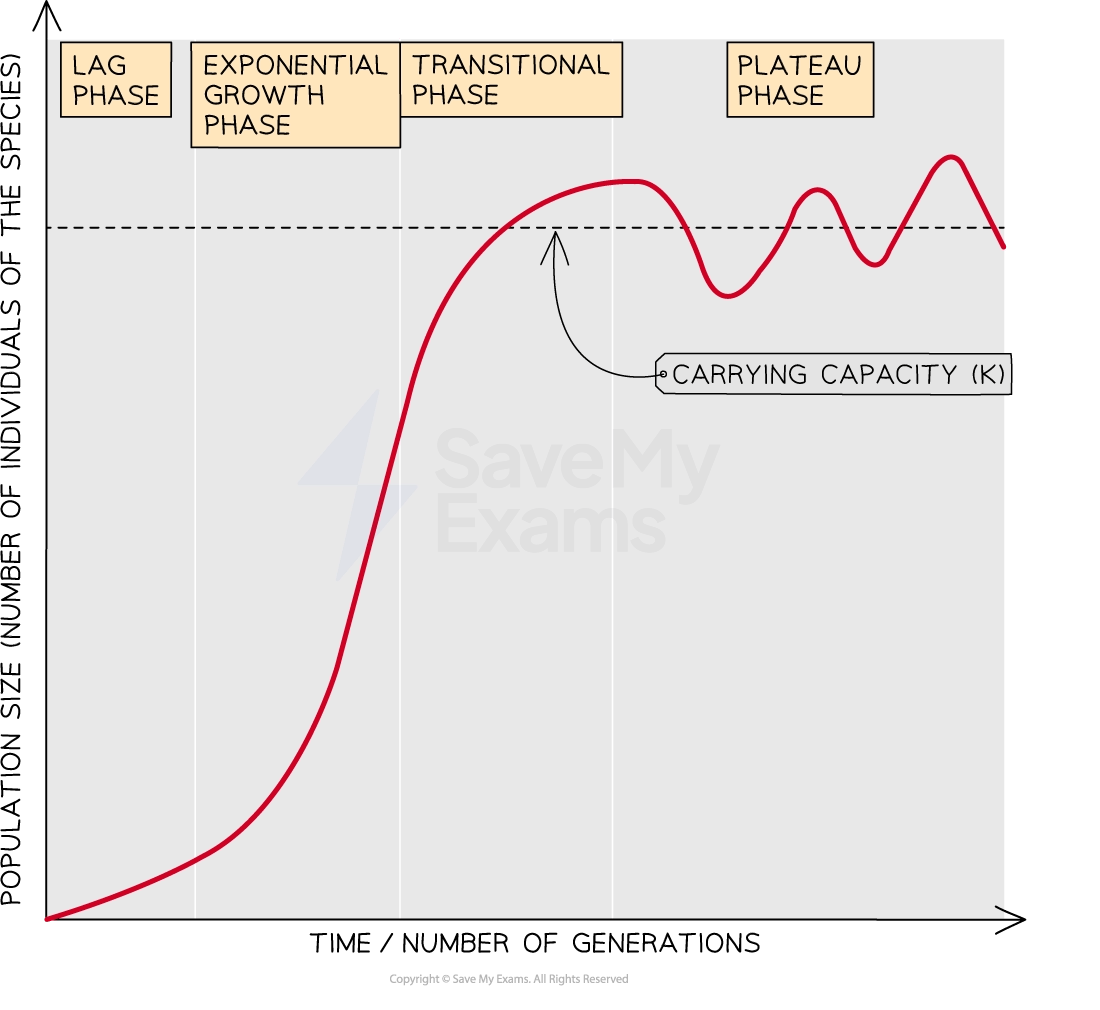
• The logistic model produces a population growth curve which is sigmoid, or S shaped

• Such curves contain three phases:

  • Exponential phase

    • Also known as the logarithmic phase

    • Here there are no factors that limit population growth, so the population increases exponentially

    • The number of individuals increases, and so does the rate of growth

    • This part of the curve is J shaped

  • Transition phase

    • As the population size increases, the density may increase past the threshold that can be supported by the system resource availability

    • Limiting factors start to act on the population, eg. competition increases and predators are attracted to large prey populations

    • The rate of growth slows, though the population is still increasing

  • Plateau phase

    • Also known as the stationary phase

    • Limiting factors cause the death rate to equal the birth rate and population growth stops

    • This plateau occurs at the carrying capacity

    • The population size often fluctuates slightly around the carrying capacity

Population Growth Curve Graph

Sigmoidal population growth curves show an exponential (J-shaped) growth phase, a transitional phase and a plateau phase

• As limits to growth are imposed upon a population (as density changes), a new mathematical model emerges:

where:

dt = change in time
N = population size
r_max = maximum per capita growth rate of the population
K = carrying capacity

• The essence of this equation is that when N is large (near to the carrying capacity), then the term in brackets will be close to zero, so the growth rate will be small

An Example of a Logistic Growth Model

• Population growth curves can generally be seen in any newly established or recovering population, eg.

  • Antarctic fur seals were hunted extensively during the 1800s and underwent a population recovery following the end of this practice

  • The recovery of the seal population in some locations follows a classic growth curve, eg. in the graph below for seals on Cape Shirreff, Antarctica

    • Pup count is used to represent the size of the seal population

  • Note that this recovery has not continued throughout the early 21st century, with climate change having since caused severe declines in many seal populations

Antarctic Fur Seal Population Growth Curve Graph

The Antarctic fur seal population in Cape Shirreff, Antarctica, followed a classic growth curve between 1960 and the early 2000s

Exponential Population Growth

Testing for exponential growth with a logarithmic scale

• Population growth is exponential when the speed of growth is proportional to the number of individuals, ie. a population of 20 individuals will reproduce at twice the rate of a population of 10 individuals

• It is possible to assess whether or not exponential growth is occurring by plotting population size (y) against time (x) on a graph with a logarithmic scale on the y axis and a nonlogarithmic scale on the x axis

  • Logarithmic scales can be very useful when investigating factors that vary over several orders of magnitude, eg. population size

    • 'Orders of magnitude' refers to whether values are measured in, e.g. tens, hundreds, thousands etc.; using a log scale allows tens and millions to be represented on the same easily visible scale

  • The numbers in a logarithmic scale represents logarithms, or powers, of a base number

  • If using a log₁₀ scale, in which the base number is 10, the numbers on the y axis represent a power of 10, e.g. 1=10¹ (10), 2=10² (100), 3=10³ (1000) etc.

  • Logarithmic scales allow for a wide range of values to be displayed on a single graph

• An exponentially growing population plotted with a log scale on the y axis will appear as a straight line:

Exponential Population Growth on a Logarithmic Scale Graph

An exponentially growing population plotted with a log scale on the y-axis will appear as a straight line