Population Ecology (College Board AP® Biology) : Study Guide

Population growth

• A population can be defined as:

a group of organisms of the same species, occupying a particular space at a particular time

• Population dynamics are the changes in population size, structure and composition over time

• Populations are influenced by interactions among individuals, their environment, and the availability of energy and resources

• The growth or decline of a population depends on biotic factors and abiotic factors

• Population growth is described using the equation:

• Where:

  • N is population size

  • dN/dt is the change in population size over time

  • B is the birth rate

  • D is the death rate

• Exponential growth occurs when reproduction is unconstrained, following the equation:

  

  • Where:

    • dt = change in time

    • N = population size

    • r_max = maximum per capita growth rate of a population

• This growth creates a J-shaped curve, characteristic of exponential growth

Population density

• Various constraints impact population growth:

  • Density-dependent factors are factors that have a stronger effect as population density increases

    • E.g. competition for resources, predation, disease

  • Density-independent factors affect populations regardless of population density

    • E.g. natural disasters, extreme weather

The logistic growth model

• When density-dependent and density-independent factors limit population growth, logistic growth usually occurs

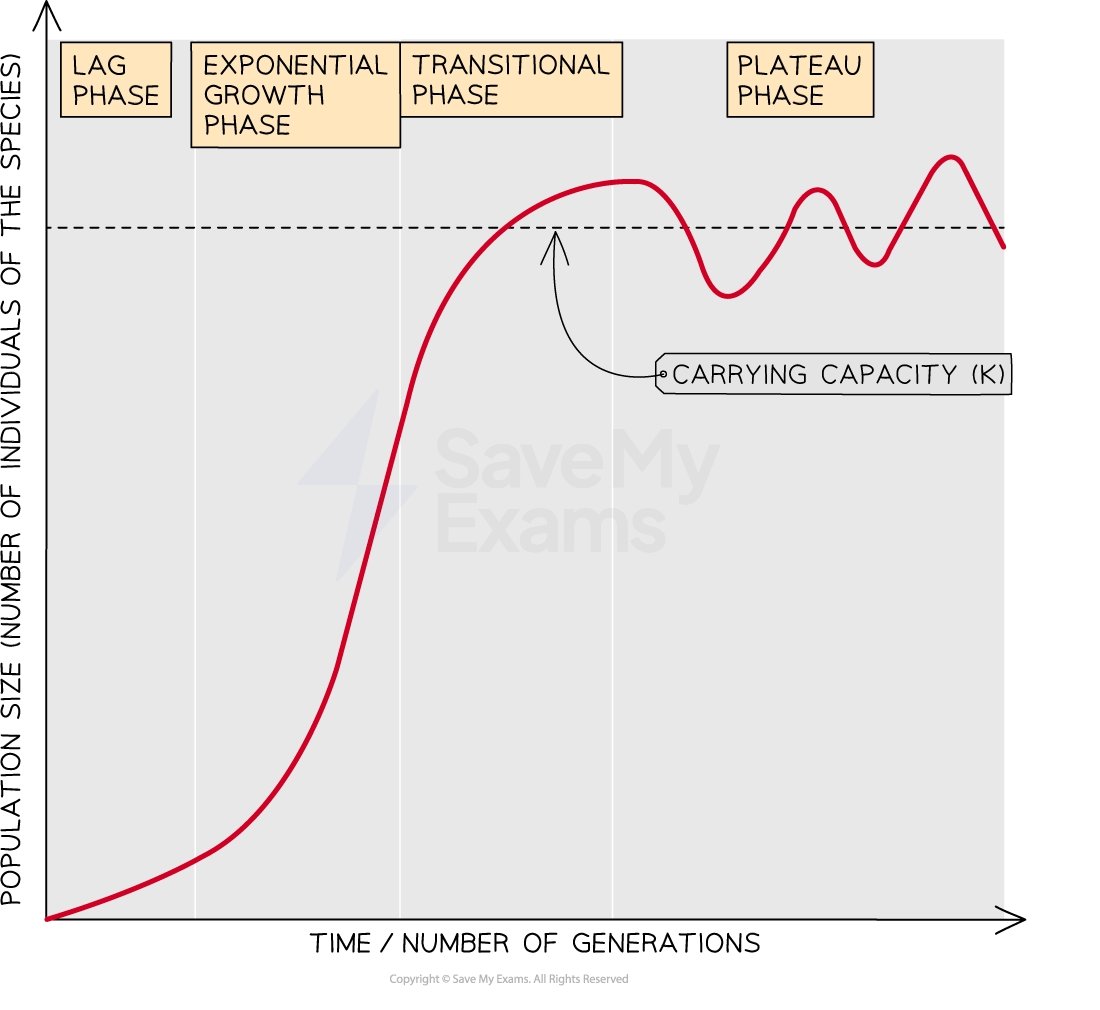
• The logistic model produces a population growth curve which is sigmoid, or S-shaped

• Such curves contain four phases:

  • lag phase

    • The initial stage of population growth

    • Characterized by slow growth and a small population size

    • Organisms are adapting to their environment with low levels of reproduction

  • exponential phase

    • Also known as the logarithmic phase

    • Here there are no factors that limit population growth, so the population increases exponentially

    • The number of individuals increases, and so does the rate of growth

    • This part of the curve is J-shaped

  • transition phase

    • As the population size increases, the density may increase past the threshold that can be supported by the system resource availability

    • Limiting factors start to act on the population, eg. competition increases and predators are attracted to large prey populations

    • The rate of growth slows, though the population is still increasing

  • plateau phase

    • Also known as the stationary phase

    • Limiting factors cause the death rate to equal the birth rate and population growth stops

    • This plateau occurs at the carrying capacity where the environment cannot sustain any further increase in population

    • The population size often fluctuates slightly around the carrying capacity

Equation for the logistic growth model

• The logistic growth model is described by the following equation:

• Where:

  • dt is the change in time

  • N the population size

  • r_max is the maximum per capita growth rate of the population

  • K is the carrying capacity

• The essence of this equation is that when N is large (near to the carrying capacity), then the term in brackets will be close to zero, so the growth rate will be small