Cells & Surface Area (College Board AP® Biology): Study Guide

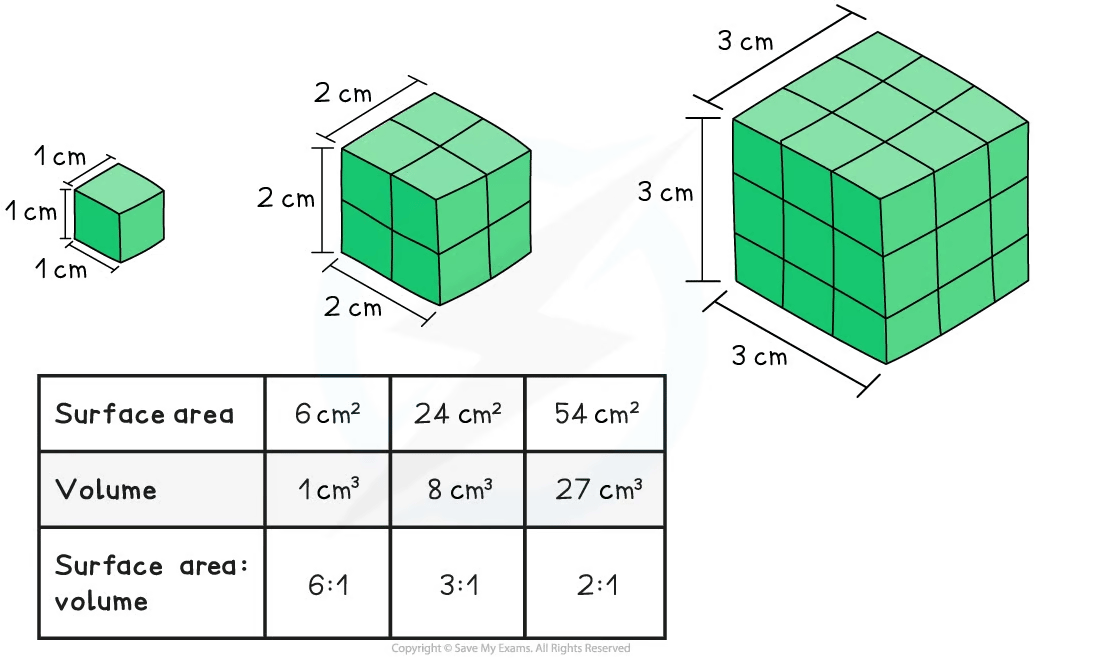
Surface area-to-volume ratio

• Surface area and volume are both very important factors in the exchange of materials in organisms

  • Surface area refers to the total area of the organism that is exposed to the external environment

  • Volume refers to the total internal volume of the organism (total amount of space inside the organism)

• As the surface area and volume of an organism increase (and therefore the overall "size" of the organism increases), the surface area : volume ratio decreases

• This is because volume increases much more rapidly than surface area as size increases

Importance of surface area-to-volume ratios

• Having a high surface area-to-volume ratio increases the ability of a biological system to perform the following important functions

  • obtaining necessary resources e.g. oxygen, glucose, amino acids

  • eliminating waste products e.g. carbon dioxide, urea

  • acquiring or dissipating thermal energy (heat)

  • exchanging chemicals and energy with the surroundings e.g. absorbing hormones at the cell surface in the hormone's target organ

Calculating surface area-to-volume ratios

	Sphere	Cube	Rectangular Solid	Cylinder
Surface Area		6s2	2lh + 2lw + 2wh
Volume		s3	l × w × h
Example	If r = 1 cm SA = 4π(1)2 = 4π cm2 V = 4/3 πr3 = 4/3 π13 =  4/3 π  ∴ SA:V ratio = 4:4/3 = 3:1	If s = 1 cm then SA = (1×1)×6 SA = 6cm2 V = s3 = 13 =1cm3 ∴ SA:V ratio = 6:1	If l = 4cm, w = 2cm, h = 1cm, then SA = 2((4×1)+(4×2)+(2×1)) = 28cm2 V = 4 × 2 × 1 = 8cm3 ∴ SA:V ratio = 28:8 = 3.5:1	If r = 2 cm and h = 6cm, then SA = 2πrh + 2πr2 = 8π +24π = 32π cm2 V = π(2)2 × 6 = 24π cm2 ∴ SA : V ratio = 32 : 24 = 1.33:1

The surface area:volume ratio calculation differs for different shapes (these shapes can reflect different cells or organisms)

Maximizing surface area-to-volume ratio

• As organisms increase in size, their surface area to volume ratio decreases

  • Small cells have a high surface area-to-volume ratio and more efficient exchange of materials with the environment

  • Larger cells have a lower surface area-to-volume ratio and are less efficient at exchanging materials with their environment

  • Materials exchanged include

    • oxygen

    • carbon dioxide

    • water

    • heat exchange

• Some single-celled organisms can rely on simple diffusion alone to exchange materials with their environment

• More complex cellular structures (e.g. membrane folds) are necessary to exchange materials with the environment adequately

• As organisms evolved from single-celled to multicellular, more sophisticated exchange systems (e.g. lungs) evolved to maintain diffusion rates that were high enough to sustain life

Examples of exchange structures

• Exchange structures may evolve to be specially adapted to maximize exchange

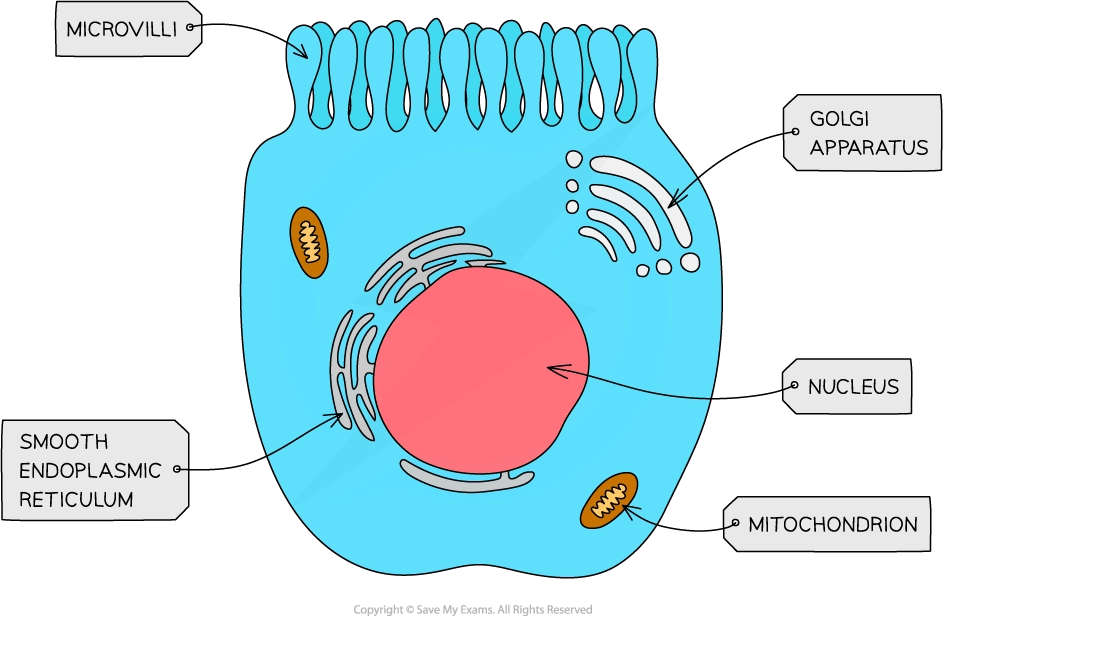
Gut epithelial cells

• A cell on the inside surface of the small intestine is in contact with the flow of food passing through the lumen of the intestine

• The cell's principal role is to absorb important nutrient molecules for distribution around the rest of the organism's body

• Only one surface of the cell is in contact with the food flow; this is the upper surface as shown

  • The remaining surfaces of the cell are in direct contact with other cells in the tissue, so cannot absorb food molecules directly from the lumen

• So the surface area of the food-contacting surface is maximized by folded structures called microvilli

• These increase the internal surface area of the small intestine by a factor of around 100

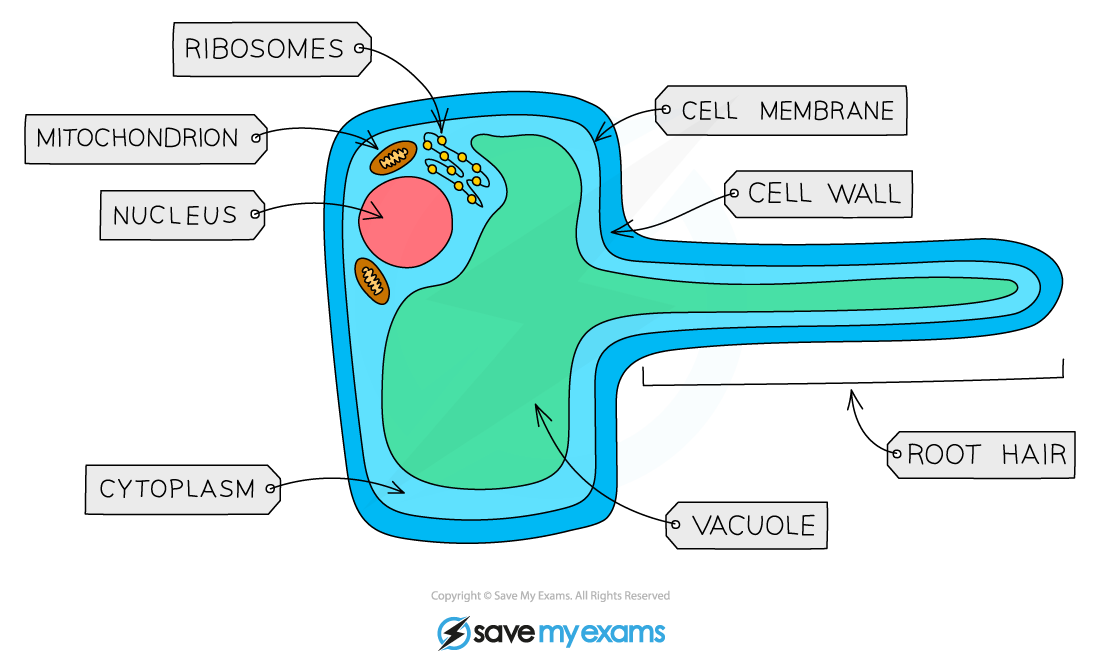
Root hair cells

• Root hairs are single-celled extensions of epidermis cells in the root

  • They grow between soil particles and absorb water and minerals from the soil

• Root hair cells are adapted for the efficient uptake of water (by osmosis) and mineral ions (by active transport)

  • Root hairs increase the surface area of plant roots, increasing the rate at which water and minerals can be absorbed

Guard cells

• Guard cells surround stomata on the lower surface of a leaf; their role is to expand and contract which opens and closes the stomata allowing for gas exchange

• The surface area-to-volume ratio of guard cells changes as they expand and contract

• As guard cells become turgid, they curve outward which creates a larger stomatal opening

  • This increases the effective surface area for gas exchange

• The small size of guard cells relative to the open stomata ensures efficient diffusion of gases, as the surface area-to-volume ratio is high for the pore area