Revision NotesExam QuestionsPast Papers
A LevelPhysicsOCRExam Questions6. Particles & Medical PhysicsRadioactivity

Radioactivity (OCR A Level Physics)

Exam Questions

35 mins7 questions

Select a question set to download for
Radioactivity

Select an answer set to view for
Radioactivity

Medium
Hard
1a3 marks

An isotope of polonium-213 (Po presubscript 84 presuperscript 213) first decays into an isotope of lead-209 (Pb presubscript 82 presuperscript 209) and this lead isotope then decays into the stable isotope of bismuth (Bi). Fig. 24 shows two arrows on a neutron number N against proton number Z chart to illustrate these two decays.

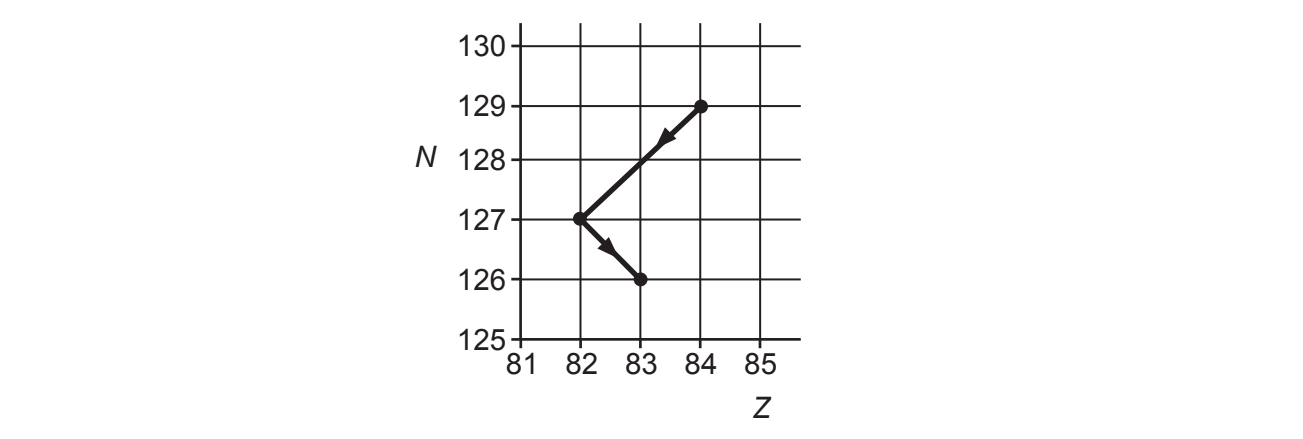
q24-paper-2-june-2018-ocr-a-level-physics

Fig. 24

Complete the nuclear decay equations for

i) the polonium isotope Po presubscript 84 presuperscript 213 space rightwards arrow space Pb presubscript 82 presuperscript 209 space plus space.....................

[1]

 

ii) the lead isotope

Pb presubscript 82 presuperscript 209 space rightwards arrow space Bi presubscript 83 presuperscript..... end presuperscript space plus space straight e presubscript negative 1 end presubscript presuperscript 0 space plus space.....................

 [2]

How did you do?

1b6 marks

A pure sample of polonium-213 is being produced in a research laboratory. The half-life of  Po presubscript 84 presuperscript 213 is very small compared with the half-life of Pb presubscript 82 presuperscript 209.

After a very short time, the ionising radiation detected from the sample is mainly from the beta-minus decay of the lead-209 nuclei.

i) Briefly describe and explain an experiment that can be carried out to confirm the beta-minus radiation emitted from the lead nuclei.

 [2]

ii) The activity of the sample of Pb presubscript 82 presuperscript 209 after 7.0 hours is 12 kBq.

The half-life of Pb presubscript 82 presuperscript 209 is 3.3 hours.

Calculate the initial number of lead-209 nuclei in this sample.

number of nuclei = ......................................................... [4]

How did you do?

Did this page help you?

2a3 marks

Fig. 20 illustrates a device used to determine the relative abundance of charged rubidium ions.

q20-paper-2-june-2019-ocr-a-level-physics

Fig. 20

A uniform magnetic field is applied to an evacuated chamber. The direction of the magnetic field is perpendicular to the plane of the paper.

A beam of positive rubidium ions enters the chamber through a hole at H. The ions travel in a semi-circular path in the magnetic field. The ions are detected at point D.

Each rubidium ion has charge +1.6 × 10–19 C and speed 4.8 × 104 ms–1. The radius of the semi-circular path of the ions is 0.18 m. The mass of a rubidium ion is 1.4 × 10–25 kg.

Calculate the magnitude of the magnetic flux density B of the magnetic field.

B = ........................................... T [3]

How did you do?

2b4 marks

The chemical composition of ancient rocks found on the Earth can be used to estimate the age of the Earth. Nuclei of rubidium-87 (Rb presubscript 37 presuperscript 87) decay spontaneously into nuclei of strontium-87 (Sr presubscript 38 presuperscript 87).

The half-life of rubidium-87 is 49 billion years.

i) Name the two leptons emitted in the decay of a rubidium-87 nucleus.

[1]

ii) The percentage of rubidium left in a sample of an ancient rock is 95%. Estimate the age of the Earth in billion years.

age = ........................... billion years [3]

How did you do?

Did this page help you?

1a3 marks

Co presubscript 27 presuperscript 60  is produced by irradiating the stable isotope Co presubscript 27 presuperscript 59 with neutrons.

Each nucleus of Co presubscript 27 presuperscript 60   then decays into a nucleus of nickel (Ni) by the emission of a low energy beta-minus particle, one other particle and two gamma photons.

Complete the nuclear equations for these two processes.

 Co presubscript 27 presuperscript 59 space plus straight n presubscript midline horizontal ellipsis midline horizontal ellipsis end presubscript presuperscript midline horizontal ellipsis midline horizontal ellipsis end presuperscript space rightwards arrow space Co presubscript 27 presuperscript 60 space rightwards arrow space Ni presubscript midline horizontal ellipsis midline horizontal ellipsis end presubscript presuperscript midline horizontal ellipsis midline horizontal ellipsis end presuperscript space plus space straight e presubscript midline horizontal ellipsis midline horizontal ellipsis end presubscript presuperscript midline horizontal ellipsis midline horizontal ellipsis end presuperscript space plus space midline horizontal ellipsis midline horizontal ellipsis midline horizontal ellipsis space plus space 2 straight gamma

[3]

How did you do?

1b12 marks

Students want to carry out an investigation into gamma photon absorption using a source of Co presubscript 27 presuperscript 60. They add sheets of lead between the source S and a radiation detector T, to give a total thickness d of lead. S and T remain in fixed positions, as shown in Fig. 2.1.

q2b-paper-3-june-2019-ocr-a-level-physics

Fig. 2.1

i) The Co presubscript 27 presuperscript 60   source emits beta radiation as well as gamma radiation. Explain why this would not affect the experiment.

[1]

ii) The students record the number N of gamma photons detected by T in 10 minutes for each different thickness d of lead. The background count is negligible.

The results are shown in a table. The table includes values of ln N, including the absolute uncertainties.

N

d/mm

ln N

4300 ± 440

0

8.37 ± 0.10

2500 ± 250

10

7.82 ± 0.10

1400 ± 150

20

7.24 ± 0.11

800 ± 90

30

6.68 ± 0.11

500 ± 60

40

6.21 ± 0.12

300 ± 40

50

 

N and d are related by the equation N = N0 e–μd where N0 and μ are constants.

1. The students decide to plot a graph of ln N against d. Show that this should give a straight line with gradient    = – μ and y-intercept = ln N0.

[1]

2. Complete the missing value of ln N in the table, including the absolute uncertainty. Show your calculation of the absolute uncertainty in the space below.

[2]

3. In Fig. 2.2, five of the data points have been plotted, including error bars for ln N. Plot the missing data point and error bar. Draw a straight line of best fit and one of worst fit.

[2]

q2-3-paper-3-june-2019-ocr-a-level-physics

Fig. 2.2

4. Use Fig. 2.2 to determine the value of μ in m–1, including the absolute uncertainty.

μ = ...................... ± ...................... m–1 [4]

5. Determine the thickness, d1⁄2, of lead which halves the number of gamma photons reaching T.

d1⁄2 = ........................................ m [2]

How did you do?

Did this page help you?