A LevelPhysicsOCRExam Questions5. Newtonian World & Astrophysics5.6 Damping

Damping (OCR A Level Physics)

Exam Questions

32 mins10 questions

Select a question set to download for
5.6 Damping

Select an answer set to view for
5.6 Damping

Medium
Hard
1a5 marks

A mass hanging from a vertical spring is pulled down.
It is then released from rest at time t = 0.
The mass oscillates vertically in a vacuum with simple harmonic motion about the equilibrium position. The spring is in tension at all times.

Fig. 18.1 shows the position of the mass at t = 0.

q18-paper-1-june-2019-ocr-a-level-physics

Fig. 18.1

At time t = 6.5 s the magnitude of the acceleration a of the mass is 3.6 ms–2 and its displacement x is 4.6 × 10−2 m.

a)
i)
Use the defining equation for simple harmonic motion to show that the natural frequency f0 of the mass-spring system is about 1.4 Hz.

[3]

ii)
Calculate the amplitude A of the oscillations.

A = ........................................ m  [2]

How did you do?

1b4 marks
b)
The mass-spring system shown in Fig. 18.1 is now made to oscillate in air.

Different types of energy are involved in the oscillations of this mass-spring system.

Describe the energy changes that will take place as the mass moves from the lowest point in its motion through the equilibrium position to the highest point in its motion.
[4]

How did you do?

1c5 marks
c)
Fig. 18.2 shows the mass and spring now attached to a mechanical vibrator, which can oscillate with variable frequency.

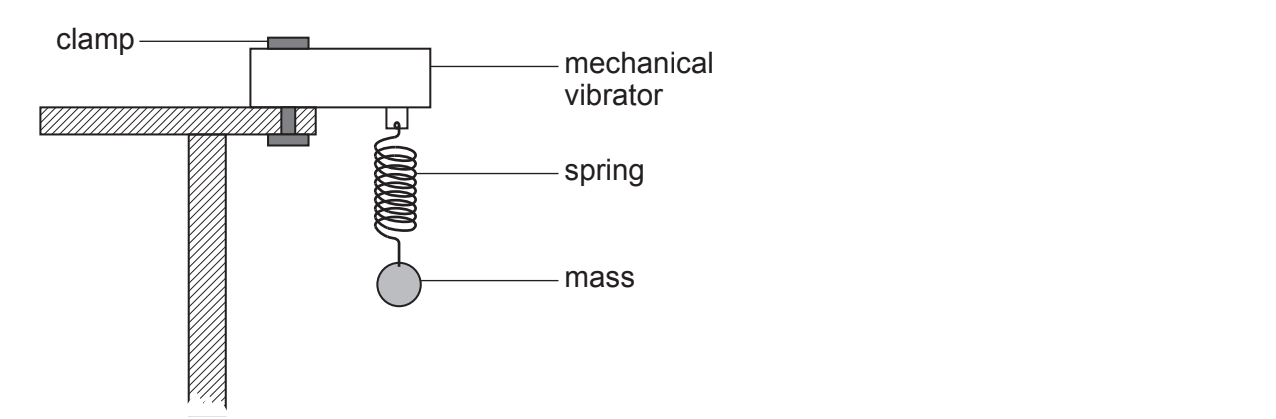
q18c-paper-1-june-2019-ocr-a-level-physics

Fig. 18.2

The mass oscillates in air.

i)
The vibrator frequency is varied from 0 Hz to 2.5 Hz.
On Fig. 18.3, sketch a graph to show the variation with vibrator frequency of the amplitude of the mass. Label your graph K.

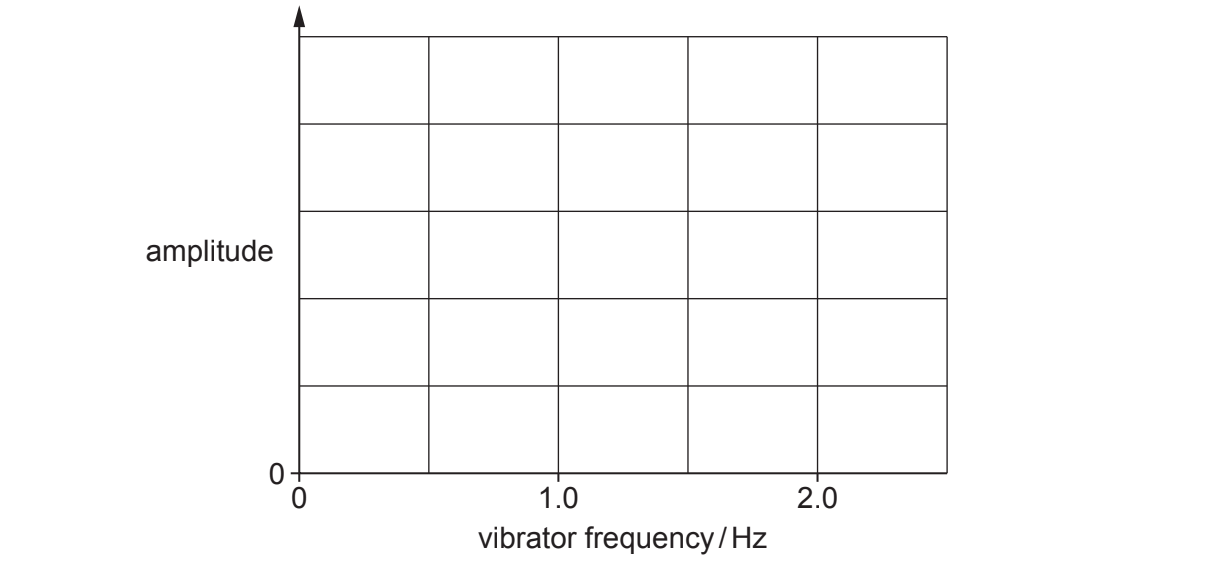
q18ci-paper-1-june-2019-ocr-a-level-physics

Fig. 18.3

[2]

ii)
A light disc is now attached to the mass to increase the damping.
The vibrator frequency is again varied from 0 Hz to 2.5 Hz.
Sketch a second graph on Fig. 18.3 to show the new variation of the amplitude.
Label this graph D.

[1]

iii)
Explain why the phenomenon demonstrated in this experiment can cause problems for engineers when designing suspended footbridges.

[2]

How did you do?

Did this page help you?

1a3 marks

The 500 m tall Taipei 101 tower is shown in Fig. 2.1. The tower has a massive sphere suspended across five floors near the top of the building to dampen down movement of the tower in high winds and earthquakes. The sphere is connected to pistons (not shown) which drive oil through small holes providing damping. The vibration energy of the sphere is converted to thermal energy.

q2-paper-3-june-2018-ocr-a-level-physics
Fig. 2.1 Fig. 2.2

 

Fig. 2.2 models the damper system as the sphere held between two springs. The movement of the walls of the tower forces the sphere to oscillate in simple harmonic motion.

In the strongest wind, the natural frequency of the oscillations of the tower is 0.15 Hz and the maximum acceleration of the sphere is 0.050 m s−2.

a)
Calculate the maximum displacement of the sphere in the strongest wind.





maximum displacement = ....................................... m [3]

How did you do?

1b2 marks
b)
Explain why the natural frequency of the damper system must be about 0.15 Hz.

[2]

How did you do?

1c5 marks
c)
The acceleration a of the sphere is given by the equation

a space equals space minus open parentheses k over m close parentheses x

where k is the force constant of the spring combination, x is the displacement of the sphere and m is the mass of the sphere.

The mass of the sphere is 6.6 × 105 kg. The natural frequency of the oscillations of the sphere
is 0.15 Hz.

i)
Show that the force constant k of the spring combination is about 6 × 105 N m−1.

[3]

ii)
The S-wave of an earthquake causes a sudden movement of the building displacing the sphere 0.71 m from its equilibrium position relative to the building.

Use your answer in (i) to calculate the energy transferred to the springs of the damper system.




energy transferred = ........................................... J [2]

How did you do?

Did this page help you?