A LevelPhysicsOCRExam Questions5. Newtonian World & Astrophysics5.5 Simple Harmonic Oscillations

Simple Harmonic Oscillations (OCR A Level Physics)

Exam Questions

41 mins8 questions

Select a question set to download for
5.5 Simple Harmonic Oscillations

Select an answer set to view for
5.5 Simple Harmonic Oscillations

Medium
Hard
1a3 marks

A long wooden cylinder is placed into a liquid and it floats as shown.

q22-paper-1-nov-2020-ocr-a-level-physics

The length of the cylinder below the liquid level is 15 cm.

a)
i)
State Archimedes’ principle.

[1]

ii)
The pressure exerted by the liquid alone on the bottom of the cylinder is 1.9 × 103 Pa.

Calculate the density ρ of the liquid.




ρ = .............................................. kg m–3 [2]

How did you do?

1b7 marks
b)
The cylinder is pushed down into the liquid and then allowed to oscillate freely.
The graph of displacement x against time t is shown below.

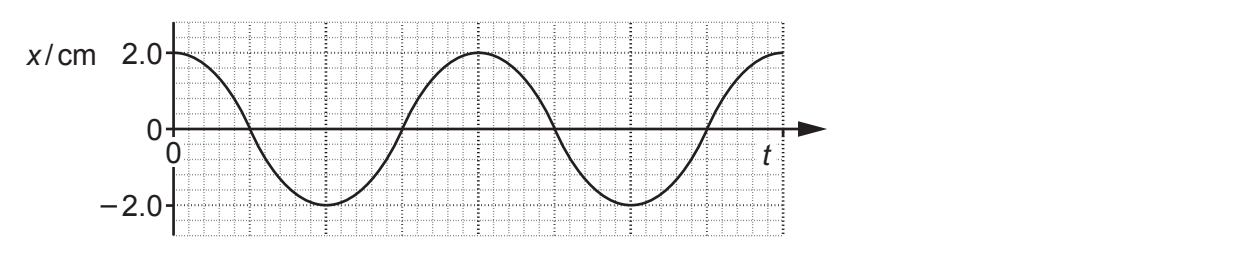
q22b-paper-1-nov-2020-ocr-a-level-physics

The cylinder oscillates with simple harmonic motion with frequency of 1.4 Hz.

i)
Calculate the displacement, in cm, at time t = 0.60 s.





displacement = .................................... cm [3]

ii)
Calculate the maximum speed of the oscillating cylinder.




maximum speed = .................................... m s–1 [2]

iii)
The cylinder is now pushed down further into the liquid before being released.

As before, the cylinder oscillates with simple harmonic motion.

State the effect this has on

1    the amplitude

      ....................................................................................................................

2    the period.

      ....................................................................................................................

[2]

How did you do?

Did this page help you?

1a4 marks
a)
One end of a spring is fixed to a support.
 
A toy car, which is on a smooth horizontal track, is pushed against the free end of the spring.
 
The spring compresses. The car is then released. The car accelerates to the right until the spring returns back to its original length.
 
q21a-paper-1-nov-2021-ocr-a-level-physics

 

The car moves with simple harmonic motion as the spring returns to its original length.
The acceleration of the car is given by the expression a = negative open parentheses k over m close parentheses space straight x, where m is the mass of the car, k is the force constant of the spring and x is the compression of the spring.

Use the data below to calculate the time t it takes for the spring to return to its original length after the car is released.

• mass of car m = 80 g
• force constant k of the spring = 60 N m–1.

t = ....................................................... s [4]

How did you do?

1b7 marks
b)
The arrangement in (a) is used to propel the toy car along a smooth track.

q21b-paper-1-nov-2021-ocr-a-level-physics

i)
Point A is at the top of the track.
 
The launch speed of the car is now adjusted until the car just reaches A with zero speed. The height of A is 0.20 m above the horizontal section of the track.
 
All the elastic potential energy of the spring is transferred to gravitational potential energy of the car.
 
Calculate the initial compression x of the spring.

x = ...................................................... m [3]

ii)
At a specific speed, the car leaves point A horizontally and lands on the track at point B.

The horizontal distance between A and B is D.

q21b-iii-paper-1-nov-2021-ocr-a-level-physics

Air resistance has a negligible effect on the motion of the car between A and B.

1
Explain how the time of flight between A and B depends on the speed of the car at A.

[2]

2
Explain how the distance D depends on the speed of the car at A.

[2]

How did you do?

Did this page help you?

2a5 marks

This question is about a simple pendulum made from a length of string attached to a mass (bob).
For oscillations of small amplitude, the acceleration a of the pendulum bob is related to its displacement x by the expression

a equals negative open parentheses g over L close parentheses x

where g is the acceleration of free fall and L is the length of the pendulum.
The pendulum bob oscillates with simple harmonic motion.

a)
i)
Show that the period T of the oscillations is given by the expression

T squared equals fraction numerator 4 straight pi squared over denominator g end fraction L.

[3]

ii)
A student notices that the amplitude of each oscillation decreases over time.

Explain this observation and state what effect this may have on T.

[2]

How did you do?

2b6 marks
b*)
Describe with the aid of a labelled diagram how an experiment can be conducted and how the data can be analysed to test the validity of the equation  T squared equals fraction numerator 4 straight pi squared over denominator g end fraction L  for oscillations of small amplitude.

[6]

How did you do?

2c4 marks
c)
Another student conducts a similar experiment in the laboratory to investigate the small amplitude oscillations of a pendulum of a mechanical clock. Each ‘tick’ of the clock corresponds to half a period.

i)
Show that the length of the pendulum required for a tick of 1.0 s is about 1 m.

[2]

ii)
If the pendulum clock were to be used on the Moon, explain whether this clock would run on time compared with an identical clock on the Earth.

[2]

How did you do?

Did this page help you?