A LevelPhysicsOCRExam Questions5. Newtonian World & Astrophysics5.4 Circular Motion

Circular Motion (OCR A Level Physics)

Exam Questions

48 mins9 questions

Select a question set to download for
5.4 Circular Motion

Select an answer set to view for
5.4 Circular Motion

Medium
Hard
1a8 marks
a)
A particle-accelerator uses a ring of electromagnets to keep protons moving continuously in a circle. The speed v of the protons depends on the frequency f of rotation of the protons in the circular orbit.
 
Fig. 22 shows data points plotted on a v against f grid.
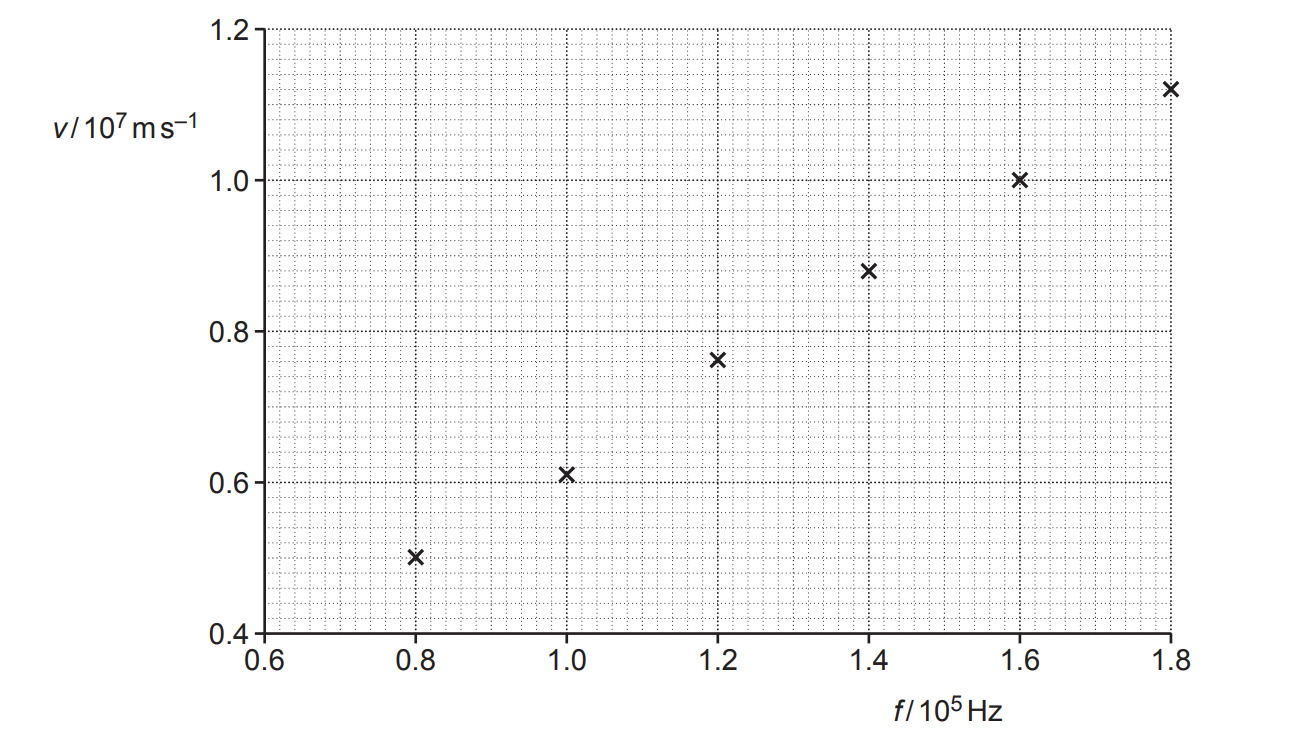
q22a-paper-1-nov-2021-ocr-a-level-physics

Fig. 22

i)
Show that the gradient of the graph of v against f is equal to 2πr, where r is the radius of the circular path of the protons.

[2]

ii)
Show that r is about 10 m by determining the gradient of the line of best fit through the data points in Fig. 22.

[3]

iii)
The maximum speed of the protons from this accelerator is 2.0 × 107 m s–1.
 
Calculate the maximum centripetal force F acting on a proton at this speed.
• mass of proton = 1.7 × 10–27 kg.


F = ...................................................... N [3]

How did you do?

1b2 marks
b)
A new particle-accelerator is now built for moving the protons in a circle of a radius 20 m.

The ring of electromagnets for this new accelerator provides the same maximum centripetal force as the accelerator in (a).

Calculate the maximum speed of the protons in this new accelerator.

maximum speed = ................................................ m s–1 [2]

How did you do?

Did this page help you?

2a3 marks

At an airport, the conveyor belt for suitcases moves at a constant speed of 1.5ms–1.

In Fig. 4.1, a suitcase of mass 8.0kg has reached the line labelled XX'.

q4-paper-3-june-2019-ocr-a-level-physics

Fig. 4.1

Fig. 4.2 shows the situation in vertical cross-section.
The frictional force F prevents the suitcase of weight W from sliding to the bottom of the belt.
The normal contact force on the suitcase is R.
The belt is inclined at an angle of 30° to the horizontal.

q4-2-paper-3-june-2019-ocr-a-level-physics

Fig. 4.2 (not to scale)

a)
By using a vector triangle, or by resolving forces, calculate the magnitude of forces F and R.

F = ............................................. N
R = ............................................. N

[3]

How did you do?

2b6 marks
b)
Fig. 4.3 shows the suitcase and the forces acting on it at the line labelled YY'.

q4-b-paper-3-june-2019-ocr-a-level-physics

Fig. 4.3

The centre of mass of the suitcase is now moving at 1.5 ms–1 along a semi-circular arc of radius 2.0 m.

i)
Calculate the magnitude of the centripetal force acting on the suitcase.

centripetal force = ........................................ N  [2]

ii)
When the suitcase is at line YY', the magnitude of force F is larger and the magnitude of force R is smaller than at XX'.

Explain why this is so.

[4]

How did you do?

Did this page help you?

3a2 marks

Fig. 21 shows the drum of a washing machine.

q21-paper-1-june-2018-ocr-a-level-physics

Fig. 21

The clothes inside the drum are spun in a vertical circular motion in a clockwise direction.

a)
When the drum is at rest, the weight of the clothes is equal to the normal contact force on the clothes at point A.

Explain why these two forces are not an example of Newton’s Third Law of motion.
[2]

How did you do?

3b3 marks
b)
The drum has diameter 0.50 m. The manufacturer of the washing machine claims that the drum spins at 1600 ± 100 revolutions per minute.
 
Calculate the speed of rotation of the drum and the absolute uncertainty in this value.

 
speed = ................ ± ................ m s−1 [3]

How did you do?

3c3 marks
c)
The washing machine is switched off and the speed of the drum slowly decreases. The clothes at the top of the drum at point B start to drop off at a certain speed v.

At this speed v, the normal contact force on the clothes is zero.

Calculate the speed v.


v = ................................................ m s−1 [3]

How did you do?

Did this page help you?

1a3 marks

A small object of mass m is placed on a rotating horizontal metal disc at a distance r from the centre of the disc.

q20-paper-1-nov-2020-ocr-a-level-physics

The frequency of rotation is adjusted using a motor attached to the disc.

The frequency of rotation of the disc is slowly increased from zero, until the object slips off. At this point, the friction F acting on the object is equal to the centripetal force.

The friction F is given by the expression F = kmg, where k is a constant and g is the acceleration of free fall. The constant k has no units.

a)
Show that the frequency f at which the object slips off is given by the equation f squared equals open parentheses fraction numerator g k over denominator 4 pi squared end fraction close parentheses cross times 1 over r.

[3]

How did you do?

1b4 marks
b)
A student plots a graph of lg(f /Hz) against lg(r /m).
q20b-paper-1-nov-2020-ocr-a-level-physics

For this graph: y-intercept = 1 half cross times l g open parentheses fraction numerator g k over denominator 4 straight pi squared end fraction close parentheses

Use the graph to determine the constant k. Write your answer to 2 significant figures.

k = .............................................. [4]

How did you do?

Did this page help you?

2a1 mark

The London Eye, shown rotating anticlockwise in Fig. 6.1, is a giant wheel which rotates slowly at a constant speed.

q6-paper-3-nov-2021-ocr-a-level-physics
Fig. 6.1 Fig. 6.2

 
Tourists stand in pods around the circumference of the wheel.

The floor remains horizontal at all times.

At time t = 0, a tourist who has a weight W of 650 N enters a pod at the bottom of the wheel.

Fig. 6.2 shows the forces acting on the tourist at a later time, when the angle between the pod’s position and the centre of the wheel is 40° above the horizontal. R is the normal contact force and F is friction.

a)
The resultant upward force (R – W) on the tourist changes during the 30 minutes of the rotation of the London Eye as shown in Fig. 6.3.

q6a-paper-3-nov-2021-ocr-a-level-physics

Fig. 6.3

Explain how the graph in Fig. 6.3 shows that the magnitude of the centripetal force on the tourist during the rotation is 0.050 N.

[1]

How did you do?

2b6 marks
b)
i)
Explain why the horizontal force F between the floor and the tourist is necessary.

[2]

ii)
Draw on Fig. 6.3 the variation of the horizontal force F during the 30 minutes of the anticlockwise rotation of the London Eye. Take forces to the right to be positive.

[2]

iii)
Calculate the magnitude of force F when the pod is at the position shown in Fig. 6.2, at 40° above the horizontal.




F = ..................................................... N [2]

How did you do?

2c3 marks
c)
Calculate the distance d of the centre of mass of the tourist from the centre of rotation of the London Eye.





d = ..................................................... m [3]

How did you do?

Did this page help you?