A LevelPhysicsOCRExam Questions3. Forces & Motion3.6 Work, Energy & Power

Work, Energy & Power (OCR A Level Physics)

Exam Questions

54 mins15 questions

Select a question set to download for
3.6 Work, Energy & Power

Select an answer set to view for
3.6 Work, Energy & Power

Medium
Hard
1a2 marks

Fig. 16 shows a hydraulic jack used to lift a car which has a mass of 1200 kg. A mechanic exerts a downwards force of 400 N on the handle of the jack, moving it 80.0 cm downwards. As he moves the handle, the car rises 2.0 cm.

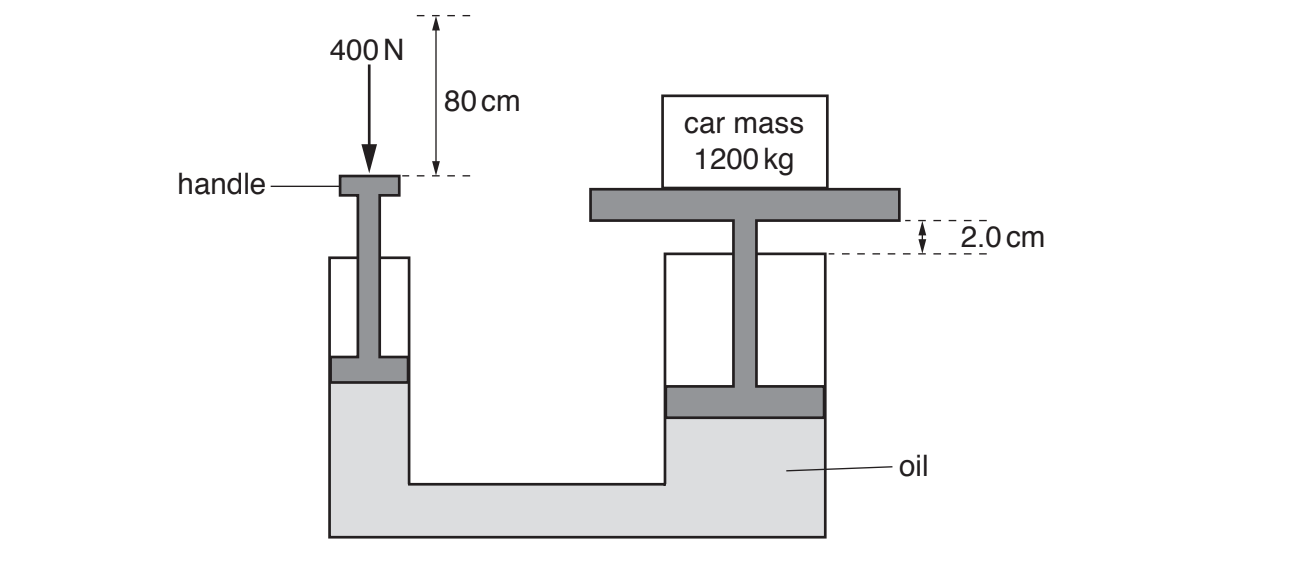
q16-paper-1-june-2017-ocr-a-level-physics

Fig. 16

a)
Calculate the work done by the 400 N force exerted by the mechanic.




work done = ................................... J [2]

How did you do?

1b2 marks
b)
Calculate the ratio fraction numerator speed space of space handle space moving space down space space over denominator speed space of space car space moving space up end fraction.




ratio = .................................. [2]

How did you do?

1c2 marks
c)
Calculate the useful work done on the car and hence the percentage efficiency of the jack.




efficiency = ..................................... % [2]

How did you do?

Did this page help you?

2a2 marks

Wind turbines convert the kinetic energy of the wind into electrical energy.

Fig. 18 shows a wind turbine.

q18-paper-1-june-2018-ocr-a-level-physics
Fig. 18

a)
When the wind speed is 8.0 m s−1, the kinetic energy of the air incident at the turbine per second is 1.2 MJ s−1.
 
Calculate the mass of the air incident at the turbine per second.


mass per second = ............................................... kg s−1 [2]

How did you do?

2b7 marks
b)
A group of engineers are investigating the design of wind turbines.
 
The maximum input power P from the wind is given by the equation
 

P space equals space 1 half rho A v to the power of italic 3

where A is the area swept out by the rotating blades, t is the density of air and v is the speed of the wind.

 

i)
Show that the equation is homogeneous with both sides of the equation having the same base units.

[3]

ii)
The input power to the wind turbine is 1.2 MW when the wind speed is 8.0 m s−1.
 
The density of air is 1.3 kg m−3.
 
Calculate the length L of the turbine blades.


L = ..................................................... m [2]

 

iii)
A wind farm is required to produce an output power of 50 MW when the average wind speed is 8.0 m s−1. The efficiency of each wind turbine is 42%.
 
Calculate the minimum number N of wind turbines required to meet this demand.

N = ......................................................... [2]

How did you do?

Did this page help you?

3a2 marks

Fig. 4.1 shows an arrangement used by a student to determine the acceleration of free fall.

q4-paper-3-june-2018-ocr-a-level-physics

Fig. 4.1

A trolley is attached to a variable mass m by a string which passes over a pulley.

The mass m is released from rest and falls through a fixed height of 0.600 m accelerating the trolley of mass 0.800 kg. When the mass m hits the floor, the trolley then continues to move at a constant velocity v.

This constant velocity v is determined by measuring the time t for the card of length 0.200 m to pass fully through a light gate connected to a timer.

Frictional forces on the trolley and the falling mass m are negligible.

a)
Show that the relationship between v and m is

v squared equals fraction numerator 1.20 space m space g over denominator open parentheses m plus 0.800 close parentheses end fraction

where g is the acceleration of free fall.

[2]

How did you do?

3b4 marks
b)
The student records the information from the experiment in a table. The column headings and just the last row for m = 0.600 kg from this table are shown below.

m/kg t/10-3 s fraction numerator m over denominator open parentheses m plus 0.800 close parentheses end fraction v/m s-1 v2/m2s-2
         
0.600 90 ± 2 0.429 2.22 ± 0.05  

   

i)
Complete the missing value of v2 in the table including the absolute uncertainty.

[2]

ii)
Fig. 4.2 shows some of the data points plotted by the student. Plot the missing data for m = 0.600 kg on Fig. 4.2 and draw the straight line of best fit. 

[2]

q4b-paper-3-june-2018-ocr-a-level-physics

Fig. 4.2

How did you do?

3c5 marks
c)
i)
Use the equation given in (a) to show that the gradient of the graph of v2 against fraction numerator m over denominator open parentheses m plus 0.800 close parentheses end fraction is equal to 1.20 g.

[1]

ii)
Assume that the best-fit straight line through the data points gives 9.5 m s–2 for the experimental value of g. Draw a worst-fit line through the data points on Fig. 4.2 and determine the absolute uncertainty in the value for g.






absolute uncertainty = ± .................... m s−2 [4]

How did you do?

3d4 marks
d)
It is suspected that the card on the trolley did not pass at right angles through the light beam.

Discuss, without doing any calculations, the effect this may have on the experimental value for the acceleration of free fall g.

[4]

How did you do?

Did this page help you?

1a8 marks

Fig. 1 shows a high-speed electric train.

q1-paper-3-nov-2021-ocr-a-level-physics

Fig. 1

The potential difference between the overhead cable and the rails on the ground is 25 kV.  The sliding contact on the top of the train constantly touches the overhead cable.

The overhead cable supplies a current I to the electric motor of the train. The motor turns the wheels.

The train experiences a resultant forward force F.

The total mass of the train is 2.1 × 105 kg.

a)
The train accelerates from rest. The value of F is 190 kN for speeds less than 6.0 m s–1.

i)
Show that the train’s acceleration is about 1 m s–2.

[1]

ii)
Calculate the distance s that the train travels to reach a speed of 6.0 m s–1.



s = ..................................................... m [2]

iii)
The speed of the train is v.
 
During one period of its journey, the train accelerates from v = 30 m s–1 to v = 60 m s–1.
 
The graph of F against v for this period is shown below.

q1a-iii-paper-3-nov-2021-ocr-a-level-physics

1.
Use the graph to show that output power of the electric motor during this period is constant at about 4 MW.

[3]

2.
Calculate the current I in the electric motor when the train is travelling at 50 m s–1.



I = ...................................................... A [2]

How did you do?

1b5 marks
b)
The overhead cable in Fig. 1 must be tensioned.
It is constructed from several equal lengths of wire.

Some data for one length of this wire are shown below.

•    length = 1500 m
•    area of cross-section = 1.1 × 10–4 m2
•    resistivity = 1.8 × 10–8 Ω m
•    the Young modulus = 1.2 × 1010 Pa
•    strain = 1.3%

i)
Calculate the resistance R of one length of wire.




R = ..................................................... Ω [2]

ii)
Calculate the tension T in one length of wire.





T = ..................................................... N [3]

How did you do?

Did this page help you?