Half-Life (OCR A Level Physics) : Revision Note
Half-Life
Half life is defined as:
The time taken for the initial number of nuclei to reduce by half
This means when a time equal to the half-life has passed, the activity of the sample will also half
This is because activity is proportional to the number of undecayed nuclei, A ∝ N

When a time equal to the half-life passes, the activity falls by half, when two half-lives pass, the activity falls by another half (which is a quarter of the initial value)
Determining the Half-Life of an Isotope
To find an expression for half-life, start with the equation for exponential decay:
N = N0e–λt
Where:
N = number of nuclei remaining in a sample
N0 = the initial number of undecayed nuclei (when t = 0)
λ = decay constant (s-1)
t = time interval (s)
When time t is equal to the half-life t½, the activity N of the sample will be half of its original value, so N = ½ N0
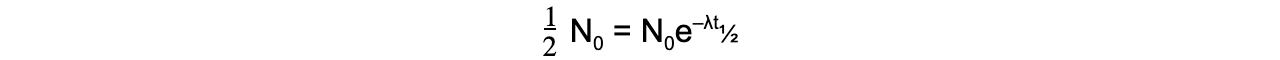
The formula can then be derived as follows:
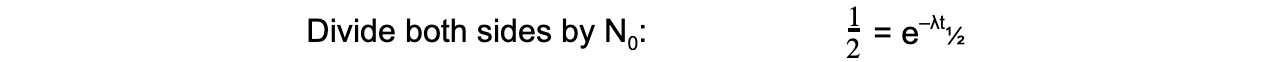


Therefore, half-life t½ can be calculated using the equation:
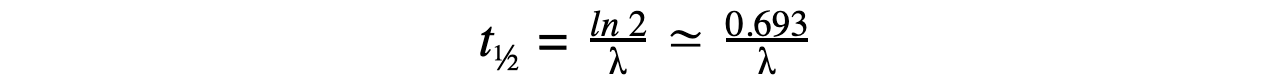
This equation shows that half-life t½ and the radioactive decay rate constant λ are inversely proportional
Therefore, the shorter the half-life, the larger the decay constant and the faster the decay
Worked Example
Strontium-90 is a radioactive isotope with a half-life of 28.0 years. A sample of Strontium-90 has an activity of 6.4 × 109 Bq. Calculate the decay constant λ, in s–1, of Strontium-90.
Answer:
Step 1: Convert the half-life into seconds
28 years = 28 × 365 × 24 × 60 × 60 = 8.83 × 108 s
Step 2: Write the equation for half-life
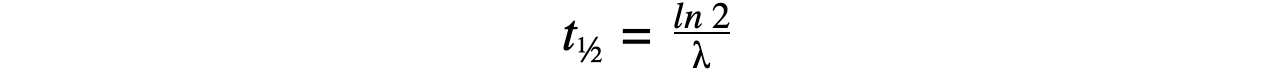
Step 3: Rearrange for λ and calculate
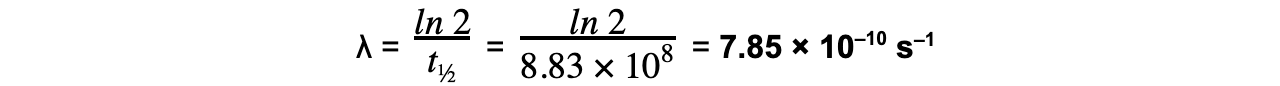
Examiner Tips and Tricks
Make sure you are confident with the meanings of all the definitions and symbols in this unit. It is easy to get confused when completing an examination question.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
