Activity & The Decay Constant (OCR A Level Physics)

• Since radioactive decay is spontaneous and random, it is useful to consider the average number of nuclei which are expected to decay per unit time
  • This is known as the average decay rate

• As a result, each radioactive element can be assigned a decay constant
• The decay constant λ is defined as:

The probability, per second, that a given nucleus will decay

• When a sample is highly radioactive, this means the number of decays per unit time is very high
  • This suggests it has a high level of activity

• Activity, or the number of decays per unit time can be calculated using:

• Where:
  • A = activity of the sample (Bq)
  • ΔN = number of decayed nuclei
  • Δt = time interval (s)
  • λ = decay constant (s^-1)
  • N = number of nuclei remaining in a sample

• The activity of a sample is measured in Becquerels (Bq)
  • An activity of 1 Bq is equal to one decay per second, or 1 s^-1

• This equation shows:
  • The greater the decay constant, the greater the activity of the sample
  • The activity depends on the number of undecayed nuclei remaining in the sample
  • The minus sign indicates that the number of nuclei remaining decreases with time - however, for calculations it can be omitted

Part (a)

Step 1: Write down the known quantities

• • • Mass = 5.1 μg = 5.1 × 10^-6 g
    • Molecular mass of americium = 241
    • N_A = Avogadro constant

Step 2: Write down the equation relating number of nuclei, mass and molecular mass

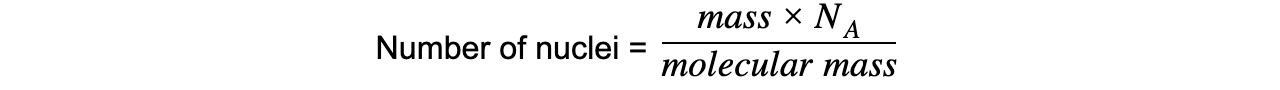
Step 3: Calculate the number of nuclei

Part (b)

Step 1: Write the equation for activity

Activity, A = λN

Step 2: Rearrange for decay constant λ and calculate the answer