Quarks in Particle Decay Equations (OCR A Level Physics): Revision Note
Exam code: H556
Balancing Quark transformation equations
By looking at the transformation of quarks inside the protons and neutrons in beta decay it is possible to analyse the decay of specific quarks inside
Beta-minus decay
In beta-minus decay, one of the neutrons in a nucleus is converted into a proton in a process that may be written as:
n → p + e- +
The neutron, n has the quark composition udd
The proton, p has the quark composition uud
So the beta-minus decay must involve a down quark converting to an up quark
d → u + e- +

Balancing Charge
The charge on the left side of the equation is -
e
The total charge on the right side is
e + (-1)e + 0 = -
e
So, the decay equation is balanced in terms of charge
Beta-plus Decay
In beta-plus decay a proton is converted into a neutron with the emission of a positron and an electron neutrino in a process that may be written as:
p → n + e+ + ve
The proton, p has the quark composition uud
The neutron, n has the quark composition udd
So, the beta-plus decay must involve an up quark converting to a down quark
u → d + e+ + ve

Balancing Charge
The charge on the left side of the equation is +
e
The total charge on the right side is -
e + e + 0 = +
e
So the decay equation is balanced in terms of charge
Charge must be conserved in any reaction or decay equation
Worked Example
The equation for β– decay is
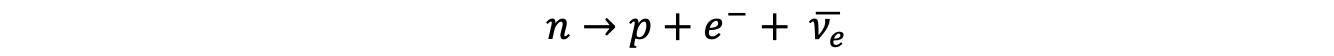
Using the quark model of beta decay, prove that the charge is conserved in this equation.
Answer:


Unlock more, it's free!
Did this page help you?